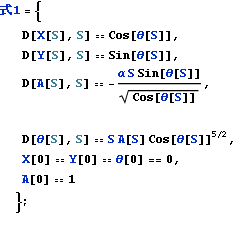
Mathematicaによる大空間へ水平に吹き出す非等温気流の軌道計算
芦村昌士 公開 初回 2013年4月10日
最終 2013年4月14日
はじめに
文献1) 大空間へ水平に吹き出す非等温気流の解析 窪田英樹
空気調和・衛生工学 第47巻 第６号
から
室温が一様かあるいは高さ方向に直線的に分布している大きい空間に
水平に吹き出された冷（温）風の 軌道座標に関して
気流の中心軸に沿う座標sを置換した座標S
水平方向の座標xを置換した座標X
垂直方向の座標yを置換した座標Y
を用いて
以下の連立常微分方程式、式1を得る
上記、式1を数値解法することにより気流の軌道を計算することができる。
文献1)においても、数値解法することにより気流の軌道が計算できることが示されており、
上記、式１に対応するのは、文献１）の式(19)および式(25)である。
文献１）の式(19)においては
,
,
,
の４つの連立微分方程式
文献1）の式(25)においては
,
,
,
の４つの連立微分方程式
であることに対して、上記、式1では
X,Y,A,θの４つの連立微分方程式になっている。
上記、式1の
・・・式(1.a)
が文献1) の式(15)から導かれること、すなわち
上記、式1が文献1) の式(19)および式(25)と同値であることは後述する。
筆者は2007年に同様の検討をしていたが、式(1.b)においてケアレスミスで
としていたが、これは誤りであった。
文献2) 大空間における上下温度分布予測モデル （その２）非等温噴流の評価
三浦 克弘・戸河里敏・他
日本建築学会大会学術講演梗概集(中国)1990年10月
においても
y方向運動量,x方向運動量,x座標,y座標の４つの連立微分方程式になっている。
α -> 0.1
式1においてαを0 .1 として解いて見る。以下の如く式1に代入して式1’を得る
以下の如く、式1’からＳが0から解析域Sの範囲の数値解、解1を得る
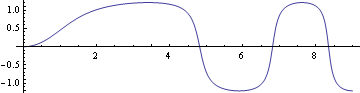
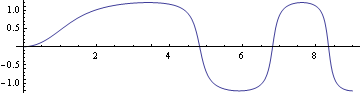
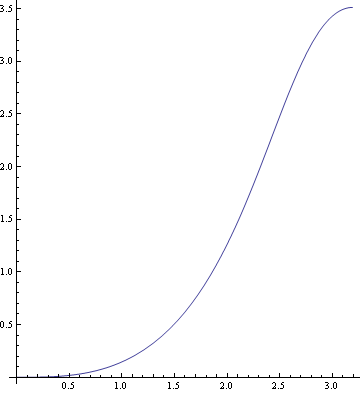
以下の如く、数値解、解1から軌道を描画する。
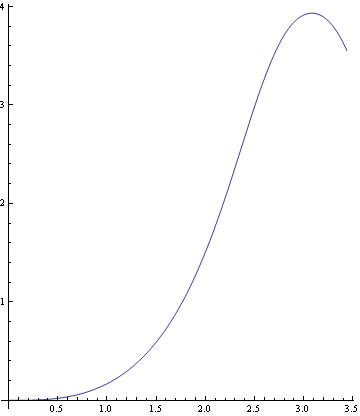
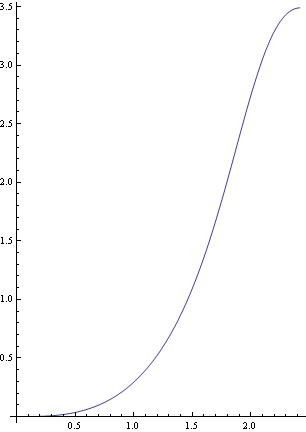
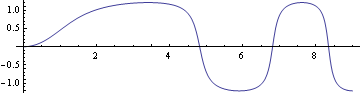
軌道が水平、すなわちθ[S]=0 となる点が噴流の終着端なので、上図のような終着端以降の軌道には物理的には意味はない。
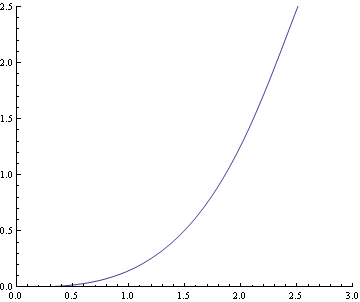
終着端θ[S]=0を近似的に求める為の参考に横軸にSをとってθ[S]を以下にグラフ化した
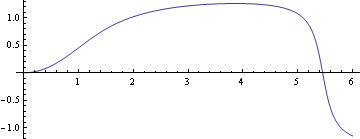
以下の如く、θ[S]=θ[終端S]=0となる軌道が水平、すなわち噴流の終着端のS=終端Sを近似的に求める。
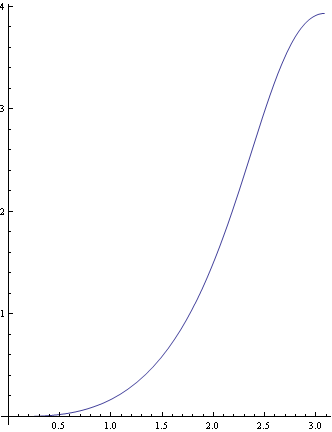
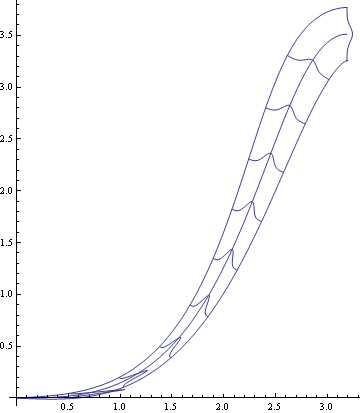
上手のごとく、置換された水平、垂直の座標X,Yにおける、水平に吹き出された周囲より暖かい噴流の軌道が求められる。これは
文献1) 大空間へ水平に吹き出す非等温気流の解析 窪田英樹
空気調和・衛生工学 第47巻 第６号
に示す結果と一致する。
式1の式(1.a)、式(1.b)の誘導
A[s]=1-α 
とすると
文献1)の式(15)から
=
S A[S] ・・・式(1.a)
ここで
=Tan[θ[S]] だから
より
=
式(a) 
=
S A[S] だから
=
S A[S]
置換座標X,Yにおける解1をx,yにおける解1sに変換する
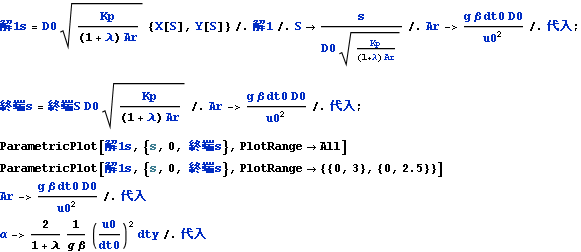
置換座標X,Y,Sにおける軌道は、先の式１にみるようにαの値でほぼ決まってしまう。
文献1)より
α=
dty
dty:周囲空間の温度勾配
である。
文献2) 大空間における上下温度分布予測モデル （その２）非等温噴流の評価
三浦 克弘・戸河里敏・他
日本建築学会大会学術講演梗概集(中国)1990年10月
を参考に以下の代入値をとる
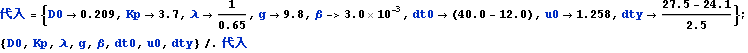
以下の如く、式1’からＳが0から解析域Sの範囲の数値解、解1を得る
以下の如く、θ[S]=θ[終端S]=0となる軌道が水平、すなわち噴流の終着端のS=終端Sを近似的に求める。
MathematicaのFindRootを使う場合、通常、上の２式の前者で問題はないが、本ケースでは例えば後者のようでないと解を得らない。
上の２式で使われている、関数θ[S]が数値解由来であることも作用しているかも知れない。
前者の範囲でも下のような、素朴な方法なら解が得られる。
上を利用してFindRootを用いると
これより文献1)の式(11)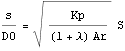 
から置換座標Sの値である終端Sから座標sでの値、終端sを求める
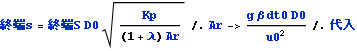
同様に、置換座標X,Y,Sによる軌道の解、解1から座標x,y,sによる軌道の解、解1sを得る
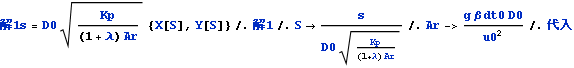
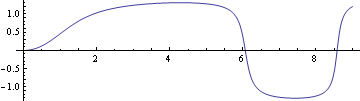
以下の如く、数値解、解1sから軌道を描画する。
文献2) 大空間における上下温度分布予測モデル （その２）非等温噴流の評価
三浦 克弘・戸河里敏・他
日本建築学会大会学術講演梗概集(中国)1990年10月
の実験模型３ｍ×３ｍ 高さ2..5mに合うように上記、軌道を描画し直す
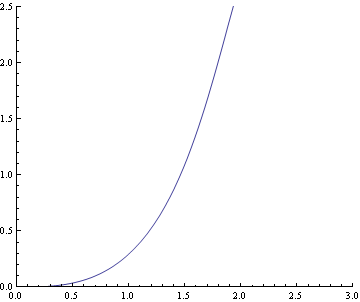
この解析の方がやや軌道の上昇が急激のようである。
文献2)によればこの時、Ar=0.062 から0.037で
本解析では
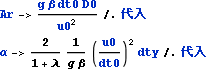
なので、u0を1.4倍して再解析すると以下となる。
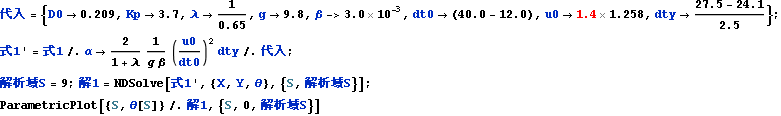
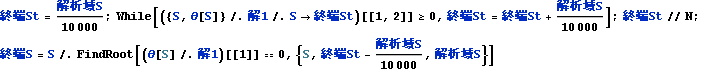
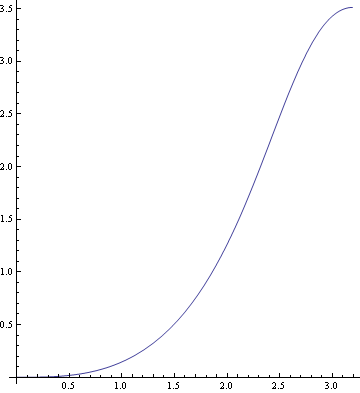
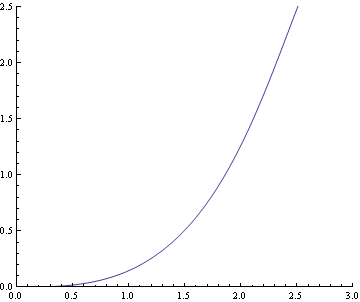
このように
文献2) 大空間における上下温度分布予測モデル （その２）非等温噴流の評価
三浦 克弘・戸河里敏・他
日本建築学会大会学術講演梗概集(中国)1990年10月
の模型実験の結果と、Arの値を実験に合わせることで、本数値解析軌道が比較的良く一致する。
速度分布を描画する
気流軸座標sにおける気流の中心風速umは気流軸置換座標Sにおける置換風速Uから求めることができる。置換風速Uは
文献1) 大空間へ水平に吹き出す非等温気流の解析 窪田英樹
空気調和・衛生工学 第47巻 第６号
の式(13)
Cos[θ]=1
によりSにおけるθから求まる
において
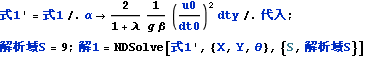
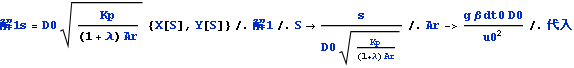
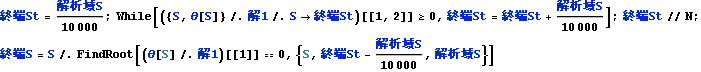
SにおけるUは以下のように求めることができる。
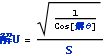
Sにおけるumは
文献1) 大空間へ水平に吹き出す非等温気流の解析 窪田英樹
空気調和・衛生工学 第47巻 第６号
の式(11)
=
から以下のように求めることができる。
このように、物理的に意味のない終端以降でumを求めると風速が上昇する矛盾する結果となる。
また上および下の結果のように、吹き出し口付近でumを求めるとu0より大きくなってしまう。
これは解析解上、S=0で吹き出し口の口径がゼロになっているからである。
実際をより正確に解析する為には、式１の連立常微分方程式の初期条件を実際の吹き出し口径に合わせて工夫する必要がある。
文献2) 大空間における上下温度分布予測モデル （その２）非等温噴流の評価
三浦 克弘・戸河里敏・他
日本建築学会大会学術講演梗概集(中国)1990年10月
の実験模型との噴流軌道との違いは、この影響も少なくないと思われる。
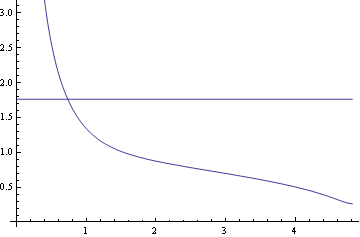
横軸をSに、縦軸にumをとりグラフ化する。
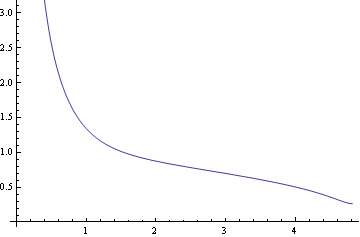
上の如く吹き出し口からS<問題近傍S,でum>u0となっている。
置換されたSにおける問題近傍Sからsにおける問題近傍sを求める
同様に終端sを求める
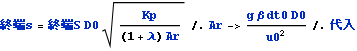
置換されたSではなくsからumを求める。
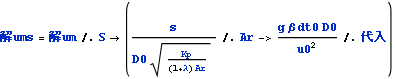
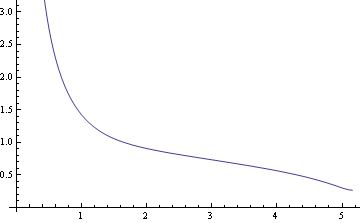
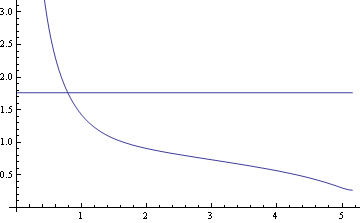
上の如く吹き出し口からs<問題近傍s,でum>u0となっている
次に解umsを用いてSにおける風速の分布、解uを求める
文献1) 大空間へ水平に吹き出す非等温気流の解析 窪田英樹
空気調和・衛生工学 第47巻 第６号
の式(1)
から以下のように求めることができる
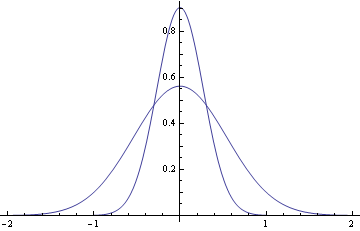
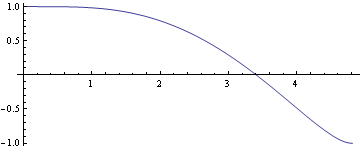
以下のように、Sにおいてθを与える解、解θから、sにおいてθを与える解、解θｓ を求める。
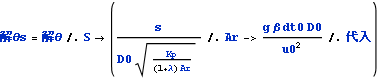
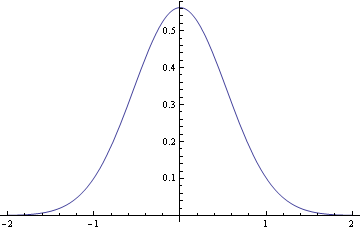
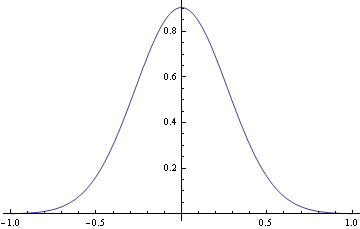
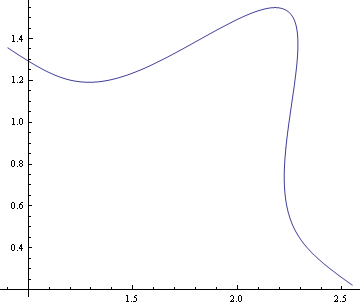
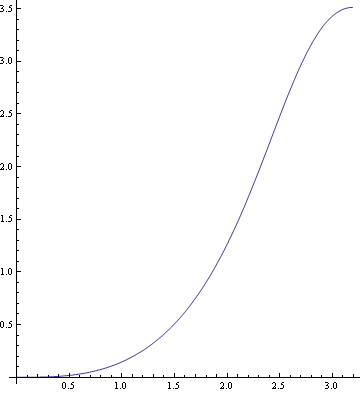
以下にs=st において、風速分布を軌道の傾きに合わせた描画を試みる
気流の温度分布を計算する
文献1) 大空間へ水平に吹き出す非等温気流の解析 窪田英樹
空気調和・衛生工学 第47巻 第６号
の式(12)から
=T[s] 
式(15)から
=
S A[S]
ゆえに
T[S] 
=
S A[S] から
T[S] =
を得
解 A[S]からT[S]の解を得ることができる。そのため、これまでは
解析域S = 6; 解1 = NDSolve[式1’, {X, Y, θ}, {S, 解析域S}]
としてきたが、Aの解を得る為
解析域S = 6; 解1 = NDSolve[式1’, {X, Y, θ,A}, {S, 解析域S}]
とする。
において
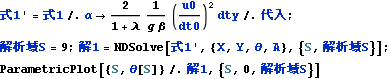
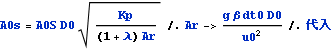
T[S] =
より
以下に
文献1) 大空間へ水平に吹き出す非等温気流の解析 窪田英樹
空気調和・衛生工学 第47巻 第６号
の図-4(b
にならって
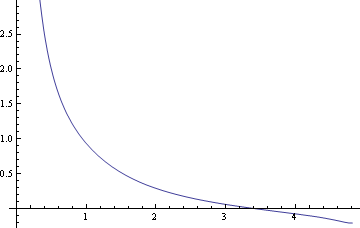
横軸に気流軌道の高さ方向置換Y軸、縦軸に解Tのグラフを描く
以下に
文献1) 大空間へ水平に吹き出す非等温気流の解析 窪田英樹
空気調和・衛生工学 第47巻 第６号
の図-4(b
にならって
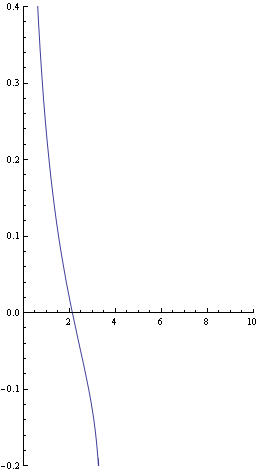
横軸に気流軌道の高さ方向y軸、縦軸に気流の周囲静止空気との温度差・解dtmsのグラフを描く
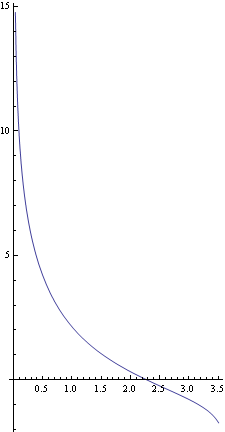
まとめ
文献1) 大空間へ水平に吹き出す非等温気流の解析 窪田英樹
空気調和・衛生工学 第47巻 第６号
の式(12)(13)(14)(15)
はX,Y,T,Uに関する微分をS,θ,に関連ずける方程式であり、これを数値解析するものであった。
また
文献2) 大空間における上下温度分布予測モデル （その２）非等温噴流の評価
三浦 克弘・戸河里敏・他
日本建築学会大会学術講演梗概集(中国)1990年10月
においては、
x,y,θ,um,tmに関する微分を関連ずける方程式であり、これを数値解析するものであった。
これに対して、本稿は、式1
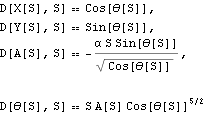
において、X,Y,θ,Aの微分をS,θ,に関連ずける方程式であり、これを数値解析するものになっている。
文献1)におけるT,U、文献2)におけるum,tmは解析の目的として重要な変数であり
その物理的意味も明快である。
これに対して本稿の
A[s]=1-α 
の物理的意味は比較的間接的である。
T[S]の解を得るにA[s]の解を必要としたが、
を求める必要はない。
今回、本稿のこの連立常微分方程式・式1が、Mathematicaを用いて数値計算できることを示した。
