
計算幾何学
文献1)コンピュータ・ジオメトリ 計算機幾何学:アルゴリズムと応用 第3版 P54による
穴のある非凸多角形の単調な多角形への分割 Mathematicaによる実装
穴のある非凸多角形の三角形分割への為に
以下のように単調な多角形に分割したい、穴のある非凸多角形のデータを作成する。
データは1つの外殻と2つの穴、処理図形穴1、処理図形穴2として作成した。
必要性があってのことだが、後ほど図示するように、外殻は反時計まわり、穴は時計まわりに、頂点の座標を定義した。
このアルゴリズムを三角形分割の前段階とするとき、この段階で穴の問題が解決されている。
In[1]:=

以下のように、穴のデータは反時計まわりに定義したものをReverse組み込み関数を使って、時計まわりのデータに変換している。
In[2]:=
![]()
In[3]:=
![]()
1つの外殻と2つの穴、処理図形穴1、処理図形穴2を以下のようにまとめて処理図形とした。
In[4]:=
![]()
このノートブックを利用するユーザーが用意するのは、ここまでである。後以下は、私の解説文とユーザが造ったデータとで内容が異なるだろうがMathematicaが全て自動的に処理する。
この処理図形は以下のように描画できる
In[5]:=
![]()
Out[6]=
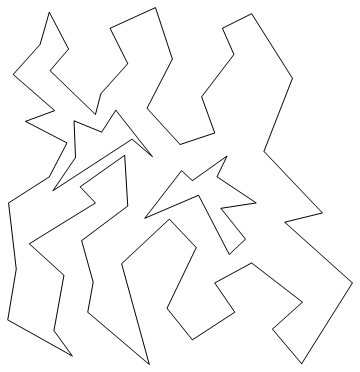
外殻の頂点の数は53個、処理図形穴1の頂点の数は10個,処理図形穴2の頂点の数は7個である。
In[7]:=
![]()
Out[7]=
![]()
外殻、処理図形穴1、処理図形穴2あわせて70個の頂点となる。外殻、処理図形穴1、処理図形穴2は閉じた多角形(閉曲図形)なので、外殻、処理図形穴1、処理図形穴2あわせて70個の辺を持つ。まず、この70個の辺のデータ頂点辺リストdを作る。外殻、処理図形穴1、処理図形穴2あわせて70個の頂点に1から70の通し番号をふるものとし、通し番号nの頂点を始点する辺を通し番号nの辺とする。繰り返すと
外殻の最初の頂点通し番号を1、最後の頂点通し番号を53
処理図形穴1の最初の頂点通し番号を54、最後の頂点通し番号を63
処理図形穴2の最初の頂点通し番号を64、最後の頂点通し番号を70
と処理図形の全70頂点に1から70の通し番号をつけて、70個のデータ、頂点辺リストdをつくる。
この頂点辺リストdの通し番号1のデータは{{53,1,2},{-0.7551,0.8967},{-0.8043,0.7248}}となる。
この{53,1,2}の1が通し番号1の辺のデータであるとともに、その始点が通し番号1の頂点であることを示している。{53,1,2}の2がこの辺の終点が通し番号2の頂点であることを示している。{53,1,2}の53は、この辺の始点に通し番号53の辺が接続していることを示している。{53,1,2}は、時計まわり、反時計まわりに応じた、隣あった3つの頂点の通し番号の並びを表してもいる。{53,1,2}は1番目の辺の始点に53番目の辺が、1番目の辺の終点に2番目の辺が接続しているとも読め、しばしば、この読み方の方が重要となる。
{-0.7551,0.8967}はこの辺の始点の座標、{-0.8043,0.7248}は終点の座標である。
以下のようにして、処理図形={外殻,処理図形穴1,処理図形穴2}からこの頂点辺リストdを生成している。
ここで使われる通し番号は、辺のそれと、頂点のそれであったりするが、本アルゴリズムにおいては、辺の通し番号の方がしばしば重要で、頂点はn番目の辺の始点とかで議論されることの方が多い。n番目の頂点という記述もするが、本アルゴリズムにおいては、そのとき必ずn番目の辺が存在し、その始点がn番目の頂点である。
In[8]:=

Out[10]=
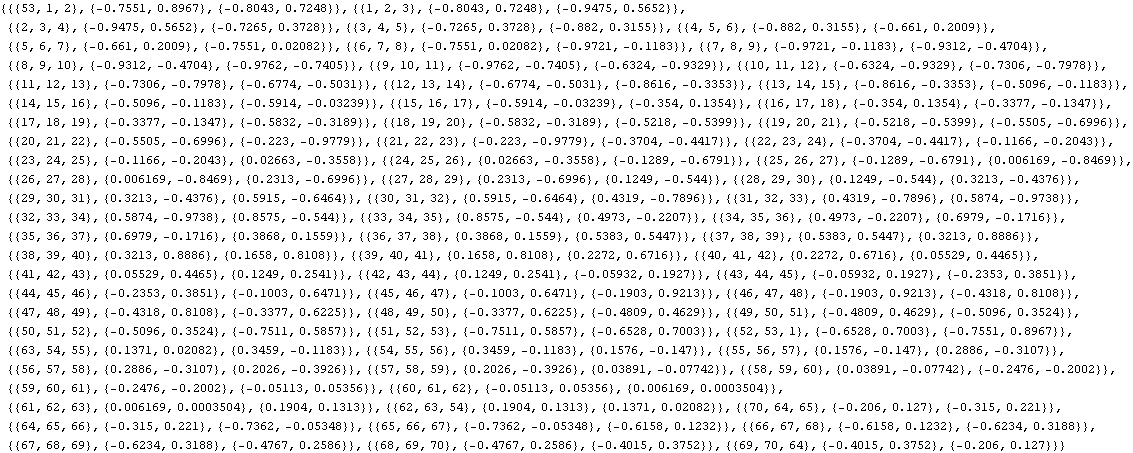
頂点辺リストdの通し番号1のデータ、すなわち通し番号1の頂点と通し番号2の頂点を結ぶ通し番号1の辺のデータは{{53,1,2},{-0.7551,0.8967},{-0.8043,0.7248}}であったがこれから
通し番号1の辺のデータが{{53,1,2},{-0.7551,0.8967},{-0.8043,0.7248},{1}}と負荷情報{1}がついたデータを持った頂点辺リストというものを作る。何故{1}付加されているかと言うと、通し番号1の頂点のy座標が通し番号2の頂点のy座標よりも大きいからである。これは通し番号1の辺が下向きであることを示してもいる。文献1)のアルゴリズムでは後述するがヘルパー点という概念が重要となる。実はこの負荷情報{1}は頂点1(通し番号1の頂点)が辺1(通し番号1の辺)のヘルパー点であることを示す。とりあえず辺の始点、終点のうち上にあるものを(Y座標値が大きい)をヘルパー点としている訳である。以下で、このようにヘルパー点を初期化設定しつつ、この頂点辺リストを生成している。このヘルパー点を表す{1}は例えば操作アルゴリズムにおいて{1,5,7}となったり{1,5}となったり、動的に変化するものである。{1,5,7}の場合、通し番号7の頂点が最新のヘルパー点ということを意味する。{1,5,7}が{1,5}になるときは、最新のヘルパー点が1つ前に戻されたという表現を使っている。
In[11]:=
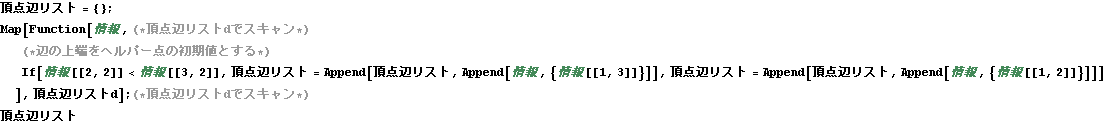
Out[13]=

下のように頂点辺リストにおける通し番号50の辺の情報をみると、頂点の定義が49→50→51であること頂点50と頂点51はどちらが上にあるかというと頂点50(通し番号50の頂点)であって、この辺はヘルパー点が通し番号50の頂点に初期設定され下向きであることが判る。
In[14]:=
![]()
Out[14]=
![]()
この頂点辺リストを用いて以下のように描画することができる。外殻は反時計まわり、穴は時計まわりに、頂点の座標を定義したことが継承されていることが判る。
In[15]:=
![]()
Out[15]=
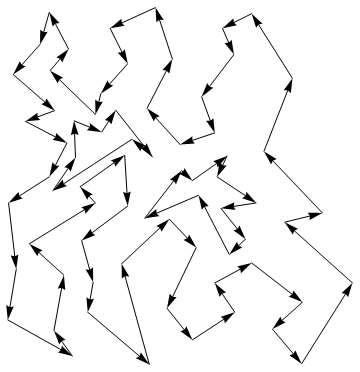
以下のように、頂点辺リストから、出発点、分離点、最終点、統合点を判別する。
頂点辺リストの70個の情報をスキャンしてこれをなしている。
頂点辺リスト[[情報[[1,1]],2]]は対象の辺の始点を終点とする辺の始点の座標
情報[[2]]は対象の辺の始点の座標
頂点辺リスト[[情報[[1,3]],2]]は対象の辺の終点の座標
ゆえに、外積=Append[v1,0]×Append[v2,0]は、対象辺の始点頂点の両側の辺を対象辺の始点から張られたベクトルとしたときの外積を表している。各頂点、各辺は2次元でX-Y平面上にあるので外積はZ座標の成分として現れる。
出発点はまず、その両側の頂点が下にあるのだが、分離点もこの要件を満たすので、これだけでは判定できない。その両側の辺がなす図形内部側の角度が2πより小さいので、外積は負の値となることを利用する。このとき、外殻は反時計まわり、穴は時計まわりに、頂点の座標が定義されていることが必要である。
In[16]:=

このように以下のように、頂点辺リストから、出発点、分離点、最終点、統合点が抽出される
In[18]:=
![]()
Out[18]=
![]()
In[19]:=
![]()
Out[19]=
![]()
In[20]:=
![]()
Out[20]=
![]()
In[21]:=
![]()
Out[21]=
![]()
一般点は全頂点の出発点、分離点、最終点、統合点、以外なので以下となる
In[22]:=
![]()
Out[22]=
![]()
出発点、分離点、最終点、統合点、を図示すると以下となる
In[23]:=

In[27]:=
![]()
Out[28]=
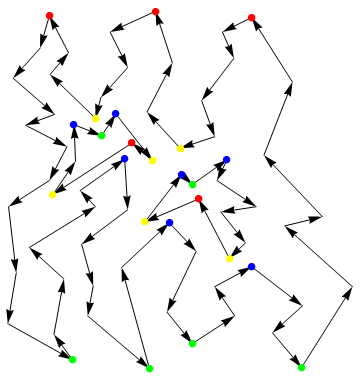
通し番号nの頂点データ=頂点辺リスト[[n]]として
水平交点リスト[通し番号nの頂点データ]という関数を下のように定義する。
これは、通し番号nの頂点の文献1)の言うところのすぐ左側の辺、すぐ右側の辺の情報を返すものである。
頂点辺リストをスキャンして、通し番号nの頂点データと比較検討している。
通し番号nの頂点から水平線を引いたとき、その水平線と交わる辺があるかチェックしている。
走査対象の辺の情報が情報という局所変数名(この水平交点リスト関数内部だけで使われ外部から干渉されない)で処理されている。
局所変数listaに交点があった場合に{交点のある辺のデータ、交点の座標}という形で、水平線と交わる辺のデータが蓄積されていく。ComplementはNullという結果を取り除く為に使われている。
局所変数listaに登録された辺情報を、通し番号nの頂点の左側にあった場合を局所変数listldに、右側にあった場合を局所変数listrdに振り分ける。これらを交点のx座標の大きさで並べかえたのが局所変数listl、listrである。このような手順で、
水平交点リスト[通し番号nの頂点データ]という関数は
{{通し番号nの頂点のすぐ左側の辺情報, 水平線との交点座標},
{通し番号nの頂点のすぐ右側の辺情報, 水平線との交点座標}}を返す。
In[29]:=

例えば通し番号30 の頂点のすぐ左側,右側の辺の情報が 以下のように返される。
In[30]:=
![]()
Out[30]=
![]()
左側の辺の情報は、{頂点辺リストの25番目の頂点辺情報、その交点座標}
In[31]:=
![]()
Out[31]=
![]()
右側の辺の情報は、{頂点辺リストの34番目の頂点辺情報、その交点座標}
In[32]:=
![]()
Out[32]=
![]()
頂点辺リストで、全ての頂点について水平交点リストを実行して見る。
In[33]:=
![]()
Out[33]//MatrixForm=
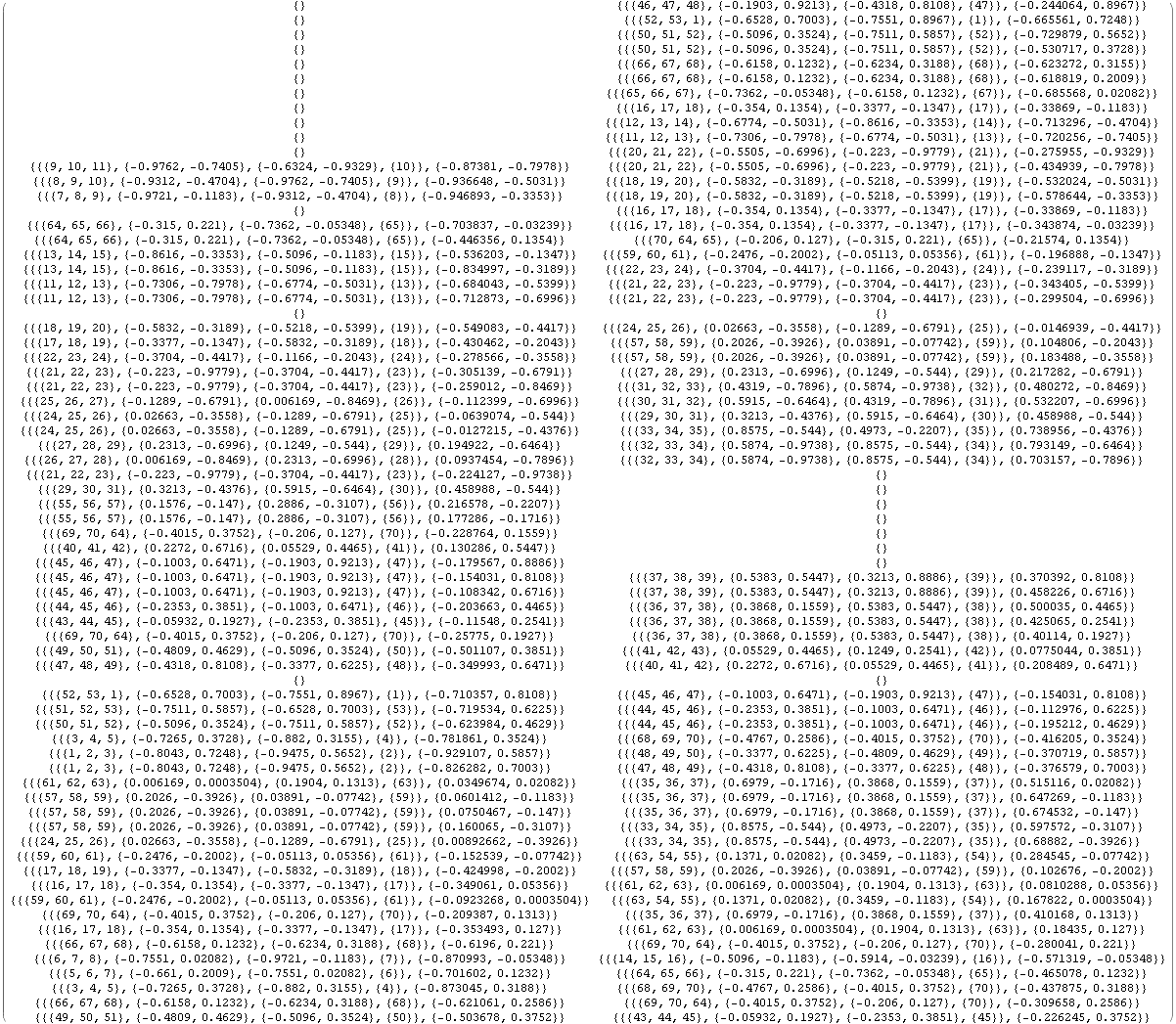
以下のように頂点を上から走査する為、頂点番号をy座標順に上から並び変えたリストy座標順頂点番号リストを作る。その際x座標で先だって並べ変えておく。
In[34]:=
![]()
Out[34]=
![]()
以下に定義した、対角線作成[]を実行すると、穴のある非凸多角形を単調な多角形への分割する為の対角線が返される。
上から下に(Y座標が大きいものから小さいものへと)70個の頂点を走査するために、Mapでy座標順頂点番号リストから局所変数:頂点番号を順次受け取り処理している。
上から下にの走査頂点が一般頂点だった場合、(これより上にある統合点のみが、対角線相手の候補となる)
この頂点を始点とする辺が下向きに定義されている場合は、辺の右側が内部となり
この頂点を終点とする辺の最新ヘルパー点を調べる。
最新ヘルパー点が統合点だった場合は、この頂点と、ヘルパ点を結ぶ線が対角線となり、最新のヘルパー点はひとつ前に戻される。
この頂点を始点とする辺が上向きに定義されている場合は、辺の左側が内部となり
この頂点を始点とする辺のすぐ左側の辺の最新ヘルパー点を調べる。
ヘルパー点が統合点だった場合は、この頂点と、ヘルパ点を結ぶ線が対角線となり、最新のヘルパー点はひとつ前に戻される。
上から下にの走査頂点が分離頂点だった場合、(すぐ左の辺の最新ヘルパー点が統合点であるか、すぐ左の辺の上端が候補)
すぐ左の辺の最新のヘルパー点を調べる
最新ヘルパー点が統合点だった場合は、この頂点と、最新ヘルパ点を結ぶ線が対角線となり、最新のヘルパー点はひとつ前に戻される。
そうでない場合は、この頂点と、すぐ左の辺の上端を結ぶ線が対角線となる。(最新ヘルパー点をひつつ前にもどすことはない)
上から下にの走査頂点が統合頂点だった場合、
すぐ左の辺の最新のヘルパー点として、この統合頂点を加える。
In[35]:=

上で定義した対角線作成[] を実行すると、以下のように結果が対角線リストに代入される。
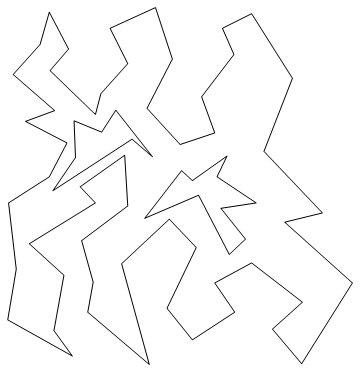
対角線は以下のように描画され、これにより穴のある非凸多角形が単調な多角形に分割されていることが確認できる。
In[36]:=
![]()
Out[36]=
![]()
In[37]:=
![]()
Out[37]=
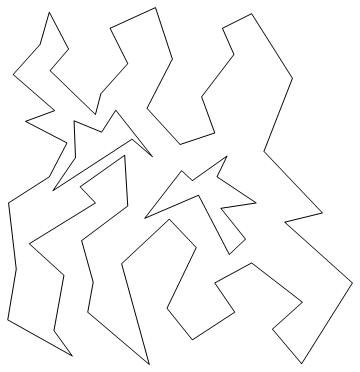
In[38]:=
![]()
Out[38]=
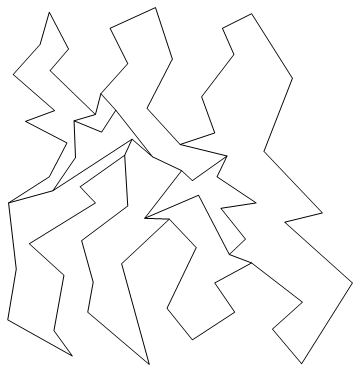
単調多角形への分割対象は複数の穴があるにしても、ただ1つの外殻を持つ図形であった。1つの対角線は外殻を持つ図形を1つ増やすと見なせる。それに伴い、新たに辺を2つ増やすと考えると処理しやすい。さらに、対角線に接続することになった、既存2つの辺の接続辺番号を変える。対角線の両端を始点とする既存2本の辺の始点に接続する辺の情報を変える。1つの対角線が生成する新たな2辺の情報は互いに始点と終点が入れ換わっている。
これまで頂点辺リストのn番目の辺データにおいて頂点辺リスト[[n]][1,2]=n であったが新頂点辺リストにあっては、もはやこれは必ずしも成立しない。すなわちn番目の辺の開始点はn番目の頂点とは限らない。と言うのは対角線によって新たに辺が加えられても、辺の属性として参照する頂点の通し番号は旧番号を参照しているからだ。
In[39]:=

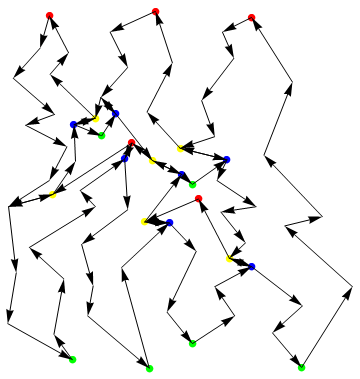
新頂点辺リストを用いれば対角線が以下のように描画される。対角線は双方向の矢印となり、2つの辺が重なっていることが見てとれる。
In[42]:=
![]()
Out[42]=
In[43]:=
![]()
Out[43]=
In[44]:=
![]()
Out[44]=
![]()
この例では穴のある非凸多角形を単調な多角形に分割する為に8本の対角線を要した。ゆえに新頂点辺リストは頂点辺リストに較べて、その2倍の数の16本辺が増えている。
この新頂点辺リストから各辺を各分割された単調多角形に振り分けていく。すなわち単調多角形リストを作成していく。処理済み辺番号リストを動的に作成して、これが空{}になるまで振り分け操作を行うものとする
In[45]:=

In[48]:=
![]()
Out[48]=
![]()
In[49]:=
![]()
Out[49]=
![]()
In[50]:=
![]()
Out[50]=
![]()
7つの単調多角形に分割されている。描画しやすいように、これを座標のリストに変換する。
In[51]:=

Out[51]=

In[52]:=

Out[53]=
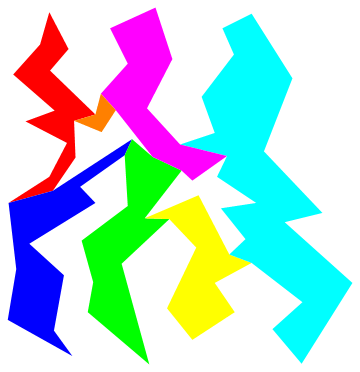
In[54]:=
![]()
Out[54]=

以上のように、穴のある非凸多角形が単調な多角形に分割される。本アルゴリズムは文献1)を参照して実装したものであるが、文献1)は、より少ない試行回数、より小さいメモリーでこれを成すことを重視していると思われる。この点、本アルゴリズムは全くこれを配慮していない。文献1)は、地球上の地図情報などを計算幾何学によって処理することを念頭に入れているように思われる。筆者は、これを主に建築分野等における部品等の3Dのデータモデリングに応用することを念頭においていることもあって、本アルゴリズムが全く実用に供さないような、極端に要素が多い場合は想定していない。基本的な分割アルゴリズムの骨格に理論的破綻が無いことを頼って文献1)を参照した。走査を行っている関数:対角線作成[]の中で、これまたスキャンを要する水平交点リスト[頂点]という関数を呼び出していることなど、無駄な多重ループになっているとも思われる。
辺が水平、垂直になっている場合の例外処理なども、恐らくまだ不備であろう。これは今後、改善していく。他、文献1)の指摘する、データの縮退の問題もあろう。改善すべき、改善できるところは、改善して行きたい。改善ができなくはないが相当な困難が予想される場合は、アルゴリズムを利用するユーザのデータの作り方に制限を与えることのトレードオフで考えることもあるだろう。