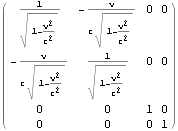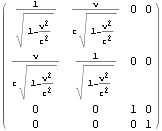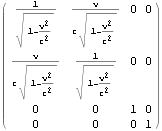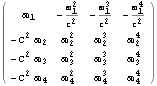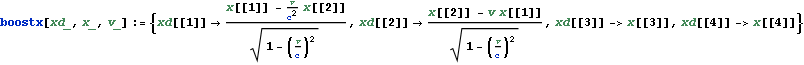
Mathematicaで特殊相対性理論 2013
公開 2014年１月９日 芦村昌士
はじめに
参照文献を以下とする
文献：中野）相対性理論 物理入門コース９ 中野董夫 著 （岩波書店）
文献：パウリ上）相対性理論 上 Ｗ・パウリ著 内山龍雄 訳 （ちくま学芸文庫）
文献：パウリ下）相対性理論 下 Ｗ・パウリ著 内山龍雄 訳 （ちくま学芸文庫）
文献：アインシュタイン選集 １）アインシュタイン選集1 湯川秀樹監修 （共立出版）
文献：ディラック）一般性相対性理論 P.A.Mディラック 著 江沢 洋 訳 （ちくま学芸文庫）
文献：ジンマーマン）物理学のためのMathematica -古典力学から宇宙論まで- ロバート・ジンマーマン/フレデリック・オルネス 著 武藤 覚/小泉 悟 訳 （ピアソン）
文献：EMAN）EMANの物理学 http://homepage2.nifty.com/eman/index.html EMANの物理学 http://homepage2.nifty.com/eman/relativity/contents.html 相対性理論 http://homepage2.nifty.com/eman/relativity/variant.html 反変ベクトル・共変ベクトル
http://homepage2.nifty.com/eman/relativity/increase.html 増大する質量
相対性理論について書かれた本を読んで、それが理解できるかどうかは、もしその本に誤植があったとして、それに気づけるかどうかと、無関係ではあるまい。そして、それはその本で省略されている数式（数の式ではなく数学の式）の変形等の過程があったとして、自分でも正しく数式を変形・計算して、本と同じ結論記述に到達できるかと無関係ではない。以下では、その操作の多くをMatmaticaの数式処理関数Simplify等に追わせている。それは本稿筆者自身の能力ではなくてMathematicaの能力を利用しているのではあるが、Mathematicaを正しく使う能力と合わさって、他者の要請に従って、相対性理論上の問題を正しく解く能力を間接的に得たことに準じよう。
他者の要請に従って、相対性理論上の問題を正しく解く能力があることが、相対性理論を正しく完全に理解していることと同値ではないかも知れないが、相対性理論を正しく完全に理解しているならば、他者の要請に従って、相対性理論上の問題を正しく解くことができるとは言えよう。
本稿は、少なくとも、他者の要請に従って、相対性理論上の問題を正しく解ける可能性があることを、Mathematicaを利用してはいるものの、本稿の読み手と共有せんとするものである。これが、広く、相対性理論を正しく完全に理解することの普及に貢献することを願う。
本稿筆者は、相対性理論を数式を用いずに説明するの類は、少なからず不毛の結果をもたらすと考える。
数式を扱うことを苦にして、相対性理論を理解する努力を敬遠するのであれば、Mathematicaを用いて、その敬遠を回避することも、また有意義かと思う。
Mathematicaでの記述を全て開示することは、記述が正しいにしろ、正しくないにしろ、極めて、あいまいさが無い、ということにおいて非常に優れている。説明図を描くにしても、そのMathematicaでの記述を全て開示すれば、どうして、どのようにして、その図が描かれたのか明快になる。第三者がその誤りを指摘する上でも有用な情報となろう。
Mathematicaには数学を処理し、数学の問題を解く能力はあるにしても、相対性理論は知らない直接は扱えないとして、Mathematicaに相対性理論を注入する、代入する、教えるという立場を読者と共有し、Mathematicaに相対性理論の問題を解かせることによって、相対性理論の理解を読者と共有せんとするものである。
本稿は、特殊相対性理論において、質量とエネルギーの等価理論を導出するところを目標とする。本稿筆者にとって、特殊相対性理論のローレンツ収縮、時間遅れ、双子のパラドクスに比して、質量増加、質量とエネルギーの等価理論の理解はより難しい問題であった。本稿筆者はニュートン力学が相対性理論からみて、近似理論でしかない点に注目したかったので、ニュートン力学の範疇でない電磁気学・電気力学の議論を極力さけて理解したいと本稿をまとめた。
しかしながら、文献：パウリ 上）に指摘されているように、電気力学の助けをかりずに、真の特殊相対性理論の理解は難しいと思える。あるいは、電気力学の助けをかりずに、特殊相対性理論の全てをより物議・疑義を持たずして語るのは難しいと思われる。質量増加、質量とエネルギーの等価理論においてそうである。
しかしながら、質量増加の理論を活用すれば、質量とエネルギーの等価理論は、もはや電気力学の助けをかりなくても、ある程度理解できるというのが本稿筆者の感想である。その意味で本稿筆者にとってのボトルネックの１つが質量増加だ。あるいは、やはり根底においては電気力学のたすけを必要としているではあろうが、双曲線運動論から、質量増加を介さず質量とエネルギーの等価理論を示す道もあろうかと思える。
文献：中野）は、本稿筆者にとって、かなり不明確なテキストであった。質量とエネルギーの等価理論を導出するにあたって、明示的に質量増加理論も電気力学の参照も行われないからだ。本稿筆者にすれば、そこに無理があり、難解さに影響しているのではと思わざるを得ない状態だ。
本稿では、質量増加の説明を、文献：パウリ 上）のｐ292のLewisとTolmanの提唱した提案、思考実験の工夫に負っている。その説明は電気力学のたすけをかりない、巧みなものと言えよう。別の言い方をすれば、ある程度、言葉を尽くさないと理解できない、必ずしも自明でないことでもある。文献：中野）は、明示的に質量増加理論も電気力学の参照も行わずに、質量とエネルギーの等価理論を導出しているので、本稿筆者には、そこに、LewisとTolmanの提唱した提案、思考実験の工夫の類が紛れているのではと推察する。とすれば、それを相応な説明も無しに理解するのは容易ならざるものがあると思える。
本稿読者にとって、最大のボトルネックはローレンツ変換であろう。本稿は第一に説明無にこれを用いる。これをもとに、ローレンツ収縮、時間遅れ、速度の加法定理、双子のパラドクス、質量増加、質量とエネルギーの等価理論を導出する。光速度不変も積極的に扱わない。光速度不変の要請がローレンツ変換だからでもある。ニュートン力学の精密性の欠如は正に光速度不変を説明できないことにあり、ローレンツ変換が加えられることが、ニュートン力学の公理体系に代わる、新しい物理学・相対性理論の公理体系と本稿筆者は考える。
ローレンツ変換
ｘ軸に沿った速度{v,0,0}のローレンツ変換を示す。Mathematicaで表記に拘束されない形で定式化すると便利である。
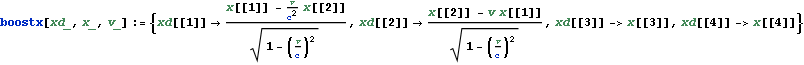
文献：パウリ上）p48 によるものと同じである。文献：パウリ上）p184において
世界点を{ i c t,x,y,z}としたときは
,
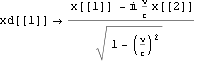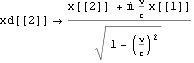世界点を{ c t,x,y,z}としたときは
,
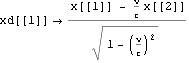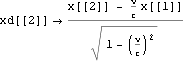である。
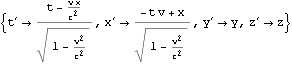
上はK’座標系の座標値{t’,x’,y’,z’}はK座標系の座標値{t,x,y,z}でどう表されるか（観測されるか）、ただしK’座標系は静止座標系とみなすK座標系からみてx軸に沿って速度{v,0,0}で等速運動していると読める。ローレンツ変換によって{t’,x’,y’,z’}は{t,x,y,z}を使ってどう表られるかぐらいに読むと良いかも知れない。
このboostx関数の第一引数xdは結果である等速慣性系Ｋ’座標系における{時間軸座標値、ｘ軸座標値、ｙ軸座標値、ｚ軸座標値}である４次元ベクトルを代入すべき４次元ベクトルの要素の単なる記号・シンボルの情報であり適時状況に応じて{t’,x’,y’,z’}や{dt’,dx’,dy’,dz’}としておけば良い。各ベクトル成分・要素に具体的な数値や数式を与えるべきではない。第二引数xは適時状況に応じて{t,x,y,z}や{dt,dx,dy,dz}ような記号・シンボルの４次元ベクトルを与えても良いし、各ベクトル成分・要素に具体的な数値や数式を与えることもできる。第三引数vは静止系K座標系から見てx軸に沿って等速運動する等速慣性系K’座標系の運動速さであり、vのような記号・シンボルを与えても良いし、具体的な数値や数式を与えることもできる。
本稿で処理の結果を記号に=で代入せず → で置きかえの形にしているのは、後でその記号を使って、別の式を表現するとき、Clear関数とか使って、代入をリセットする手間を省く為である。結果を=で代入するときは、極力、日本文字混じりの変数名に代入する。従って、やたらそうしないようには留意するが、主にアルファベット、ギリシャ文字の変数の意味は、論議の流れで、変わる場合がある。使うアルファベット、ギリシャ文字の数を浪費しない為である。
文献：ジンマーマン）p460 ではboostx関数はローレンツ変換の行列を与える。ただしc=1。本稿では代入式の形とした。
文献：中野）ｐ68 (5.17)に同じ。
文献：パウリ上）ｐ48 (1)に同じ。
逆変換は以下となる。第三引数が-vになっていることに留意。
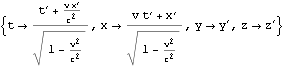
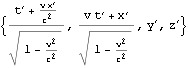
文献：中野）ｐ68 (5.17’)に同じ。
文献：パウリ上）ｐ48 (1.a)に同じ。
以上は{t, x, y, z}に関するものであったが、{T, x, y, z}={c t, x, y, z}に関する場合も用意しておく
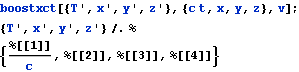
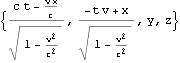
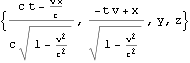
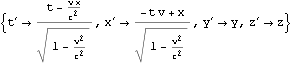
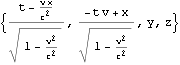
ローレンツ収縮
文献：中野）ｐ78
文献：パウリ上）ｐ49
静止系でx軸の長さＬはK’系では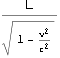
と観測され長くなる。
正確に言うと静止K座標系でx軸に沿って距離Ｌ離れて速度{v,0,0}で走る２つの粒子は、この粒子が静止してみえるK’座標系では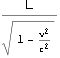
離れた静止した２つの粒子と観測される。
２つの粒子を棒の両端とし、棒の静止状態の長さL0＝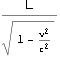
こそが本来の棒の長さとすればL=L0
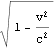となり、等速度運動している長さＬは静止の長さL0より短く、等速度運動している物体の長さのローレンツ収縮となる。(以下Mathematicaによる検算)
検算１
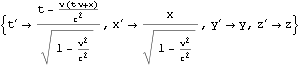
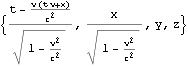
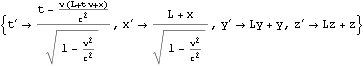
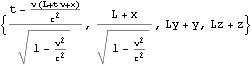
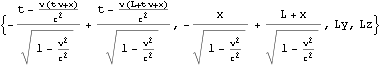
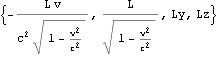
検算１ct
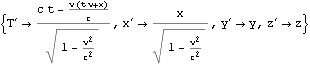
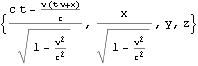
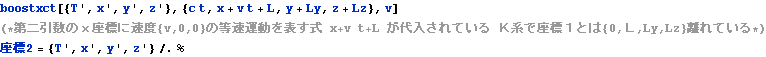
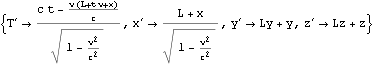
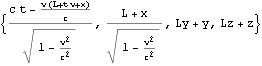
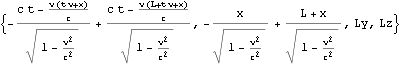
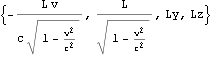
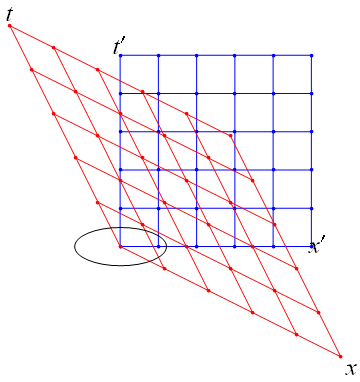
作図1
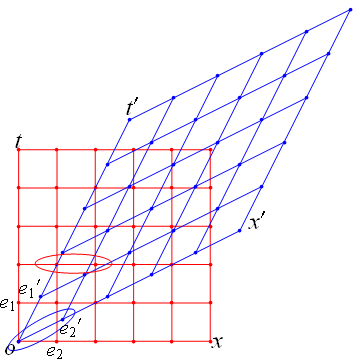
上図、世界線o-t’は座標系K:t-o-x(赤いグリッド)において、x軸に沿う速度{v=0.5,0,0}で等速運動する点のグラフである。同時に世界線o-t’は座標系K’:t’-o-x’(青いグッド)においては、静止点を表す。これはこのローレンツ変換の題意に沿っている。
上図の赤い楕円の中のように、青のx’軸１目盛が赤のx軸１目盛に足らないことが見てとれる。これがローレンツ収縮である。
上図の青い楕円の中のように、赤いx軸１目盛が青のx’軸１目盛に足らないことが見てとれる。これがローレンツ収縮である。
K:t-o-x(赤いグリッド)において座標{t,x,y,z}={
,
,
,
}と表記されることは位置ベクトル{
,
,
,
}が、基底ベクトル
,
·
+
·
+
·
+
·
と表されることでもある。上図のo→
が
、o→ 
が
である。
K’:t’-o-x’(青いグリッド)において座標{t’,x’,y’,z’}={
’,
,
’,
}と表記されることは位置ベクトル{
’,
,
’,
}が、基底ベクトル
,
·
+
·
+
·
+
·
と表されることでもある。上図のo→
が
、o→ 
が
である。
ローレンツ変換{
,
,
,
} → {
’,
,
’,
} に対して、{
,
,
,
}→{
’,
’,
’,
’}はその逆変換になる。すなわち位置ベクトル{
,
,
,
} は反変ベクトルである。このことは、後述する。
上図、作図において、K:t-o-x(赤いグリッド)の格子点を、K’:t’-o-x’(青いグッド)の格子点に変換するに、boostx[{t,x,y,z},{j,i,y’,z’},-v]とboostx[{t,x,y,z},{j,i,y’,z’},v]の逆変換を用いているのは、そのような事情による。
尚、ローレンツ変換{
,
,
,
} → {
’,
,
’,
} に対して、{
,
,
,
}→{
’,
’,
’,
’}はその逆変換になるというのは
ローレンツ変換係数が世界点を{c t,x,y,z}と表す場合の変換係数のように
であることが必要で、世界点を{t,x,y,z}を表す場合の変換係数
はこれを満足しない。上の作図では、格子点の変換にboostxct[{c t,x,y,z},{j,i,y’,z’},-v]ではなくboostx[{t,x,y,z},{j,i,y’,z’},-v]を用いてしまっているが、c=1としていることから、この作図に限っては
が成立している。
本稿筆者は、このように座標系の目盛・格子を計算して描くことが肝要と考える。計算無に目盛の無い定規とコンパスだけで上図を正確に描くことは容易ではない。
文献：中野）ｐ79 図５-9 は同種の図であるが、目盛が無いので判りにくい。図を定規で計測しても正しいローレンツ収縮率は得られないと考える。あくまでも上図のような図上の目盛で読む必要がある。
検算2
以下のMathematicaによる検算は、結果は同じだが、中間結果に物議が生じやすい。
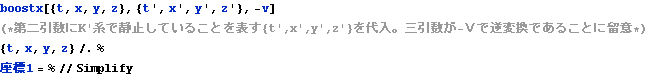
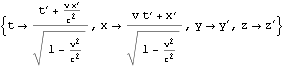
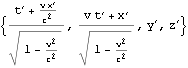
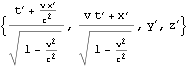
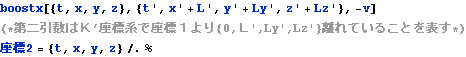
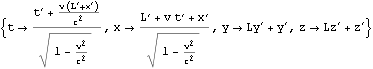
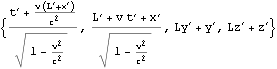
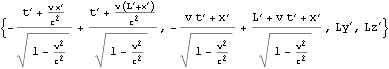
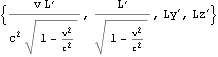
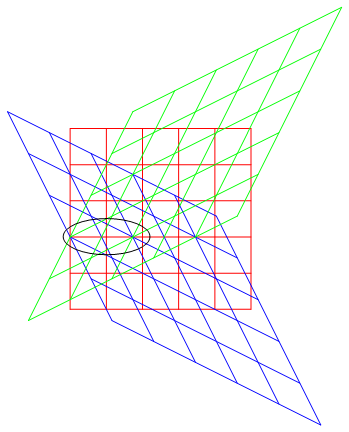
作図2
上図の楕円の中のように、赤のｘ軸１目盛が青のｘ’軸１目盛に足らないことが見てとれる。これがローレンツ収縮である。
本稿筆者は、このように座標系の目盛・グリッドを計算して描くことが肝要と考える。計算無に目盛の無い定規とコンパスだけで上図を正確に描くことは容易ではない。
ローレンツ収縮のアインシュタインの思考実験
上の図は、楕円内において、青色のグリッド２目盛のｘ座標値、緑色のグリッド２目盛のｘ座標値が、赤い色のグリッドｘ座標値２目盛に足りないローレンツ収縮を表している。同時に青色のグリッド２目盛の長さの棒と、緑色のグリッド２目盛の長さの棒とが、反対方向から近づき,重なり合った様をも表し、これが文献：パウリ上）ｐ51に記された、赤色のグリッドでローレンツ収縮を観測する、アインシュタインの思考実験による方法を示している。
速度の加法定理
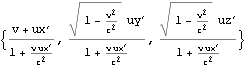
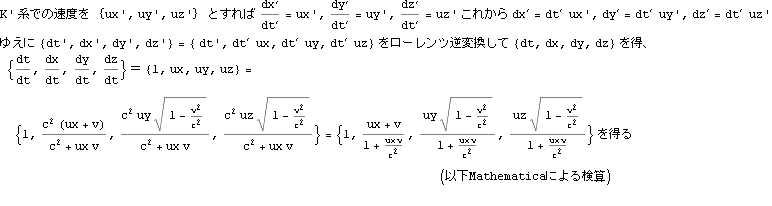
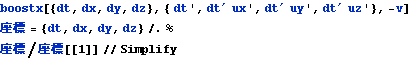
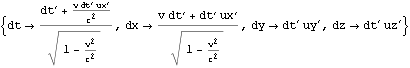
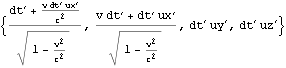
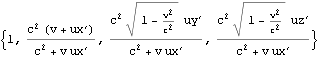
文献：中野）ｐ84
文献：パウリ上）ｐ59
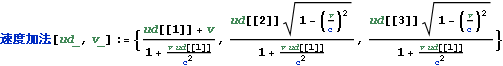
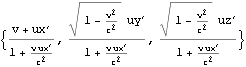
質量増加（横質量 縦質量） LewisとTolmanの提唱した提案、思考実験
空間座標{x,y,z}={0,-L,0}に立つ観測者Ａから見て観測者Ｂは一定速度{v,0,0}でｘ軸に平行に空間座標{x,y,z}={0,L,0}を通過するように走っているとする。
これは空間座標{x’,y’,z’}={0,L,0}に立つ観測者Bから見て観測者Ａは一定速度{-v,0,0}でｘ軸に平行に空間座標{x’,y’,z’}={0,-L,0}を通過するように走っているように見える。
観測者Ａは球Ａ、観測者Ｂは球Ｂを放ち、球Ａと球Ｂは空間座標{x,y,z}={x’,y’,z’}＝{0,0,0}で衝突し跳ね返り、球Ａは観測者Ａに、球Ｂは観測者Ｂに戻るとする。
球Ａと球Ｂの静止質量は等しくm0とする。観測者Ａは球Ａを速度{0,uy,0}={0,-uy’,0}でY軸に平行に投げ、観測者Ｂは球Ｂを速度{0,uy’,0}={0,-uy,0}でY軸に平行に投げる。
この現象が起こるということ自体が、電気力学によらない以上、光速度不変、ローレンツ変換だけからでは導けない、質量の変換法則を導く為の特殊相対性理論の公理が内含されているといえよう。
強いて言えば、
文献：パウリ上）の立場からは
それぞれの球のもつ速度のｘ成分は衝突の前後で不変とする、つまり両球のあいだの運動量の授受の行われる方向はy軸の方向とする
ＡとＢの対象性から、ＡもＢもそれぞれの球の運動を観測するときまったく同じ結果をうるはずである
などとも関係する。
ここで、物体の速度がセロである瞬間というのは球Ａと球Ｂが衝突する瞬間を想定してでのことだが、ここではゼロというのがｙ軸方向だけのことで良いのかという問題もある。
観測者Aから見た球Ｂの衝突後の速度は速度の加法定理から以下となる。
すなわち観測者Ｂから見た球Ｂの座標は
なので、これを速度{-v,0,0}でローレンツ変換して観測者Aから見た球Ｂの座標を得、時刻で除することにより速度を得る。
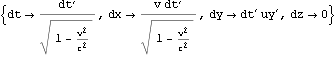
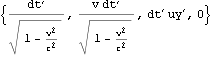
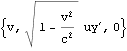
これより以下のようにｙ軸に平行な運動量の保存から、観測者Ａからは球Ｂの質量は以下のmvと観測される。
は後に
→0 の極限をとり、結論することを想定しているので静止質量m0としている。
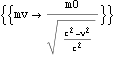
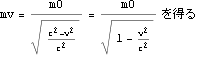
上のmvは速度合成速度uB=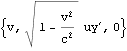
のときの質量ではあるが極限 
→0 でも上式は成立するので 速度{v,0,0}のときの球Ａ、Ｂの質量として差し支えなくなる。すなわち
は観測者Ｂが球を投げだすさずに観測者Ａから見て球Ｂが速度{v,0,0}で走っているときの観測者Ａが観測する球Ｂの質量である。観測者Ａが観測する投げ出された球Ｂの質量は
のvの代わりに観測者Ａの観測する球の合成速度uBから
を代入すれば良い。そして、観測者Ａが観測する投げ出された球Ａの質量、観測者Ｂが観測する投げ出された球Ｂの質量は
のvの代わりにuy=
を代入すれば良い。
文献：パウリ上）ｐ292
この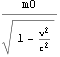
は横質量とも呼ばれる。後述するが、
なる縦質量もある。
静止質量m0の粒子が速度{v,0,0}のとき、この粒子の質量が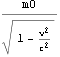
となると解釈できるが、
速度{v[t],0,0}の粒子に加速度{
,0,0}が加えられる場合、その加速力がニュートン力学でmo 
となるに習って、m0を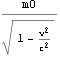
に置き換えて、その加速力を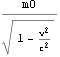
と求めてはならない。正しくは
となるのである。
このことは、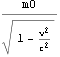
から以下のように導出できる。
ニュートン力学でもそうであるように、力は運動量の時間微分で求める。
すなわち
を時間微分で求めるのである。すると、縦質量が浮かび上がってくる。
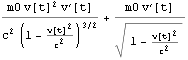
ここで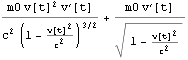
=
(
+
)=
=
=
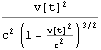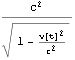このように、力を運動量の時間微分で求めると間違いは起きにくいのであるが、ニュートン力学の 力 = 質量 加速度 で求めると間違いやすい。これはニュートン力学では質量が時間の関数であり得ないのに対して、特殊相対性理論では質量は時間の関数であるvを介して時間の関数であることに起因し、これは文献：EMAN）の増大する質量 で指摘されている。
本稿筆者は、ニュートン力学では通用する、力 = 質量 加速度 の法則を特殊相対性理論では否定してしまって、力=運動量の時間微分 という法則だけを残せば、横質量だけで足り、縦質量は不用かとも考える。
文献 ：パウリ 上）は縦質量は示されるが、明示的にこの議論はない。文献：中野）には質量増加、横質量、縦質量の言及すらない。
本稿筆者は文献：EMAN）の増大する質量 を読むまでこの議論に気がつかず、質量とエネルギーの等価理論に行きつくのに難儀したのである。
運動量 力 エネルギー 質量エネルギー等価理論
あらためて、下に横質量 と速度{v[t],0,0}の積、すなわち運動量の時間微分からの力{f,0,0}のfを示す。
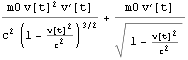
ここで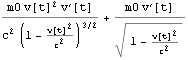
=
(
+
)=
=
=
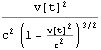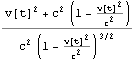
下のように、この力fに速度を乗じると、運動エネルギーの時間微分を得る。これは 文献：パウリ 上）p289 (317) に示される。
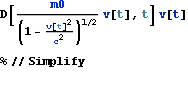
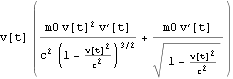
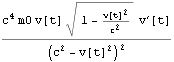
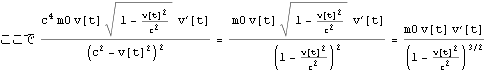
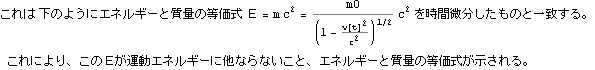
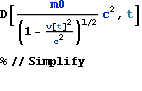
時間の遅れと双子のパラドクス 固有時間τ
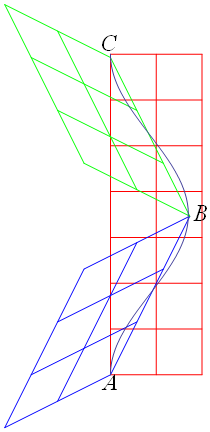
文献：中野）ｐ95 図5-14 に対応、文献：パウリ上）ｐ187 第４図に関連 する図を下に示す。
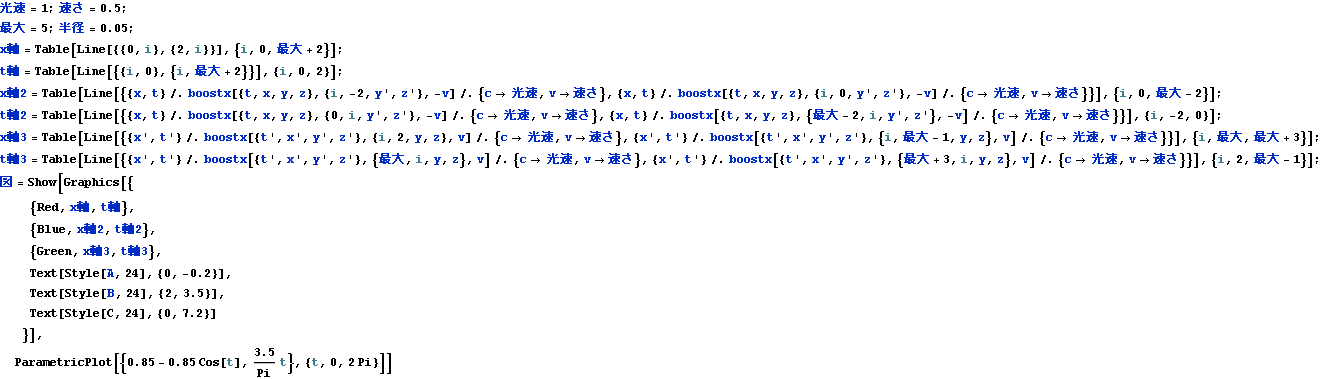
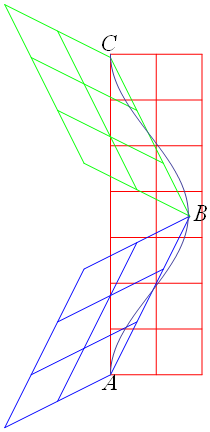
青色の座標グリッドと緑色の座標グリッドが接する点Bが星Ｂでロケットが折り返す （乗り換える） 時空座標点である。
直線ABは往きのロケットを静止系とみる座標系の時間軸、世界線である。
青色の座標グリッドにより往きのロケットの中では星Ｂに到達するのに時間３目盛分経過しているA →B。
緑色の座標グリッドにより還りのロケットの中では地球に到達するのに時間３目盛分経過しているB →C。
直線ＢＣは還りのロケットを静止系とみる座標系の時間軸、世界線である。
ロケットの中で往復に合計６目盛分A → B→C、時間が経過しているが、地球では赤色の座標グリッドのほぼ７目盛分A →C時間が経過している。
ＡＣは地球を静止系とみる座標系の時間軸、世界線である。
本稿筆者の感想では、結論の定性は同じだが、文献：中野）ｐ95 図5-14 では経過時間の差がより大きくとらえらる印象を受ける。
本稿のように座標系の目盛・格子を計算して描き目盛で読むことが肝要と考える。
文献：中野）ｐ95 でもロケットが地球を出発するとき、星Bで折り返すとき、地球に帰還するとき、ロケットは加速度運動するので、
加速度を受けない地球の時計との比較では、特殊相対性理論が適用できないこと、従って双子のパラドクスは生じず、
ロケットで星Bまで旅行した方が若いこと（地球に較べて時間経過が小さい）が示唆される。
加速度を扱う解析になるので、この計算は一般性相対性理論にあずけることになり、
文献：中野）ｐ95 、文献：パウリ上）ｐ54、 ｐ187でもそう示唆される。
しかしながら、文献：パウリ上）ｐ187 によれば、文献：パウリ上）第４図の曲線Lの接線（世界線）が水平に近づくほど（ロケットの速度が速いほど）ロケット内の時計の目盛幅は大きくなり、経過時間は小さくなり、曲線であるがゆえの図示上の見かけの孤の全長が大きくなるに勝って、経過時間は短くなる。従って、地球上の時計の到着予定時刻で目的地に到達するに、一様な速さ（世界線が直線、折れ線の世界線の直線部分）のロケットで出発点を通過してから、目的地を通過するまでのロケット内での経過時間が最も大きくなる。それでも、その経過時間は地球での経過時間よりは短く、ロケットの中の方が若くいられる。それを示しているのが上図である。文献：パウリ上）の説明はまた、地球上の時計の到着予定時刻で目的地に到達するに、地球Aから加速度をもって出発し、加速度をもって星Bに着陸し、また加速度を持って星Bを出発し、加速度を持って地球Cに到達した方がよりロケットの中で若くいられることを示す。さらには、地球上の時計の到着予定時刻で目的地に到達するに、途中で行ったり来たりを繰り返して（世界線が蛇行した曲線）、積極的に加速度を受けた方が、ロケットの中でより若さを保たれることが示唆される。途中でロケットを静止さたり、逆走したりすれば、地球上の時計の到着予定時刻で目的地に到達するに、より大きい加速度でロケットの速さを大きくし直さなければならないことになるからだ。（この本稿筆者の解釈・見解は再検討・議論が必要かもしれない）
参考に上図上にA → B→Cの曲線となるロケットの世界線を描いている。この曲線上に目盛はプロットしていないが、曲線上にその目盛を読んでいくと、６目盛分よりも小さくなりさらにロケット内での時間経過は小さくなり若くいらることになる。
ゆえに、上図および、文献：中野）ｐ95 図5-14 はロケットの中の経過時間は地球に較べて、少なくともこれだけ短い、ロケットの中では若く、いられることを示す。
このように加速度を扱う解析になるので、この計算は一般性相対性理論にあずけることになるのではあるが、文献：パウリ上）ｐ187では、特殊相対性理論の範疇でも、ある程度は説明できることを示している。
本稿筆者は、加速度の効果があるから、双子のパラドクスは無いのを、亜光速で宇宙旅行をしても地球に留まるより相対的に若くなることは無いと誤解していた時期があった、しかし加速度を豊富に経験する宇宙旅行をした方が、より若い状態で双子の兄弟に出会えるので、パラドクスが解消されているのである。
ある程度の説明するに、上図を用いるに、文献：中野）ｐ95 図5-14を用いるに、文献：中野）では、往き専用、還り専用の等速運動するロケットに飛び乗る、飛び移る、飛び降りる、ことを想定して説明している。しかし、双子の片方がロケットに携帯する時計の世界線が上図のようなA → B→C折れ線になることはない。とんがった部分は必ず曲線である。でなければ、双子の片方がロケットの中で無限大の加速度を受けることになるからだ。ロケットに飛び乗ったり、飛び移ったとしたときは、必ずロケットの内壁にぶつかり、内壁から加速度を受け、身体が押しつぶされ歪、この歪がクッションとなって、急激な速度変化が緩和される。上図は、往き還り、それぞれのロケット内の加速度を受けることのない時計の経過時間を合計して、それが地球の時計の経過時間より小さいことを言うが、それは双子の片方がロケットに携帯する時計の経過時間ではない。加速度を受ける双子の片方がロケットに携帯した時計の経過時間の方がさらに小さい。
上図は、青い色のグリッドの時間軸３目盛分の経過が、赤色のグリッドの時間軸３目盛分の経過を越えていることからも、ローレンツ変換における時間の遅れを示している。(以下Mathematicaによる検算)
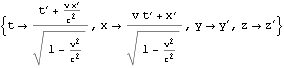
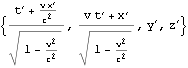
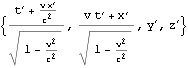
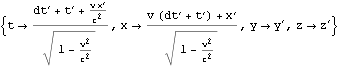
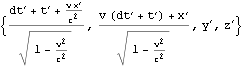
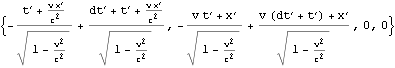
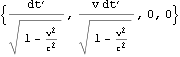
文献：中野）ｐ77
文献：パウリ上）ｐ56
加速度を豊富に経験する宇宙旅行はアンチエイジングに有効である。時空の理論物理学上、相対性理論上そう言える。しかしながら本稿筆者は、地球上での医学的方法によるアンチエイジングと比較してみたい。宇宙旅行中に一生懸命、勉強して地球に還ったとしても、地球に留まって、同じように一生懸命に勉強した人間と較べて、勉強は進んでいないだろう。時間の進みが遅く歳をとらないということは、勉強していた時間も短くしかとれなかったからだ。地球上での医学的方法によるアンチエイジングなら若く見えても歳を取っていて、勉強時間も長くとれていたので、より賢くなれている（はずだ）。
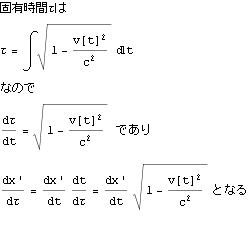
固有時間τ
先ず、直線ＡＢ、直線ＢＣのロケットが等速運動の場合は
τ微分=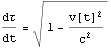
より
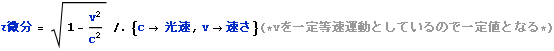
となりA → B → Cにおいて、青色、緑色のグリッド、ロケットの中の時計でほぼ６目盛となっていることが確認できる。
曲線A → B → Cは赤い色のグリッドの時間軸の目盛値がtのとき、ｘ軸の目盛値が0.85-0.85Cos[t]と表される曲線で
となり5.59<6.06でロケットがこのような速さ変化(加速度)をもって宇宙旅行する方が、さらに双子の兄弟の片方がロケット旅行で携帯している時計での経過時間は地球での経過時間よりも短くなる。
それでも、ロケットが動いていることの代わりに、地球を動いているとみなせば、地球に留まっている双子の兄弟の片方のほうが若いことになり、パラドクスは解消していないという主張もあるかも知れないが、この特殊相対性論的、入れ替えが違反で、してはいけないことと言うべきであろう。すなわち、ロケットが慣性系で加速度を受けずに、代わりに地球が加速度を受けるというのが題意に反していると言うべきであろう。地球にいる人間が、ロケットで感じ得るような加速度を感じるという前提が、あり得ない題意に反することなのだ。しかるに、ロケットの加速運動が、重力のような遠隔力だとすれば、ロケットの中の人間は自由落下のエレベータの中にいるように加速度を感じぜすにすみ、その場合なら、地球と立場を入れ替えても差しつかえないかも知れない。しかしながら、その場合は、地球のみならず、月も太陽も、このロケット以外の全宇宙をその遠隔力場加速度系におかねばならず、その物理学的意味が希薄すぎる。全宇宙が自由落下にあるという仮定はそうであっても観測し得ないという意味で想定を否定できないが、ロケットだけが例外というのはおかしい。裏返せば、ロケットの加速運動として、地球などが全くその影響受けないとする遠隔力場を想定することも困難である。
ローレンツ不変
はローレンツ変換で不変である。文献：パウリ上）p70 (以下Mathematicaによる検算)
は
＝
で、
を満たす座標{t,x,y,z}は原点から放射された光速の粒子の座標を表す。
がローレンツ変換で不変なことがMathematicaによって検算されたが、これは光速不変の検算となる。
これを四元計量として関数化しておく
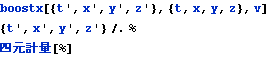
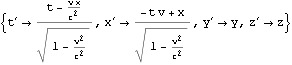
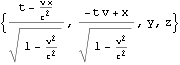
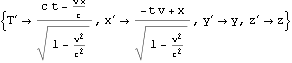
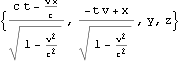
四元速度
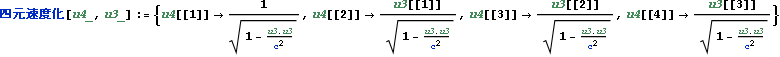
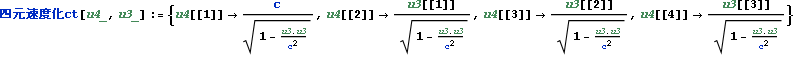
文献：パウリ上）p189によれば、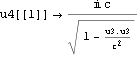
であるかのようになるが、本稿で世界点が{t,x,y,z}であることに対して文献：パウリ上）では{i c t,x,y,z}である違いによる。
文献：中野）p117 によれば、u4[[μ]]→
で文献：中野）p100のdτ=dt 
から u4[[μ]]→
→
→
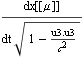となる。文献：中野）p112 では世界点が{c t,x,y,z}である。これに従えば u4[[1]]→
→
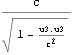である。
四元速度化の定式化,はローレンツ変換の定式化、同様、世界点を{t,x,y,z},{i c t,x,y,z},{c t,x,y,z}のいずれかとして表しているかによる。
四元速度はローレンツ変換に従う。
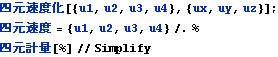
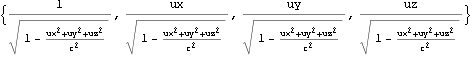
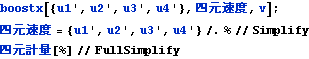
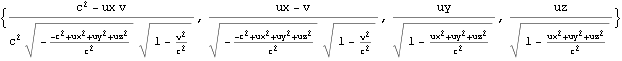
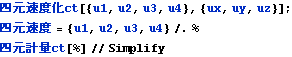
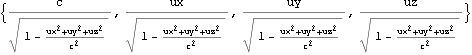
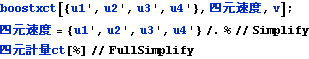
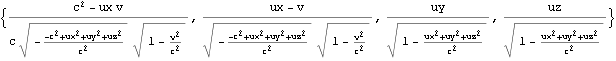
文献：パウリ上） p190にも四元速度の四元計量が
となることが示される。
文献：中野） p130 (7.7)にも四元速度の四元計量が
となることが示される。
四元速度のローレンツ変換が先の加法定理を満足することを以下に示す。速度の加法定理はK’系における三元速度{ux,uy,uz}がK系でどう観測されるかだったので、K系の四元速度がローレンツ変換でどう観測されるかと比較する（同値であるかを確認する）場合は、速度の加法定理のvの代わりに-vを使って逆変換としておく。
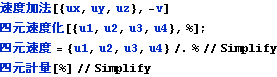
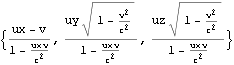
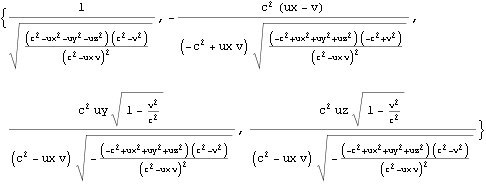
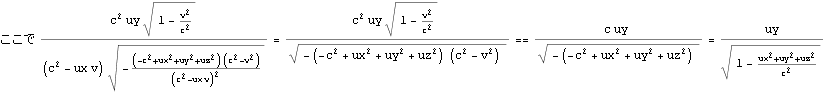
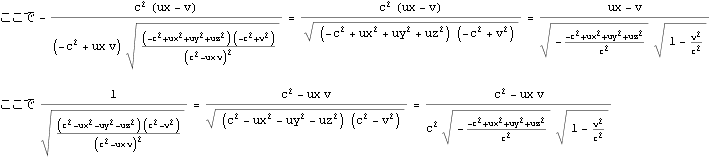
すなわち四元速度を用いれば （三元速度を四元速度に変換すれば） 速度の加法定理の公式は不用になり、ローレンツ変換だけで用が足りるようになる。
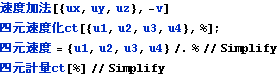
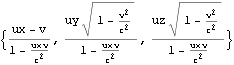
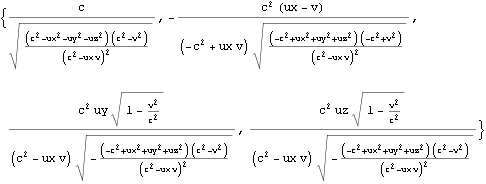
四元加速度
あらためて、三元速度は以下のように表すことができる
三元加速度は以下のようになる
世界点を {t, x, y, z} とするとき四元速度は以下となる
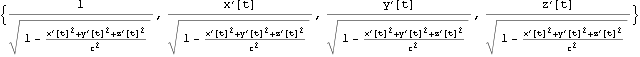
世界点を {c t, x, y, z} とするとき四元速度は以下となる
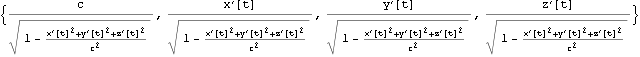
世界点を { t, x, y, z} とするとき四元加速度は以下となる
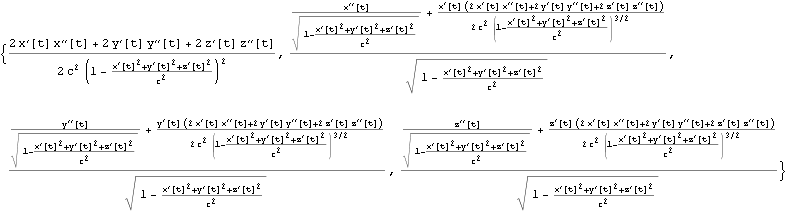
世界点を {c t, x, y, z} とするとき四元加速度は以下となる
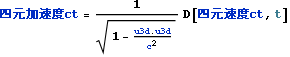
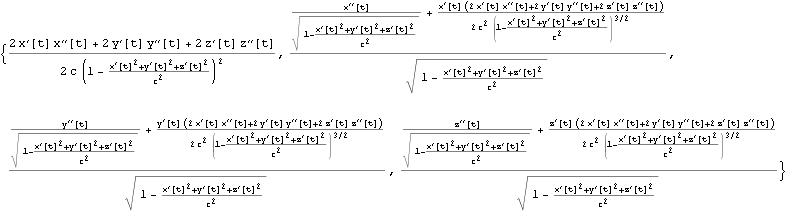
これは以下の、文献：パウリ上）p191 (193)の四元加速度ベクトルの式と同じである。
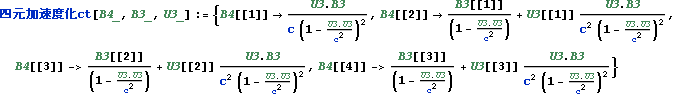
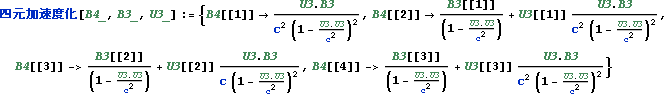
以下に、文献：パウリ上） p190 (192)の
=0 を示す。
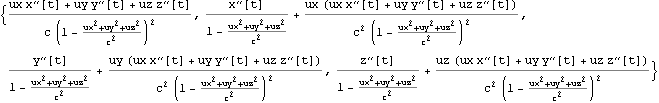
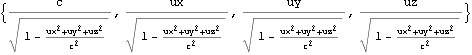
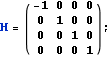
双曲線運動と 
特殊相対性理論における、質量とエネルギーの等価理論を導出することは、本稿筆者にとって難解なものである。
文献：パウリ上) p190に双曲線運動の記述がある。文献：パウリ上) では、この双曲線運動から明示的に質量とエネルギーの等価理論を導出することは成されていないが、本稿筆者のある解釈のもとで、この双曲線運動から比較的容易に質量とエネルギーの等価理論の式が現れてしまうことを示す。
以下、その解釈を示す。
ある慣性系で観測される、ある粒子に、ｘ軸に沿った運動をさせる力の場があった場合、その力を、粒子の運動距離で積分した量、すなわちポテンシャルエネルギーは、その粒子が、その運動距離で得た加速に要したエネルギーに等しい。（その力が位置によらず一定の場合は、距離と力の積が加速に要したエネルギーに等しい）
その力は、その場に静止する粒子が場から受ける力に等しい。
である。
このことは、ニュートン力学で、重力場で力、加速度、ポテンシャシャル、（水平移動が無い放物線でない）落下軌道計算等に馴染んだ者には、比較的抵抗なく受け入れられるかと思う。特に、その力は、その場に静止する粒子が場から受ける力に等しいは受け入れられるだろう。
重力場でなく電気力場である場合も同様かと思う。
しかしながら、その軌道計算は特殊相対性理論とニュートン力学では異なる。やはりニュートン力学は、運動速度が光速より十分小さい場合における近似解でしかない。後に、場の力が位置によらず一定の場合の双曲線運動について論じるが、この場合、ニュートン力学では粒子の速度は無限大に大きくなるが、相対性理論では光速度に収束することを示す。そこでは、四元加速度のローレンツ変換を利用している。
それでも、場の力を、粒子の運動距離で積分した量、すなわちポテンシャルエネルギーが、その粒子が、その運動距離で得た加速に要したエネルギーに等しいというニュートン力学と同じ法則が成立するというのが、本稿である。
ここでは、力の場を想定した。本稿筆者はこれは、力の場でなく、粒子をロケット推進する （物質ジェットの噴出の反力で推進する） 宇宙船に見たてた場合でも成立させたいと考える。
この加速する宇宙船の中で、その加速力を検知することは可能だろう。何より乗り組み員が加速度を感じるし、静止質量が既知の重りとバネ計りを使って重りに作用する加速力を計って加速度を求め、宇宙船の全静止質量から、宇宙船に作用する加速力が算出できる。
この算出された宇宙船に作用する加速力は、宇宙船の加速度運動を観測する慣性系で、その位置にその加速力の場があったと見なすことができるというのが本稿筆者の考えである。
実際、ニュートン力学でもこの考えで、すなわち、宇宙船に作用する力を加速度運動を観測する慣性系の運動距離で積分して宇宙船の加速に要した運動エネルギーを算出できる。
軌道計算は特殊相対性理論とニュートン力学では異なるというのは、ニュートン力学では、宇宙船の中で検知する加速度、すなわち宇宙船の速度を瞬時瞬時ゼロと観測する慣性系で検知する加速度と、宇宙船の加速度運動を観測する慣性系、例えば、地球からその宇宙船の運動を観測して得られる加速度は一致するが、特殊相対性理論では、そうではないということでもある。
地球などからの、粒子や宇宙船の加速度運動を観測して、その既知の静止質量から、粒子の場の加速力、それと等価な宇宙船の推進加速力を求める場合は、粒子、宇宙船が静止していると見なせる相対論的な変換をして算出する必要があるというのが、本稿筆者の解釈となる。
上記の、その力は、その場に静止する粒子が場から受ける力に等しい、という力は
実は双曲線運動の加速度に縦質量を乗じても得られる。
さらに好ましいのは、双曲線運動の横質量を用いた運動量の時間微分でも、この等しい力が得られる。
このことは、本稿筆者の双曲線運動から質量とエネルギーの等価理論を導出することの正当性の自信を深めるものであるが、双曲線運動の加速力は、場の力として、その場に静止する粒子が場から受ける力に等しいとして、それが時間によらず一定ならば双曲線運動の加速力もまた（見た目に反して）時間によらず一定という解釈が、本稿筆者の個人的な美意識にかなうまでのことである。
この解釈は文献：パウリ 上) p206 (213) において電磁的力、電子の力学でローレンツ力 
=
’ となっていることに対応する。アプリオリにこれを受け入れれば、質量増加・横質量・縦質量を介さずにこの双曲線運動から、質量とエネルギーの等価式が導出できる。
本稿筆者は、この双曲線運動を良く理解すれば、例えば力の場を成して動作する粒子加速器の設計知識にも役立つかと思う。
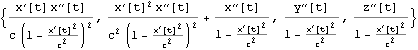
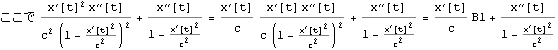
B' は上のBをｘ軸に沿った速度
でローレンツ変換しても得られるので以下となる。
ここで三元速度、三元加速度は、ローレンツ変換できなく、
四元速度、四元加速度でなければローレンツ変換はできないことに留意する
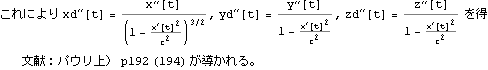
以下のように質量×速度 の運動量 を時間微分して加速力を求めると、仮定した一定加速力 
m0を得る。このとき質量は速度による増加質量を用いる。
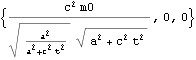
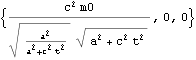
ちなみに、縦質量
は一般的に、速度による増加質量すなわち横質量を用いて、質量*速度 の運動量 を時間微分したときに表れるもので、これを以下に示す。
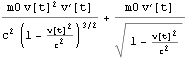
ここで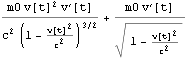
=
(
+
)=
=
=
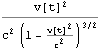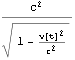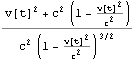
以下の手順で粒子を速度{v,0,0}までにするに必要なエネルギーを距離×力で求める
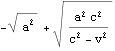
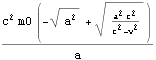
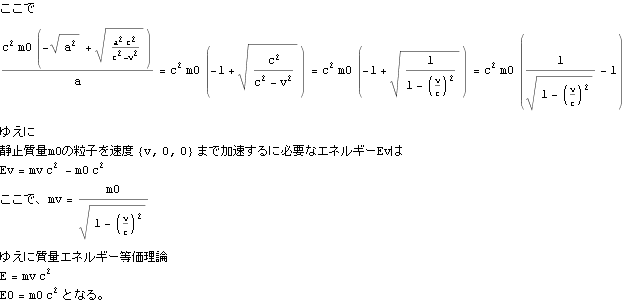
以下この双曲線運動を調べる
ここで四元加速度がローレンツ変換できることから得た、三元加速度の変換式を用いると、以下のように仮定した一定加速度
を得る。三元加速度の変換式の中に、縦質量と同型の式が紛れている。この形が横質量に負っていないことは重要だ。
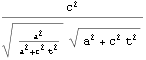
以下に、双曲線運動速度、双曲線運動加速度から、双曲線運動の四元加速度を求める
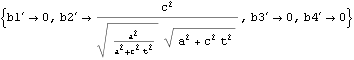
反変ベクトル と 共変ベクトル 特殊相対性理論と 行列 アインシュタインの規約
文献：パウリ 上） や 文献：中野）では、行列表記やアインシュタイン規約表記が使われる。
本稿では、質量エネルギー等価理論の導出に至るまでベクトル表記は使用したが、行列表記やアインシュタイン規約表記はあまり用いていない。
特に、本稿筆者のようにアインシュタイン規約表記になれていない者には、誤読が生じやすい。アインシュタインの時代では、こうした便利な表記規約を用いないと、紙印刷の論文ページが、内容の割りに大きくなって、使わないと不評となるかと思うが、現代、電子媒体で記す場合は書き手、読み手とも、経済的にも、その制約は小さいかと思う。
本稿筆者は、アインシュタイン規約表記を解読するのに、神経をすり減らしてしまう部類である。
本稿筆者は、幸か不幸か、Mathematicaでアインシュタイン規約表記がそのまま使えるかを知らない。
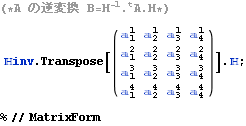
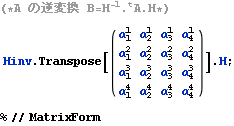
以下に、文献：パウリ 上） や 文献：中野）で行列表記やアインシュタイン規約表記で表されている内容をMathematicaで展開したので、読者の参考になれば幸いである。Mathematicaは誰にとっても、そう表記した通りにしか動作しない。
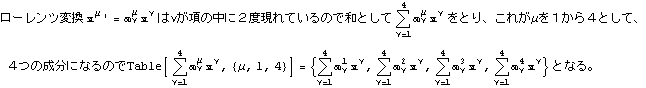
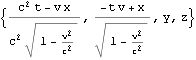
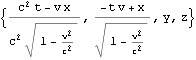
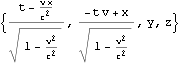
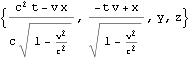
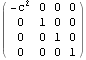
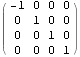
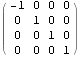
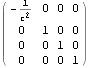
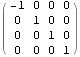
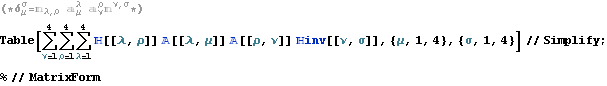
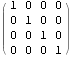
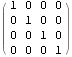
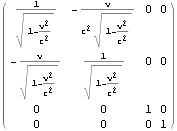
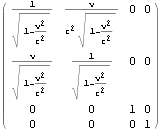
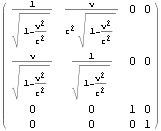
