ジャイロの質点運動方程式
Mathematicaにおける回転と外積
位置ベクトル{1,0,0}をZ軸{0,0,1}でΦだけ回転すると{Cos[Φ],Sin[Φ],0}になる。
![]()
![]()
Z軸を{0,0,2}と表現しても、結果は変わらない
![]()
![]()
Z軸を{0,0,-1}と表現すると、{Cos[Φ],-Sin[Φ],0}である。RotationMatrix[Φ ,A].Bは、右ねじの法則で回転を与える
![]()
![]()
式クリア
aaaに変数ω,θ,θ2,θ3,t,m,Φ,r2,r1が正の実数である定義を格納する。Mathematicaで式を簡略変形するときの条件となる。
式の 代入規則を蓄積するxxxを初期化する。
![]()
![]()
時刻tにおける質点の位置ベクトル
{r1 Cos[t θ+θ2],r1 Sin[t θ+θ2],r2}
は傾いていない独楽のある質点の時刻tにおける位置を表している。
この質点の回転面(旋回軌道面)は独楽の支点の地面・テーブル面からr2の距離である。
この質点の回転半径がr1、回転角速度はθ、t=0での回転角(初期位相)はθ2である。
θ2をパラメータとすることは、θ2で0\:ff5e2πで積分することにより、この質点の独楽自転による軌道上の質点の集合、すなわちリングの力学的性質を、リングの線密度と併せて、解明することができるので有利となる。
独楽の支点の座標は原点{0,0,0}で、これは以後、一貫して変わらない。
![]()
![]()
pθを質点の時刻tにおける位置ベクトルとしてpθ={r1 Cos[t θ+θ2],r1 Sin[t θ+θ2],r2}をxxxに格納した。
![]()
![]()
時刻tにおける質点の位置ベクトルの描画
式を描画する為には、数値を具体的に代入する必要がある。
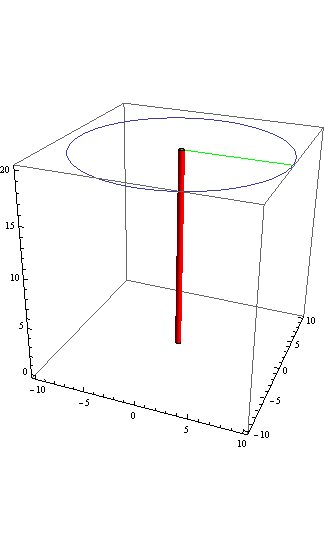
独楽の自転軸、赤い棒の長さがr2、質点の回転半径、緑の線の長さがr1である。
独楽の自転角速度を2 πとしたので、t=1 でちょうど一回転する。
Mathmaticaでこのように図解描画させると数学の意味が良く判る。図解で良く理解できるなら
数式はそれ以上である。何故なら数式はこのように図解になるからである。
ことわっておくが3次元で円を描く描画関数を使って描いているのではなく、質点の軌跡の式から描いていることが肝要である。
![]()
![]()
![]()

![]()
独楽を傾ける
この独楽の回転軸をベクトル{-1,0,0}の廻りにΦ傾けると質点の時刻tにおける位置はpθからpΦになり
pΦ={r1 Cos[t θ+θ2],r1 Cos[Φ] Sin[t θ+θ2]+r2 Sin[Φ],r2 Cos[Φ]-r1 Sin[t θ+θ2] Sin[Φ]} となる
![]()
![]()
![]()
![]()
この独楽の回転軸をベクトル{-1,0,0}の廻りにΦ傾けると質点の時刻tにおける位置はpθからpΦになり
pΦ={r1 Cos[t θ+θ2],r1 Cos[Φ] Sin[t θ+θ2]+r2 Sin[Φ],r2 Cos[Φ]-r1 Sin[t θ+θ2] Sin[Φ]} となる
描画する為には、質点独楽自転旋回中心も同様に傾ける必要がある。
![]()
![]()
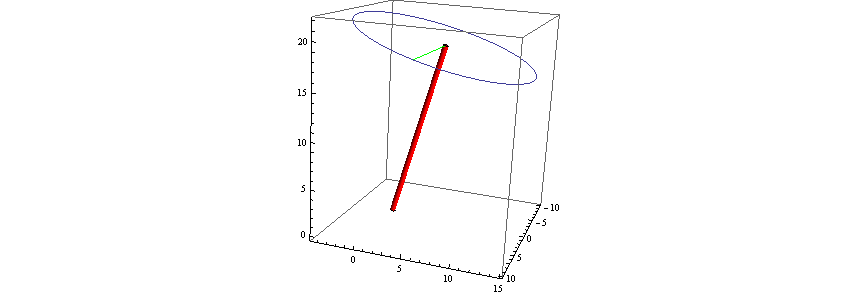
図示・描画することにより、式の正しさが確認できる。軌道は正しく傾けられている。
ことわっておくが3次元で円を描く描画関数を使って描いているのではなく、質点の軌跡の式から描いていることが肝要である。
![]()
![]()
![]()
![]()
![]()

![]()
![]()
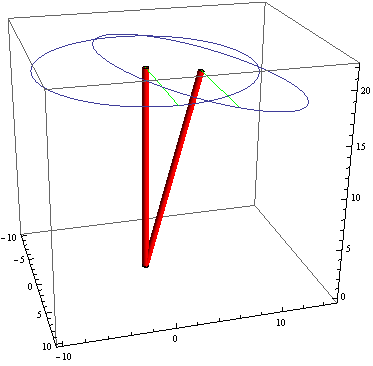
ここまでだけでは、独楽が倒れない為の力は説明できない。独楽の歳差運動、すなわちコリオリ力が導入されていないからだ。ただし、上図の質点の旋回運動における、遠心力について説明しておく。この質点が遠心力によって飛び散ってしまわないのは、実際の独楽では、独楽の材質による引っ張り応力に対する抵抗性のおかげである。内部応力とも言ったか。独楽の材質の分子間力(金属製だったら原子間力?)と言ってもよかろう。これは今後の議論でも常に遠心力と釣り合うので、この遠心力をもって、主に独楽が倒れない議論があるとすれば、それは間違っている可能性が高い。この議論はバケツに紐をつけて振り回すときの、紐の引っ張り応力の議論と同じである。紐をぶち切ろうする力・遠心力を紐の引っ張り応力が拮抗、打ち消している。
独楽の歳差運動無しには、独楽を上図のように傾けさせておくには、力がかかっている支持が必要である。もし、旋回している独楽の一部である1質点のことしか考えないのであれば、この支持には、質点の旋回周期に応じた、周期的な力が加わると思われる。なぜなら、先に述べた、質点を飛び散らせない為の独楽材質の応力(バケツの紐の引っ張り応力が)が、独楽軸に反力を与えるからである。しかし独楽は実際には回転体の形状をしているので、同一旋回軌道上にある質点どうしの力で打ち消しあって、そのような周期的な力は、支持には生じない。その意味でも、この遠心力をもって、主に独楽が倒れない議論があるとすれば、それは間違っている可能性が高い。周期的な力ではなくて、この力がかかっている支持に必要な力(重力による転倒モーメントに抗する力)を与えているのが、独楽の歳差運動による・コリオリの力、ジャイロモーメントであるというのが、この計算目的の趣旨である。
今後の議論において、この手の遠心力の存在を無視することになるのは、この様な考察に基づいている。しかし、これからの議論の独楽の歳差運動によって生じる、質点の遠心力は別である。独楽の歳差運動による・コリオリの力、ジャイロモーメントは、重力による転倒モーメントと、この独楽の歳差運動によって生じる、質点の遠心力の合計と釣り合う必要がある。いうまでもないが、歳差運動による遠心力は、重力による転倒モーメントに加えて、独楽を転倒させる方向に働く力であって、これを独楽が倒れない力とするのは真逆である。
独楽の歳差運動を表現する
傾けた独楽の質点の独楽自転運動(質点の旋回運動)に、さらに角速度ωの歳差運動を仮定してみた。
質点の時刻tにおける位置はpΦからpωになり
{r1 Cos[t θ+θ2] Cos[t ω]-(r1 Cos[Φ] Sin[t θ+θ2]+r2 Sin[Φ]) Sin[t ω],Cos[t ω] (r1 Cos[Φ] Sin[t θ+θ2]+r2 Sin[Φ])+r1 Cos[t θ+θ2] Sin[t ω],r2 Cos[Φ]-r1 Sin[t θ+θ2] Sin[Φ]}
となる。
![]()
![]()
描画に際して独楽の自転角速度θ→2 πに対して歳差運動の角速度は![]() と遅く設定した。{t,0,10}で歳差運動が1回転し、その間に独楽は10回転する。参考に傾いていない独楽の軸(赤棒)とともにこの質点の軌跡を描画した。
と遅く設定した。{t,0,10}で歳差運動が1回転し、その間に独楽は10回転する。参考に傾いていない独楽の軸(赤棒)とともにこの質点の軌跡を描画した。

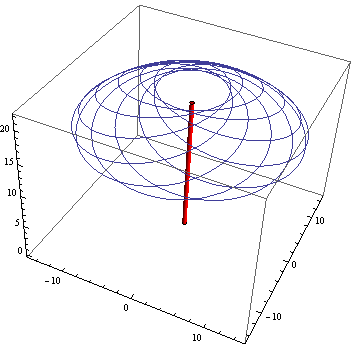
判りやすいように質点の独楽自転旋回半径をr1→3と小さくして再描画した

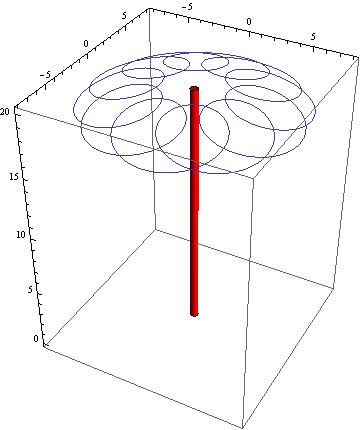
当然のことながら、この軌跡は美しいかもしれないが、やや複雑である。これを直接、愚っ直に分析して、独楽自転の遠心力、歳差運動の遠心力、コリオリの力と分析する方法もあろうかと思うが、その前に別の考え方に立ち戻りたいと思う。
コリオリの力
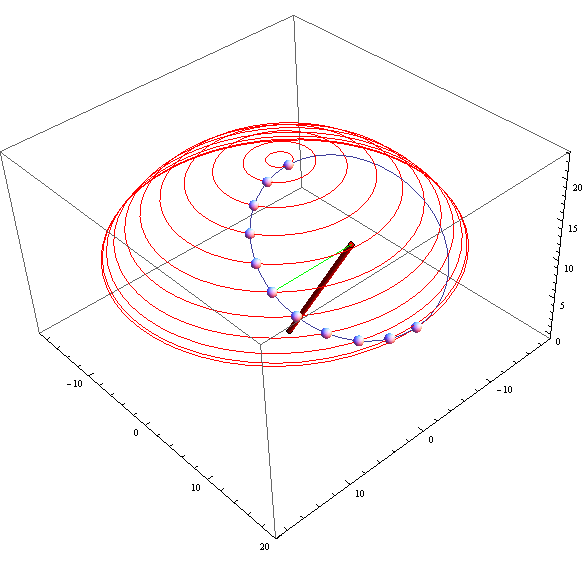
歳差運動をする独楽の一部である質点の運動は下図のように考えることもできる。下図ではこの質点の様々位置を立体的な小さな球として表現している。ただしこれは、独楽の歳差運動を止めた形で表現している。そうでなれば、質点の軌跡は先に示した比較的複雑な形になるのだが、下図の青い質点の軌跡は、3次元で傾いているとはいえ、単純な円運動である。下図において赤い曲線は、球面上にあって、地球に例えれば、等緯度線のようなものである。青い軌跡が円になっているのは、地球上に巨大な環状線があるようなものである。この環状線を見下ろす静止衛星から見れば、この巨大な環状線を走る列車は円運動をしているように見えるだろう。静止衛星はその性格上、地球の自転を観測しないからである。しかし地球が自転しているように見える宇宙船からは、列車の軌跡は先に示したような比較的複雑なものになる。自転する地球の場合、このような列車は、等緯度線を横切るとき、その等緯度線の接線方向にコリオリの力を受ける。何故なら等緯度線を横切るのは、速度の違う動く歩道を渡り乗り移るようなもので、そこに速度の変化、すなわち加速度が生じるからである。
![]()
![]()
![]()
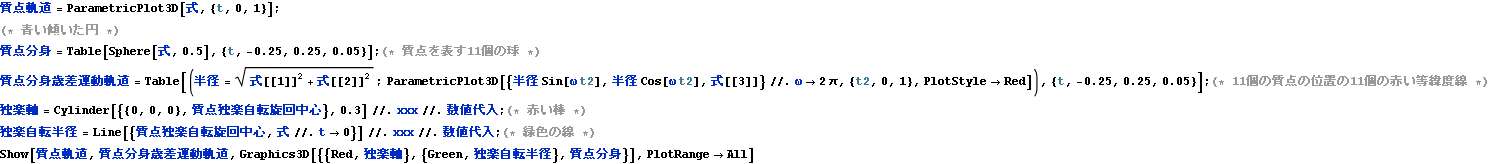
![]()
以上の見地から歳差運動(地球の自転に相当)する独楽の質点に生じるコリオリの力を調べてみよう。
pΦ={r1 Cos[t θ+θ2],r1 Cos[Φ] Sin[t θ+θ2]+r2 Sin[Φ],r2 Cos[Φ]-r1 Sin[t θ+θ2] Sin[Φ]}の
X-Y平面に投影した運動方程式(時刻tにおける位置ベクトル)をcoliRとする
![]()
![]()
pΦの位置での、歳差運動における速さcoliVを式にする。この速さは、先の等緯度線の(独楽の歳差運動による、地球の例では地球の自転による)接線方向の速さで、速さ=角速度×回転半径
を利用している。coliVはスカラー量である。
![]()
![]()
pΦの位置での、歳差運動における速さを時間で微分してコリオリ加速度coliAを求める。この加速度は時刻tで表された、傾いた円軌道の質点の位置における、先の等緯度線の接線方向のコリオリの加速度である。coliAもスカラー量である。
![]()
![]()
pΦの位置での、歳差運動における速さ、コリオリ加速度の向きのベクトルcolie(単位ベクトル)をZ軸の方向とcoliRの外積から求める
coliRは質点の位置ベクトルのX-Y平面への投影だから、歳差運動・等緯度線の半径ベクトルでもある(先の図参照)。外積をとると、この半径ベクトルとZ軸の方向に垂直になるから、等緯度線の接線方向になる。これをベクトルの長さで除すれば単位ベクトルとなる。
![]()
![]()
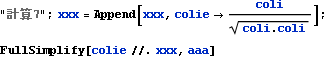
![]()
![]()
![]()
コリオリの加速度をベクトルとする
![]()
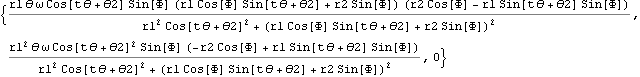
ここまでの結果を図示・描画して確認してみる。黒の矢印がコリオリの加速度のベクトルである。
このコリオリの加速度・コリオリの力が、傾いた独楽の重力、歳差運動の遠心力に拮抗・あらがい得る方向に生じていることが判る。
(コリオリの加速度のベクトルの長さを![]() にして描画している)
にして描画している)
![]()
![]()
![]()
![]()
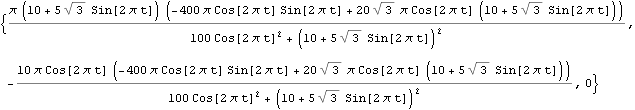

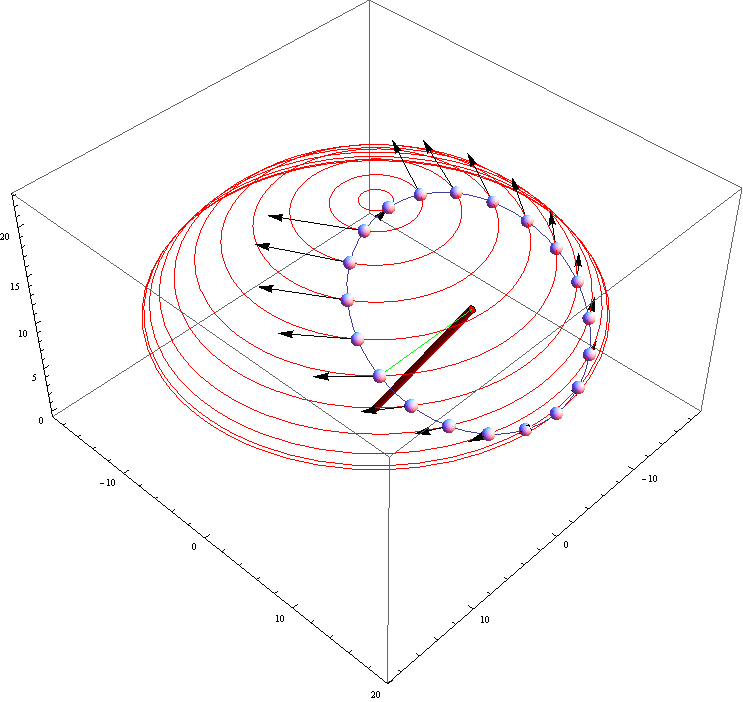
この絵が出力できたとき、正直、やった!と思ってしまった。
![]()
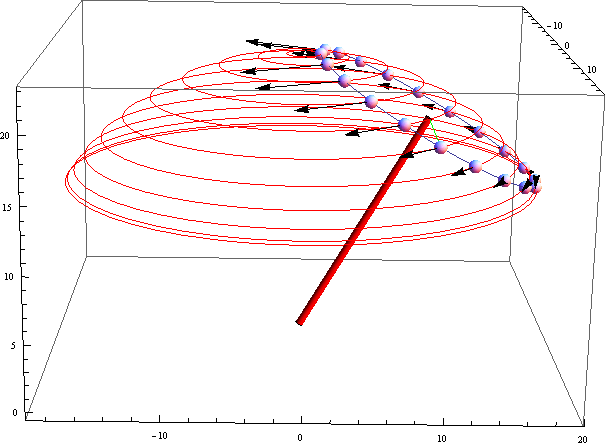
数式を用いなくても、この図から独楽が倒れない為のコリオリの力を説明できるかも知れないが、この図が描けるのは数式のお陰でもある。図で理解できるとすれば、多分にそれは錯覚でもある。数学は思考の節約でもある。物理を正しく理解しているとは、多分に物理を正しく計算できることでもある。ただ、図から例えば、この黒いベクトルの向きが間違っていないことを、言葉の論理で説明できることも物理頭ではある。この位置の質点の位置では、等緯度線接線方向の速度は増すから減じるから、コリオリの力はこの向きになるとかの判断である。その意味では数式を用いなくても定量的ではないが理解できる余地はある。式の複雑な数学的変形が苦手にしても、数学的変形が必要になる複雑な式の作り方の手順を理解できることは必要だ。Mathematicaは、簡単に描画できることと併せて、理解説明の強力なツールとなる。
次にこのコリオリの加速度・コリオリの力からジャイロモーメントを考える。
pΦの位置の、X軸からの距離ベクトルarmを考える (位置ベクトルのY-Z平面への投影)
こうしたY-Z平面への投影という場合、実は歳差運動(歳差回転)を考えると、このY-Z平面は(Z軸まわりに)回転しているのである。この辺の事情、質点の軌跡を先の青い傾いた円で考えていることを、局所座標で扱うと説明している文献・教科書が多いと思われる。
![]()
![]()
距離ベクトルarmを腕としてX軸まわりにモーメントを与える加速度の方向ベクトル(単位ベクトル)feを、X軸の方向とarmの外積として求める。feはarmとX軸に直角である。
![]()
![]()
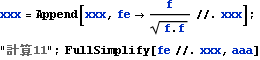
![]()
![]()
![]()
![]()
![]()
コリオリ加速度による、colieFを求める。質点の密度をmとする。colieFはY-Z平面内のベクトルである。
![]()
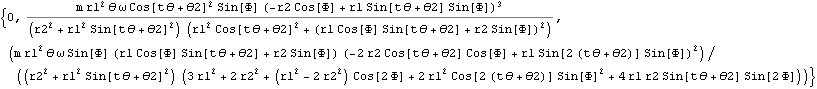
ジャイロモーメントmtを求める。モーメントは腕のベクトルarmとそれに垂直な力のベクトルcolieFの外積とするのが習慣である。(右ネジの法則)。腕のベクトルarm、力のベクトルcolieFはY-Z平面内なので,ジャイロモーメントmtはX軸方向となる。
独楽は局所座標X軸まわりに傾けたので、このジャイロモーメントmtが独楽の姿勢を保つ力となる。
![]()
![]()
![]()
![]()
上の最後の積分計算は私の環境のMathematicaで非常に時間のかかるものである。1質点によるジャイロメーメントmtは時間の関数であるが、これをθ2で0から2πまで積分すると、時間依存が解消する。これは1質点によるジャイロモーメントからリング上の独楽の一部によるジャイロモーメントを計算したことに相当し、mは質点の密度からこのリングの線密度に読み替えられる。
この結論に関してはブログの記事で触れている。http://assy0707.at.webry.info/201201/article_11.html
今回は、そのときよりもグラフィックを強化した。それも手伝って、この計算に大きな誤謬の可能性はより小さくなったとある程度、自負を深めた。
ブログで
文献1) 物理入門コース1 力学 戸田盛和 著 岩波書店 184ページ として
M g l Sin[Φ]=L ω Sin[Φ] (1)式
ここでlは 支点(独楽の芯の下端)と独楽の重心との距離)
Lは支点のまわりのコマの角運動量で
L=I θ
I はコマの慣性モーメントとされている。
と書いた。今回の私の計算では上の(1)式の右辺を検討した訳だが、私の場合は、歳差運動による遠心力は、(1)式の左辺に加えるべきものと考えていた。(1)式の右辺に歳差運動による遠心力が含まれているのか、まだ理解できていない。
今後、歳差運動による遠心力を計算してみたい。もしかしたら歳差運動による遠心力とジャイロモーメントを合わせた方が、式がより簡単になるのかも知れない。
今回歳差運動を別扱いにする、独楽が傾いただけの局所座標を用いたが、そうでない、比較的複雑な質点の軌跡を直接解析することにも再チャレンジしてみたい。