自作ソフトの補足

リバーシの思考ルーチン

リバーシの思考ルーチンについては他の人が詳しく解説しています。例えばこことか、こことか。

今回使用した方法は、

• 局面評価：パターンに基づく評価のみ
• 評価値探索：NegaScout探索法
• 高速化：候補手の並び替えと置換表（キャッシュ）を残り4手の読みまで
• その他：序盤は定石を使用

となっています。高速化に関しては最低限しか行っておらず、序盤も終盤も同じ関数で探索しているので遅いです。先読みは、最高レベルで中盤8手先、終盤18手先まで読んでいます。
定石は、人が覚えられる以上に使うのはおもしろくないと思い、一般的なものを12手までにしてあります。

盤面の表し方

高速にするためには、1マスを1バイトで表現し、縦横斜めの石を3進数で表現した数値も同時に管理する方法や、終盤は空きマスを同時に管理するなどがいいと思います。

ですが、今回は盤面を簡単に扱いたいという理由で白8x8と黒8x8を64ビット変数2つで保持しています。着手可能な手も毎回それらの変数から計算しなおしています。

着手可能な手の計算部分はJavaのソースで以下のようになっています。dataが盤面の変数でcandidateに黒と白の着手可能手が計算されます。

    private static void UpdateCandidates(long[] data, long[] candidate){
        candidate[0] = CountLines(data[0], data[1]);
        candidate[1] = CountLines(data[1], data[0]);
    }
    
    private static long CountLines(long data0, long data1){
        long mask = data1 & 0x7e7e7e7e7e7e7e7eL;
        
        long ret = CountLine(data0, data1, 8, 16);
        ret |= CountLine(data0, mask, 1, 2);
        ret |= CountLine(data0, mask, 7, 14);
        ret |= CountLine(data0, mask, 9, 18);
        
        ret &= ~(data0 | data1);
        return ret;
    }
    
    private static long CountLine(long black, long white, int off, int off2){
        long white2 = white & (white >>> off);
        long temp = white & (black >>> off);
        temp |= white & (temp >>> off);
        temp |= white2 & (temp >>> off2);
        temp |= white2 & (temp >>> off2);
        long ret = temp >>> off;
        
        white2 = white & (white << off);
        temp = white & (black << off);
        temp |= white & (temp << off);
        temp |= white2 & (temp << off2);
        temp |= white2 & (temp << off2);
        ret |= temp << off;
        return ret;
    }

パターンに基づく評価

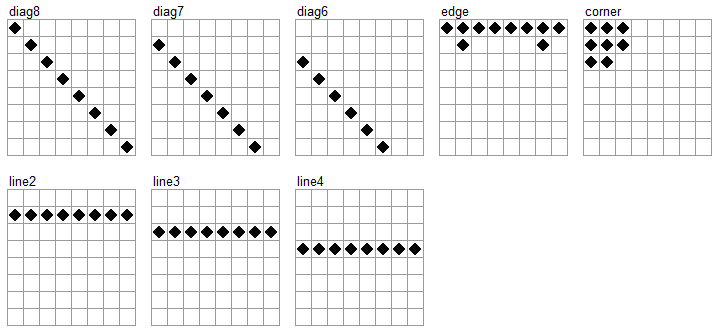
以下のパターン、黒の着手可能数、白の着手可能数、黒か白かをパラメータとして使用しています。このパターンを選んだ理由は特にありません。

パターンの係数は、以下のように求めています。

• 入力のデータ：ここにあった棋譜をそのまま使いました
  
• パターンに対する値：入手した棋譜に書いてあった最終的な石の差をそのまま結果の値としました
  
• パターンの係数の計算：対角スケーリング＋共役勾配法（CG法）
  

もう少し詳しく書くと、 i を以下のように割り当てて、

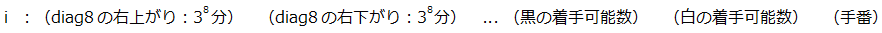
a(i)、b を以下のように定義します。

ちょっとわかりにくいですが、例えば8石で表現されるパターンは3の8乗の数値で一意に表現できるので、 i を 3 の 8 乗分割り当てます。ある局面のパターンはそのうちどこかに該当するので該当した i は a(i) = 1、それ以外はすべて a(i) = 0 とします。それを各パターンについて列挙していき、最後に着手可能数と手番を表すための i を割り当てて a(i) に着手可能数と手番の0/1を入れます。
n 個のデータが用意されているとすると、それらの a(i)、b の組は n 個あるので、最小二乗法を適用して（i は 0〜m とした）

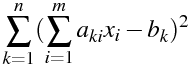
を最小にする x(i) を求めることになります。これは、最小二乗法の説明などをみると

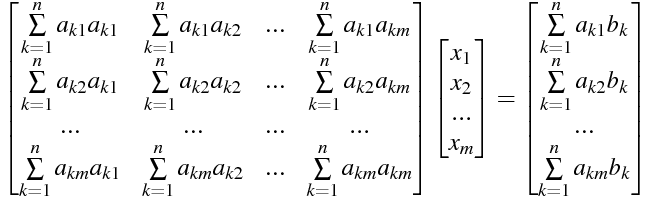
となる x(i) を求めても同じことだそうです。
これに対し、対角スケーリングを行い、共役勾配法を適用して x(i) を求めています。共役勾配法はここの擬似コードを使用しました。

ただ、単純にパターンを行列にすると大きすぎるので、以下のようにして行列を小さくしています。

• パターンに対称性があるものは逆に並べたケースと同じとみなす
  
• パターンの黒白を入れ替えたものは a(i) = -1 としてまとめた
  

計算は数分で終わりますので、パターンと石差の相関を調べて改良したり、入力データを改善したり、序盤、中盤、終盤で分けるなどの検討もできると思いますが、現在で十分な強さがあるので行っていません。

戻る