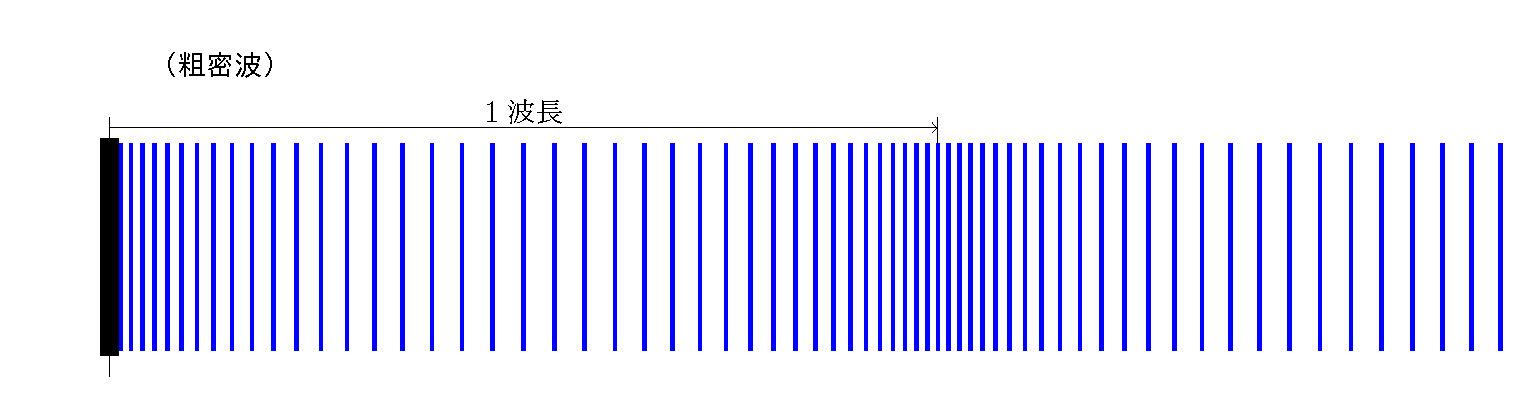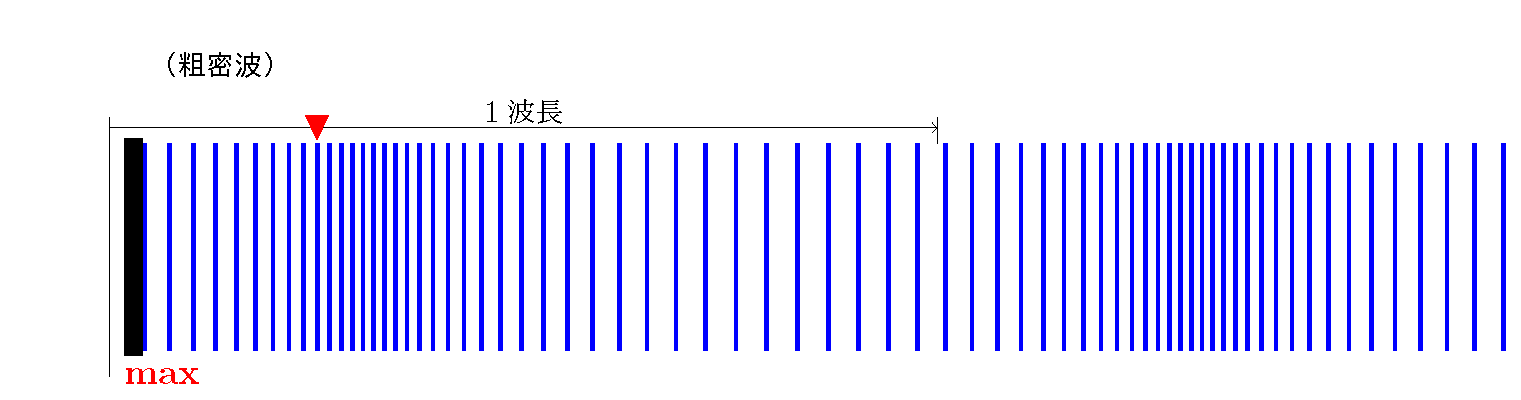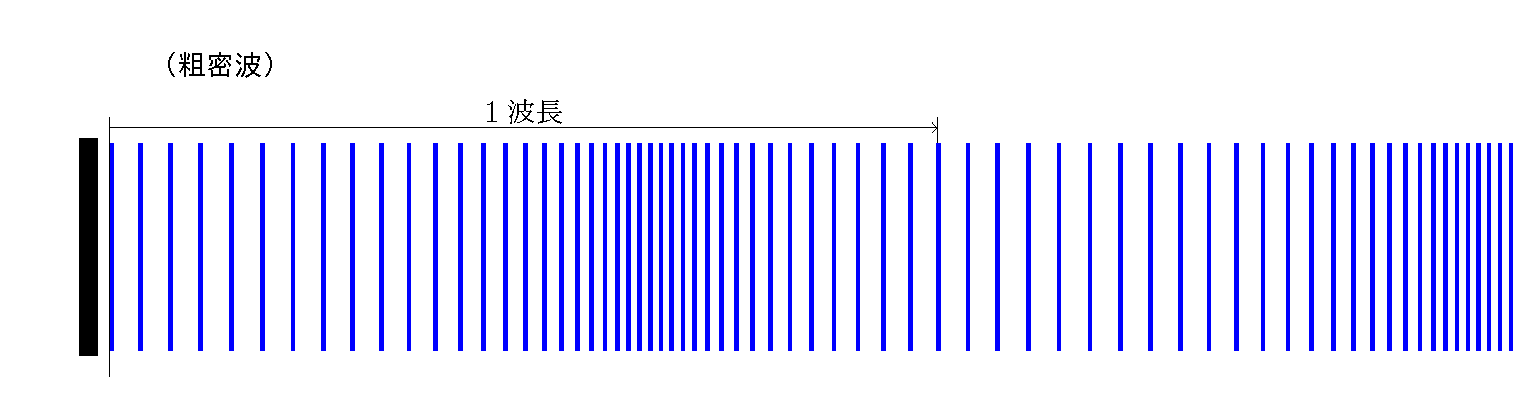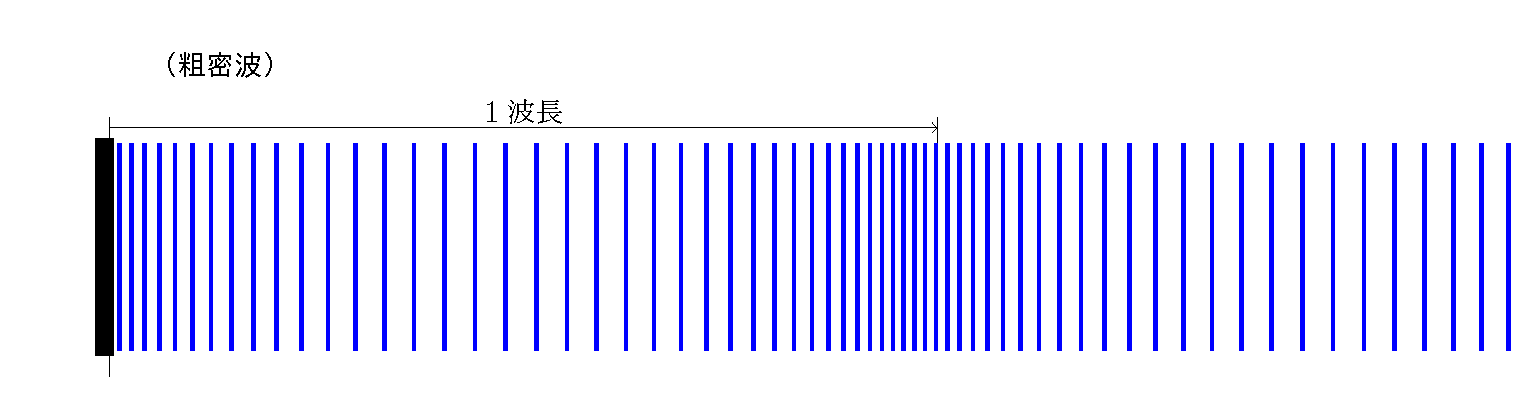
実際には音叉の腕（板）の振動の振幅は 1mm 以下，音波の波長（ 500Hz で 60cm 程度 ）にくらべて高々 1000分の1 程度である。したがって振動による腕の速さも，音速とくらべて，やはり1000分の1程度である。

　音叉の腕が，振動の中心位置を右向きに通過するときに生じた 密の部分 は，音速 で前へ伝わって行き，腕が右へ開ききる 「 1/4 周期 」後［max］には， 「 1/4 波長 」 も先［▼］へ進んでいる。 このとき瞬間的に静止する腕の前面付近では （および背面付近，すなわち音叉の内側でも）， 媒質の速度は ０，したがって 粗密変化なし（中立） である。

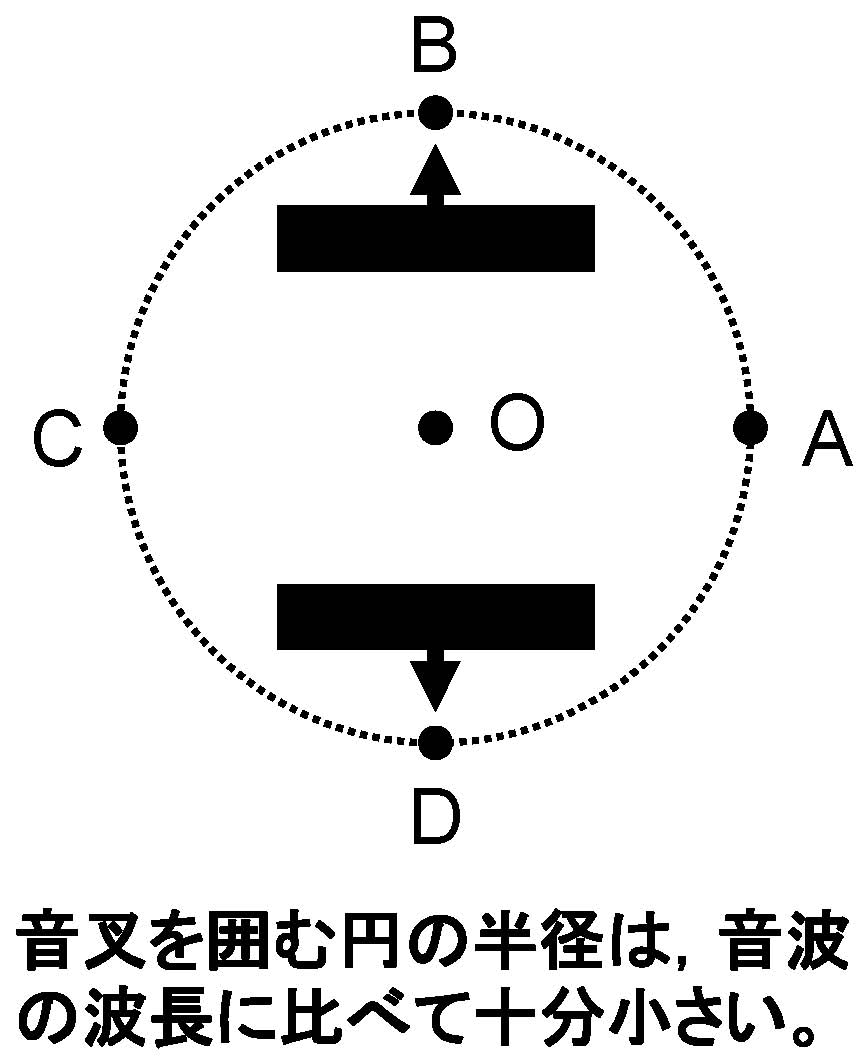　問１ では，音叉が開ききった瞬間の，『 半径が音波の波長にくらべて 十分小さい 円の周上 』 の点における疎密の状態を答えるように指示されており，物理的に意味のある結論はこれ以外にあり得ない。円の半径が波長に比べて十分小さいなら，板の表面から円までの距離はさらに小さい。

　大阪大学の回答は，要するに 「円の半径は 厳密には０でない ので，円周上の各点では正確に中立ではあり得ず，疎か密かのいずれかに決まる。粗密というのは必ずしも最大最小を意味するものではない」，すなわち図の ABCD の順に「疎密疎密」が正しいという。確かにウソではないが，この手の物理的に全く意味のない解答を要求するのは，いかにも姑息で反教育的であると言わざるを得ない。