運動の決定論性と予知不能性　　　⇒Ｗｉｎ『Ｗｏｒｄ』版


はじめに

　　「地震や噴火など原理的に予知不能なことにムダな予算をつぎ込んで」 という批判を耳にすることがある．特に数学者にこう言われるとその迫力で煙に巻かれてしまうから怖い．

　　一方，同じ意味で原理的に予知不能なはずの天気予報は，一昔前に比べれば少なくとも週間予報以内の範囲でなら格段の差で的中率が上がっていることは，少し年輩の人なら誰しも実感できよう．この 「原理的に予知不能」 とはどういうことであろうか．

　　学部の試験の答案で質問が寄せられることがあり気になっていたので，少し古くて初等的な話になるがこの機会に書かせていただこう


ケプラーからニュートンへ

　　運動の法則を現在でいう微分の概念を用いて表現したのはニュートン(1643〜1727)である．ニュートンは，物体の速度と質量をかけた量 「運動の量」（運動量） が運動にとって本質的な量であって，この運動の量を変化させる原因が力であり，「物体の運動量の時間的変化率が物体に作用している力に等しい」 ことを発見した．

　　ここで物体の運動は方向性をもつ量[1]であるから，運動量の変化というときには運動の方向の変化も含まれる．そうすると，地球の周りをまわり続けている月の運動はリンゴがまっすぐに落ちていく運動とまったく等価で，ともに地球の重力の作用であることが理解される．[2]

　　太陽の周りをまわる惑星の運動もしかり，宇宙の万物の運動はすべてこの微分の概念（微分方程式）の導入によって統一された．

　　ニュートン以前の理解は，力学の主たる対象であった惑星の運動に関する限りでは，ケプラー(1571〜1630)の法則に集大成された運動の周期と軌道に関する法則であった．

　　ケプラー自身が地動説に基づいて惑星の円軌道の半径をたがいに内接する５種類の正多面体で理解しようと試みたように，運動の理解は幾何学的であった．コペルニクス的転換を経てもなおギリシャ以来の幾何学的調和思想に支配された宇宙観へのこだわりがうかがわれる．

　　ニュートンの法則，すなわち刹那を支配する微分方程式で運動を表すということは，幾何学から解析学への発展である．ただしケプラーもすでにこの領域に踏み込んでいた．

　　ケプラーは火星の軌道が完全な円ではなく楕円であることを見ぬき，幾何学的調和の呪縛から解かれた瞬間に 『面積速度一定』 [3]という解析学的法則を見いだしており，これがニュートンによる運動の法則および万有引力の発見へと結実していった．


決定論的運動と確率論的運動

　　さて，惑星の運動が微分方程式で表されるということは，太陽を含めてたがいに万有引力（重力）を及ぼしあっている惑星系のある瞬間の力学的状態，すなわち，ある瞬間のすべての惑星の位置と速度（または運動量）がわかれば次の瞬間，その次の瞬間････と未来永劫に運動状態が完全に決定されることを意味する．

　　これを力学運動の決定論性という．惑星系の運動に限らず物体系あるいは一般に粒子系に作用している力の形が決まっている場合，事情はまったく同じである．[4]

　　決定論的運動に対して確率論的運動と呼ばれるものがある．代表的な例は元祖ブラウン運動，水の中で花粉から飛び出してフラフラと不規則に浮遊する微粒子の運動である．

　　この場合，微粒子に力を及ぼしている周りの無数の水分子[5]の運動状態を完全に知ることは現実問題として不可能であり，それ故に微粒子の運動を決定することはできない．

　　幸いにしてこの場合，夥しい数の水分子は，遅い分子，速い分子，さまざまな速さの分子の数が温度で決まるある安定した数分布を維持しており，また速度の方向に偏りはないなど，統計集団として非常に良い性質をもっている．

　　そこで水分子の力はランダムでその確率分布が決まっているとみなし，微粒子の運動を確率的に扱うことが可能になる．運動のこのような記述を先の決定論的方程式に対して確率論的運動方程式[6]という．

　　この場合には，ある瞬間の微粒子の運動状態がわかったとしても次の瞬間の運動状態を確定することはできない．その後の運動は，同じことを何度も繰り返したとした場合の期待値としてしか予測できないのである．

　　自然界の運動にはこの種の確率性を備えたものも多い．たとえば天気予報の難しさがそうである．

　　ある地域の気象を決める要素はあまりにも多く複雑であるため，我々はそのすべてを知ることが出来ないゆえに，気象の変化を確実に決定することは不可能である．この場合，できるだけ多くの要素の情報を得ることができれば予報はより確実になる．

　　実際，現在は気象衛星によって世界中の気象情報が手に入るようになり，またその膨大なデータを高速処理できるコンピュータと通信網が発達したことにより，天気予報は格段に進歩した．


予知不能性

　　さて，「原理的に予知不能」 というのはこの確率性（確定不能性）とは別で，じつは決定論的な微分方程式に従う場合であってもほとんどの運動は予知できない，すなわち，運動が 「決定される」 ことと 「予知できる」 こととは別の話だということである．

　　大学で力学を学んだ人なら必ず 「次の運動方程式の解を求めよ」 という演習問題に何度か出あっている．この場合の 「解を求める」 というのは積分形，すなわち与えられた微分方程式をみたす時間 t の（陽な）関数を見つけるということである．

　　微分方程式の解がたとえば x = A cos t, y = B sin t のように関数で与えられれば，t 秒後の状態は，初期状態から出発して次の瞬間，その次の瞬間････と，いちいち軌跡を追わなくても，積分関数に含まれている変数 t に知りたい時刻の値を代入することにより，ただちにその時刻の状態を知ることが可能[7]である．いわばこれが予知である．

　　ところが運動方程式のほとんどの場合に積分形は存在しない．つまり，出発点を決めた瞬間に行き先は決まっているにもかかわらず，それがどこであるかは実際に道をたどってみなければわからない，微小な変化量を実際に逐一積み重ねること（数値積分）によってしか行き先を知ることができない場合の方が一般的[8]なのである．


再び軌道の幾何学へ

　　このことはじつはニュートンが運動方程式を発見してすぐに知られていた．惑星系で言えば，たとえば太陽と火星，地球と月のように対象を２体に限れば解を積分形で書くことが常に可能であるが，太陽と地球と木星のように３体を扱うことになるともう一般にはこれが不可能なのである．

　　こうなると万物の運動を各刹那を支配する微分方程式で表すことによって統一したニュートンの偉大な功績も，影が薄れようというものだ．

　　実際，１９世紀末にはポアンカレ(1845〜1912)によって軌道の幾何学的性質の重要性が見なおされ，力学運動の研究は新たなレベルでケプラー的視点に回帰した．

　　そこで新たに見いだされたのは，周期的規則性をもつケプラー軌道とは質的に異なる不規則軌道 『カオス』 である．これはニュートンの微分法則にとどまる限り決して見ぬくことは不可能であった．周期軌道になるか不規則軌道になるかは，与えられた微分方程式を見ただけではわからないのである．

　「変化の規則は決まっているが，どうなるかは実際に計算してみなければわからない」，これはもうコンピュータ----今やどの研究室にも転がっているパソコンで十分----の独壇場であって，コンピュータが突出して成長した２０世紀晩期にはカオス現象がさまざまな分野において世界中で蔓延した．


カオス

　　確率論的運動方程式ではなく決定論的運動方程式（力学系）に現れる不規則運動，これがカオスである．カオスについてはもう時代遅れ，解説本も出尽くしている．ここでは一つだけ，差分方程式（離散力学系），すなわち簡単な数列の例をあげるにとどめよう．

　『 x(n+1) = 10 x(n) の小数部分 』 を発展規則とする数列を考える．この小数点から上を捨てるという操作が数学的でなく，いかにも小細工を弄しているように思われるかもしれないが，ちょっとしたグラフで表してみると何の変哲もない数列発生法である．

　　要するに小数点を下へずらしていくだけであるから，初期値を正確に与えればこの無限に続く実数列が完全に一意的に決定されることは明白だろう．

　　解析学を学んだ人なら誰でも 「実数のほとんどは無理数で，規則的な小数で表される有理数は数え（られ）るほどしかない」 ことを知っている．無理数を小数で表せば不規則な数字が無限に並ぶと信じられているから，初期値をかってに選べばほとんどの場合に 「発展規則が与えられているにもかかわらず不規則な数列」 が得られるのである．

　　実際，これに近い原理がコンピュータで乱数を発生するのに用いられており，使い道さえ気をつければ算法がいとも簡単で実用に耐えうる優れものの乱数[9]として知られている．

　　この数列の特徴は，不規則であるだけでなく次の意味で予知不能[10]であることである．初期値をいかに精密に知っていてもそれが有限である限り，たとえば小数点以下1000桁までわかっている場合，数列の第千項目から先はどうなるかわからない．

　　あるいは小数点以下1000桁まで一致する非常に近い２つの初期値のペアから出発した場合，おそらく997日目あたりまではペアはぴったり寄り添うが，そのあたりから急速に関係が怪しくなり，1000日目から先は完全に破局を迎える．予知不能のカオスには必ずこの種の軌道の不安定[11]がつきまとう．




乱

　　気象は大地を境界とし地球と共に回転する大気の流体力学現象[12]である．各地の大気の温度，圧力，流速などを扱わなければならないから，大気の運動は無限の連続自由度に対する決定論的な偏微分方程式で記述される．

　　こう言ってしまうともう何が起こっても不思議ではないと言われるかもしれないが，実際，先ほどまで整然と層をなして流れていたのに突如乱れ渦巻く乱流が発生するなど，流体の運動には仕組みがまだよくわかっていない，まさに予期せぬ現象が多い．

　　この大気の流体力学方程式を重要な変数としてわずか３変数のいとも簡単な形に縮約し，これに対する決定論的微分方程式がなおかつ予知不能なカオス解をもつことを示したのが，気象学者ローレンツ(1917〜)である．

　　気象に影響を及ぼすであろう複雑な要素のすべてを知りつくせないがゆえの確率性（確定不能性）ではなく，決定論的運動が有する予知不能性が気象変化の不規則性の本源であると考えたのである．

　　１個の粒子の運動でさえその３次元的位置と速度（運動量）で合計６変数をもつことを思えば，ローレンツの３変数モデルがいかに簡単な力学系であるかがわかろう．コンピュータでその軌跡を追ってみると，何日間か安定したほぼ周期的な運動を繰り返したかと思うと急激に別の領域に移動し，そこで再び同様の運動を繰り返す，この遷移を不規則に繰り返す････，まさに気象の転変を彷彿させる振舞いを見ることができる．

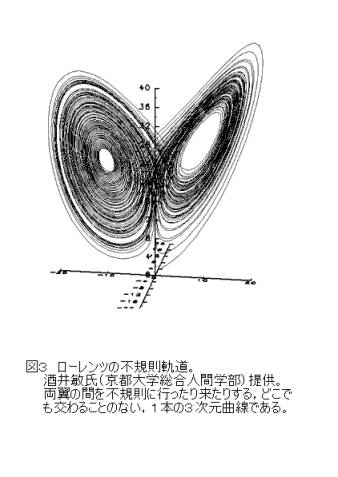→立体図アニメーション


天気予報

　　以上で，大気に限らずマントルや大陸プレートの運動などもすべて 「原理的に予知不能」 であるだろうことを理解していただけよう．しかしながら，たしかに 「なるようになってみなきゃあ先はわからぬ」 のであるが，必ずしも一寸先は闇ではない．

　　観測を重ねることによって運動の本質を的確に記述する発展方程式さえ得られたならば，スーパーコンピュータを駆使してある程度の未来を先取りして調べてみる計算機シミュレーションが可能である．

　　しかも現実問題として要求されているのは千年先，万年先の破局の予報ではない．数学的にいかに 「原理的に不能」 の誹りを受けようと，それならそれで新たなレベルの法則性を探究していくのが自然科学のしぶとさである．壮大な浪費を要することも確かだ．

　　人の一生はその人が生まれ，いや受精したとたんに遺伝子にシナリオが書き込まれるという．運命づけられているのは基本的な生命活動だけにせよ，どうか「はたしてどうなるかは実際に生きてみないとわからない」であってほしいものである．


＜プロフィール＞

冨田博之（とみたひろゆき）　1944年，兵庫県生まれ．京都大学大学院理学研究科博士課程認定退学．京都大学理学博士．現在，総合人間学部基礎科学科教授．専門は物理学で，非平衡統計物理学，パターン形成，統計幾何学などについて研究を行っている．担当科目は 『熱力学』 『計算理学基礎論』 など．主な著書に 『力学への道』 『物理学概論』 『FORTRAN77プログラミング』（以上，共著），『Fortran90プログラミング』 などがある．


＜脚注＞

[ 1]　いわゆるベクトル量．

[ 2]　月も地球に向かって落ち続けないと地球からどんどん離れてしまう．

[ 3]　惑星の楕円軌道上での運行速度は，太陽から離れているときと近づいているときで異なるが，動径が各瞬間に掃過する扇形の面積は，惑星ごとに一定値に保たれている．

[ 4]　力そのものがあらかじめわかっている必要はなく，各瞬間の物体の位置と速度だけを用いて力を表す手続きが決まっておればよい．

[ 5]　始めから水分子の存在が信じられていたのではない．この花粉の微粒子の運動が生命活動ではなく水分子の作用であると見ぬいたのがブラウン(1773〜1858)で，歴史的には分子の実在を証拠づける現象の一つとなった．

[ 6]　ここでは話をわかりやすくするため両者をあたかも対立する概念であるかのように扱っている．しかしながら，本来決定論的力学にしたがっているはずの分子運動に現れる確率性，しかも非常に良い統計集団をなすことの保証，じつはこのこと自体が歴史的には後で述べるカオスに至る探究の入り口の一つであった．（エルゴード問題）

[ 7]　積分の表式を実際に見つけることが出来なくても，古代より人類がそうしてきたように，運動が周期的であれば経験的に予知可能である．

[ 8]　「にもかかわらず大学の力学の講義では微分方程式の解を求めることに時間を費やしすぎている」 という批判もある．

[ 9]　同じ初期値から出発すれば完全に同じ数列しか得られないという意味で，真の乱数列とは異なる．これは計算機実験などに利用するときには再現性があるという意味でかえってつごうがよい．

[10]　この例は一般項の形を式で書くことが可能で，先の積分不能性とは少し事情が異なる．

[11]　これは，さすがのコンピュータもお手上げであることを意味している．数値を符号化して扱う現在のディジタルコンピュータは有限精度という宿命を負っている．

[12]　液体や気体は無数の分子から構成されるが，これを自由に変形する連続体とみなすとき流体という．個々の分子にとらわれるよりこのような見方をする方が，液体や気体の運動を的確に表現することができる．
もどる