太陽の光を巨大なレンズで一点に集めれば、他に何の変化も残すことなく、太陽の温度よりいくらでも高い温度が得られるじゃない？


　　誰でも小学生の頃、一度は遊んだことがあるだろうし、４年に一回、オリンピックの聖火の点火に使われている原理。そもそも遠方の太陽の像が生じる点が「焦点」なんて、実直そのもの。この原理を用いたソーラークッカーという調理器もあり、大がかりな装置は太陽炉と呼ばれている。

　　さて、クラウジウスの答えはノーである。どんなに焦点距離の短いレンズを使おうと焦点の半径をゼロにはできず、焦点は有限の大きさを持つからだ。有限の大きさの焦点に物体を置けば、これもまた熱放射体となるのである。

　　絶対温度 T の物体の表面から放射されるエネルギー流を単位面積・単位時間あたり F(T) としよう。シュテファン-ボルツマン則は F(T)=σT⁴ であるが、ここでは F(T) は T の増加関数でさえあればよい。

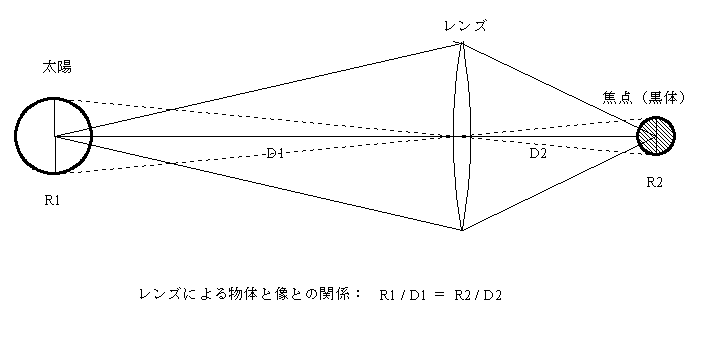
　　太陽の半径を R₁、表面温度を T₁、太陽とレンズの距離を D₁、レンズと焦点の距離を D₂、焦点の半径を R₂、レンズの面積を A としよう。焦点にこれと同じ大きさの黒体を置いたとして、黒体の温度が T₂になったとしよう。レンズを通って太陽から黒体に供給される放射エネルギーは、単位時間あたり

　　　　　4πR₁² F(T₁)×(A/4πD₁²) = A(R₁/D₁)² F(T₁)　　　　　(1)

である。一方、黒体は受け取ったエネルギーを周りの空間に熱放射することにより冷却されるが、ちょうど(1)と等量のエネルギーを放出するときエネルギー収支が釣り合い、熱平衡に達しているのである。すなわち

　　　　　4πR₂² F(T₂) = A(R₁/D₁)² F(T₁)

したがって

　　　　　F(T₂)/F(T₁) = A(R₁/D₁)²/4πR₂²　　　　　(2)



ここで、レンズの幾何光学の公式

　　　　　R₁/D₁ = R₂/D₂

を思い出せば、(2)は

　　　　　F(T₂)/F(T₁) = A/4πD₂²　　　　　　　　　　(3)

となる。図から明かなように、レンズの面積 A は半径 D₂ の球面の面積の一部分である ［正確には立体角の関係］ から、以下の不等式が得られる：

　　　　　F(T₂)≦F(T₁)　したがって　T₂ ≦ T₁　　　　　　　　　　　　(4)

　　黒体の温度を高くするには、黒体を反射壁で取り囲んで受け取った放射エネルギーをできるだけ逃がさないようにすればよいのであるが、最低限、レンズを通ってやってくる光を通す分だけは窓を開けておかなければならず、逆にこの窓から光が逃げ出す ［レンズを通って太陽に返される］ ことだけはどうしても避けられないのだ。これが等号の成り立つ場合である。

　　それじゃあ、この窓に紫外線や可視光はよく通るが赤外・遠赤外線は通りにくいガラスをはめておけば、「温室効果」で T₁ より高くできるじゃないか？なんて言わないでよね。