モンティ・ホール問題とベイズ統計
　　この問題を初めて聞いたのは 1 年ほど前、確かビートたけしが司会するバラエティ番組だった。

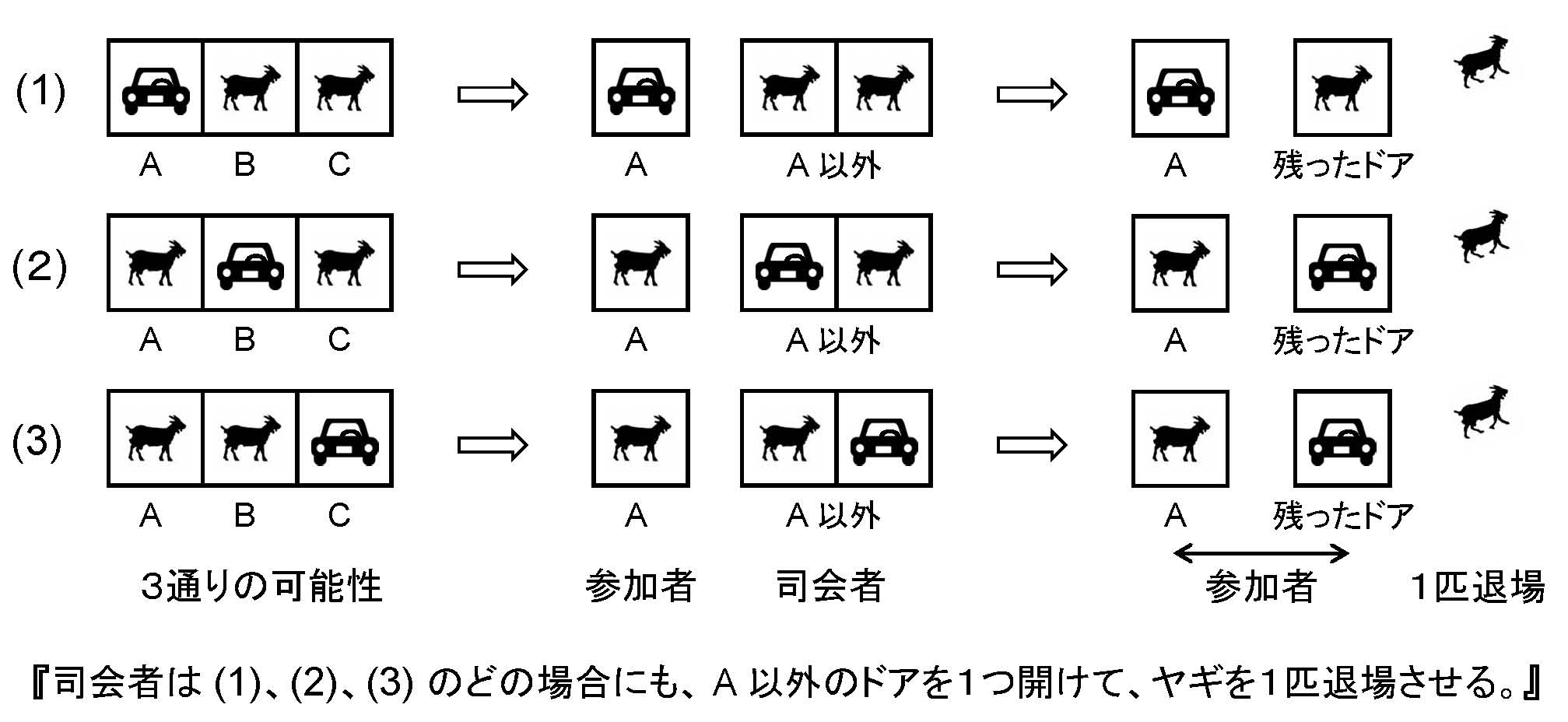
　　Ａ、Ｂ、Ｃの3つのドアのうしろに、1箇所だけ 新車 が、あとは ヤギ が隠されている。司会者は先ず参加者に 「どれか一つのドアを選んでください」 と言う。

　　参加者が選んだドアの前に立った後、司会者は 「次は私が選びます」 と言っておもむろに別のドアを開けて、中から出てくる ヤギ を見せ、「さあ、車 はあなたの選んだドアの中か、残った１つのドアの中か、どちらかということになりました。どちらを選ぶか、変えてもいいですよ。１回だけ1分間のチャンスをさしあげます。さあ、どうしますか？」 と煽り立てる。

　　参加者は 「残りのドアは２つだから、車 が当たるか当たらないかの確率はどっちみち半々。それなら最初の勘を信じよう。」 と考えて、選んだドアを変更しない。（あるいは変更しても同じことだし．．．）

　　私はテレビのこういうクイズ番組は横になりながら気楽に構え、あまり深く考えないで即座に答えを出してしまう方だから、一瞬の直感でこの参加者と同じ結論に至ってしまった。しかしながら生来、あるいは職業柄か、多少は ヘソ曲がり なところもあるので、次の瞬間には 「こんな簡単なことがわざわざ番組で取り上げられることはおかしい。ましてやビートたけしだ、何かウラがあるに違いない」 と反省、しばし画面を離れて第２の結論に至る ：

　　「最初に選んだドアが ハズレ だった場合は、変えたら必ず車が当たる。」
　　「当たり だった場合は、変えない方がいい。」
　　「最初に選んだドアがハズレだった確率は 2/3、当たりだった確率は 1/3 」
　　-----　なんと、ドアを変える方が、車が当たる確率は２倍も高いではないか！

ものの数十秒もあれば中学生でもたどり着ける、いたって安直な結論であり、最初の直感と大差はない。あとで 「大論争になった」 と知り、自問自答して苦悶することになる。

　　番組にもどってみると、案の定ウラがあり、たけしが 「この誰でもすぐに思いつく（最初の）結論に対して、ある有名な女性数学者が 『変えた方が当たる確率が2倍高い』 と異論を唱えたことから、アメリカの数学界で一騒動おきた」 と、得意そうに披露していたのである。中には 「この女はどこの大学で、どの教授から確率を習ったんだ！」 というジェンダーハラスメントまがいの誹謗さえ一流の数学者から寄せられたという。

　　私の安直な第二の結論は偶然にも彼女の結論と一致したのであるが、なんと「大論争」 の末、彼女が正しいということになったというのだ。ご丁寧にコンピュータ・シミュレーションまでやって確かめた人もあるという。まあ、バラエティ番組のことだから、多少はおもしろおかしくする誇張はあるだろうが、たしかに 「モンティ・ホール」 で検索すれば、ネット上に 「有名な問題」 としてたくさんの解説が掲載されている。確率の問題では、もっともらしい一瞬の直感が誤りを冒すことが往々にしてあるという好例に違いないが、どの解説もいささか込み入っていて、中学生ならギブアップしてしまいそうなものばかりである。

　　　「易しい」 というのでも、車がどこに入っているか、参加者がどのドアを選ぶか、司会者が残りのどちらを開けるかの、全部で18通りの組み合わせを列挙して図示し、ドアを変える方が得になるか、損になるかを判定し数え上げて説得にかかる。自分でもやってみたが、これがなかなかうまく結論に達しない。逆に難しいのは 「ベイズ統計の有名な応用問題」 を標榜するいささか専門的な扱いで、これなら 「数学界で大論争になった」 というのも頷ける。

　　ベイズ統計は、「ある原因のもとで、ある結果が起きる確率」 という通常のありふれた推定と違って、

　　　　　「結果を知ってから、いくつかある原因のどれが確からしいかを確率的に推定する」

というもので、最近、いろんな分野で使われるようになってきた。犯罪捜査や、情報処理におけるエラーの原因の推定、マルウェアの判断などにも利用されているという。　ベイズ統計は、条件付き確率に関する 「ベイズの定理」 を応用した以下の公式を基本としている：

［ 記号：　「 a である」確率を P(a)、「 b のときに a である」 条件付き確率を P(a | b) のように表す。 ］

　　------ 幾つかの（互いに独立な）原因 C₁ , C₂ , C₃ , ．．． があって、結果 R が起きたとし、

　　　(1) 『それぞれの原因 C_i が起きる確率 P(C_i) 』

　　　(2) 『原因が C_i のときに結果 R がもたらされる （通常の）条件付き確率 P(R | C_i) 』

はわかっているとする。

　　　　　『結果 R が起きた場合に、原因が C_i であった （事後）条件付き確率 P(C_i | R) 』

は、結果の事象 R を原因別 に仕分けて、原因が C_i である比率

　　　　　P(R かつ C_i) / ［ P(R かつ C₁) + P(R かつ C₂) + P(R かつ C₃) + ．．． ］

を求めればよいだけである。 分母は、事象 R が起きるすべての可能性を尽くしているから、あわせて事象 R が起きる確率 P(R) そのものであるが、これは事前には分かっていない。分かっている場合は、それを使えばよい。　ここで条件付き確率の定義式

　　　　　P(b | a) = P(a かつ b) / P(a) , 　P(a | b) = P(a かつ b) / P(b)

から導かれる等式（「ベイズの定理」）

　　　(3) 　P(a | b) P(b) = P(b | a) P(a) = P(a かつ b) ,　あるいは　P(a | b) = P(b | a) P(a) / P(b)

を用いて書き換えれば、事後条件付き確率を、すでに分かっている通常の確率 (1) (2) だけを用いて表すベイズ推計の基本公式

　　　　　P(C_i | R) = P(R | C_i) P(C_i) / P(R)

　　　　　P(R) = P(R | C₁) P(C₁) + P(R | C₂) P(C₂) + P(R | C₃) P(C₃) + ．．．

が得られる。 少しでも確率の数式に慣れた人なら、この公式は何のことはない、（現在ではほとんど自明に近い　※ 1 ） ベイズの定理 (3) を繰り返し用いて書き換えたにすぎないと思っておけば、気楽につきあうことができる。［ ※ 1． ベイズはニュートンより少しあとの、18世紀のイギリスの数学者 （牧師）。実際、私は最近手にした本を見るまで、この等式が 「ベイズの定理」 と呼ばれていることを知らなかった。 ］ ------


　　今の問題なら、例えば 「参加者は最初にドア Ａ を選び、司会者はドア Ｂ を開けた」 としよう。ほかの組み合わせの場合でも、あとの事情は変わらないから、この場合だけに限定して考察すればよい。　このとき、司会者が 「ドア Ｂ を選ぶ」 という結果（＝条件）のもとで、 原因である 「もともと Ａ に車が入っていた」 「もともと Ｃ に車が入っていた」 確率を推定すれば、変えた方が損か得かを判定できるわけである。

　　「車がドア Ａ にあった」 を 「車Ａ」 のように、「ドア Ｂ を開ける」 を 「開Ｂ」 のように書くとして、まず

　　　　　P(車Ａ) = P(車Ｂ) = P(車Ｃ) = 1/3

は明らかというか、公平なゲームの前提条件である。 次に、司会者は必ずヤギのドアを開けるのであるから、

　　　　　「車Ａ」 のときは、司会者はドア Ｂ 、Ｃ のどちらを開けてもよいから、P(開Ｂ | 車Ａ) = 1/2

　　　　　「車Ｂ」 のときは、Ｂ を開けることはないから、P(開Ｂ | 車Ｂ) = 0

　　　　　「車Ｃ」 のときは、Ｂ を開けるしかない から、P(開Ｂ | 車Ｃ) = 1

したがって、(3)により

　　　　　P(車Ａ | 開Ｂ) P(開Ｂ) = P(開Ｂ | 車Ａ) P(車Ａ) = (1/2)×(1/3) = 1/6

左辺の P(開Ｂ) は、参加者が Ａ を選んだ場合、残りの Ｂ と Ｃ は対等であり、司会者が Ｂ、Ｃ のどちらを開けるかは同等に予期されるから

　　　　　P(開Ｂ) = P(開Ｃ) = 1/2

である。実際、

　　　　　P(開Ｂ) = P(開Ｂ | 車Ａ) P(車Ａ) + P(開Ｂ | 車Ｂ) P(車Ｂ) + P(開Ｂ | 車Ｃ) P(車Ｃ) = (1/2 + 0 + 1)×(1/3) = 1/2

となっている。 以上より、欲しかった事後条件付き確率は

　　　　　P(車Ａ | 開Ｂ) = P(開Ｂ | 車Ａ) P(車Ａ) / P(開Ｂ) = (1/6) / (1/2) = 1/3

同様にして

　　　　　P(車Ｃ | 開Ｂ) = P(開Ｂ | 車Ｃ) P(車Ｃ) / P(開Ｂ) = (1/3) / (1/2) = 2/3

よって、司会者がドア Ｂ を開けた場合には、参加者は Ａ から Ｃ に変える方が車が当たる確率は２倍高くなる　．．．．

というわけであるが、ドアを前にしてこんな調子で悠長に思案していたら、時間切れで失格になってしまうに違いない。


　　この例のように、原因 C₁ , C₂ , C₃ , ．．． の起きる確率が 平等 である場合には、ベイズの公式はずっと簡単になり、

　　　　　　P(C_i | R) = P(R | C_i) / 分母，　分母 = P(R | C₁) + P(R | C₂) + P(R | C₃) + 　．．．

と書くことができる。ここまで来ると、きわめて納得しやすく、覚えておきやすい様子になっている ：

　　　　　「結果が R であったときの最も確からしい原因は、結果 R をもたらす（条件付き）確率が最も高い原因である。」

今の場合なら、上で求めたように 「車Ａ」 または 「車Ｃ」 だったときに司会者がドア Ｂ を開ける条件付き確率は、それぞれ P(開Ｂ | 車Ａ) = 1/2、および P(開Ｂ | 車Ｃ) = 1 だから、ただちに 「司会者がドア Ｂ を開けた場合、車が Ｃ に入っていた確率 P(車Ｃ | 開Ｂ) の方が P(車Ａ | 開Ｂ) より高い」 ということになる。こういうベイズ統計の妙を知っておれば、迷うことなくドアを変えることができたわけだ。やはり金持ちになるには統計学に通じておくに如くはない。


　　最初に誰しも陥る錯覚のどこが誤りなのだろうか？ ---- ドアの中身を知らない参加者と対等な立場であるかのように振る舞った、司会者の巧みな演技に目をくらまされたのだ。その場合なら、確かに司会者がドア Ｂ を開けて 「ヤギだとわかった」 瞬間にご破算となり、三択から二択に転じる。司会者でなくて、別の参加者が Ｂ を開けてヤギであった場合と同じことである。しかしこれではゲームは何の変哲もない、ありきたりのものになってしまう。

　　他でもない、すべてのドアの中を知っている司会者が 「ドア Ｂ を選んだ」 ことに、何らかの作為があることを嗅ぎつけなければならなかったのだ。要するに司会者は 「手元に当たりがあれば必ずそれを残す」 という小細工をやっている。そのことを逐一、確率という数値で説明してくれるのが上のベイズ統計の計算である。これは中学生には少し難しいかもしれない。

　　この場合、参加者の選択を見た司会者が、残りの２つのドアの 「いずれかを選んで開けた」 ことが 「結果」 であって、その中が 「ヤギだった」 ことではない。ここがこの問題の重要なキーポイントである。司会者は中身を知っているから、必ずヤギのドアを開けるのだ。（そうでなければ、単に 「イチかバチか」 のゲームで、何ら頭を使うことはない。） この程度の推論なら、わざわざ馴染みのないベイズ統計を持ち出すこともないのであるが、この「原因」 と 「結果」という事象の関係を正確に把握する上で、ベイズ統計の考え方が役に立っているのだ。


　　私の（第二の）安直な計算では、残念ながらこのあたりの事情がすっきりと見えてこない。 ----- 鋭い中学生に 「ドア Ｃ に変えた方がいいと言っても、Ｃ だって Ａ と全く同じで、当たり 1/3、はずれ 2/3 だったではないですか？ Ａ の確率は元のままと考えて 『ドアを変えた方がいい』 と結論を出したくせに、どうして Ｃ の確率が当たり 2/3 に変わったことには平気でいられるんですか？」 「ドア Ｂ の中がヤギだったことに変わりはないのに、司会者が開けた場合と他の参加者が開けた場合で、どうして Ａ の当たりの確率が違ってくるんですか？」 と矢継ぎ早に質問が飛んでくる　．．．

　　「中身を知っている司会者は、残りの二つから確実にヤギだと分かっているドアを開けることにより、ゲームの場からヤギを１匹 退場 させる。それがこのゲームのルール です　．．．」 と、 上から目線の 苦し紛れの言い訳を続けなければならない。普通の中学生なら再び煙（けむ）にまかれ、鋭い中学生は再び目を光らせて穴を探すことだろう。

　　----- 「司会者がヤギの入っているドア Ｂ を開けた瞬間に、(2) のケースは除外されたじゃないですか？」 ----- 「司会者のやることに一々目を光らせないで、ゲームのルールだけを考えればいいのです。司会者が Ｂ を開けたとしたのは、上のように原因の確率を計算してみるためです。Ｃ を選んだ場合についても計算してみてください。全く同じになるはずですね。つまり、Ｂ を選んだか、Ｃ を選んだかということは、気にしなくてもよかったということです。ヤギが１匹、ゲーム会場から去っていくところだけ、しっかり見ておればよいのです」

　　「 しかしぃ、何だかなぁ？ ．．．　でもぉ、僕が目をつぶっている間に司会者がやったか別の参加者がやったか知れないけれど、ともかく残りのドアが２つになっていて、ヤギが１匹去っていくのが見えたら、やっぱり当たりはずれは半々と思ってしまいます。」 ----- 「今度は 『Ｂを選んで開けたらヤギだった』 ことを 『結果』 とみなして先ほどと同じ計算をやれば、ちゃんと直感通りに半々になります。ブラックボックスの中で起きたことは同じだのに、『誰が開けたか』 によってＡのドアの確率が変わってくるというのは、おもしろいよね。」

　　----- 「それ、それですっ！始めに聞きたかったのは」 ----- 「１回の事例（サンプル）、例えば１回ゲームをやって 『ヤギが１匹、出て行く』 ことを見ただけで結論を出すことはできないというのが、確率現象です。２個のサイコロが振られて１の 『ぞろ目』 が出たからといって、『イカサマだ！』 と騒いだりしたら、間違いなく袋だたきにあい、裸にされて川に放り込まれるよね。今の場合も、何回も繰り返してみたら（それを想像してみたら）、司会者が開ける場合と他の参加者が開ける場合との違いが見えてくるんではないかな？」

　　「．．．．．ん’となく、なっとくです。それじゃあ、元の 3 通りの可能性がすべて等しく確率 1/3 であることは、インチキなしにちゃんと保証されているんですか？」 ----- 「 それなんだよね、肝腎なのは。まあ、参加者は最初に 3 つのドアから 好きな所を選ぶことができるわけだし、車が１台、どこかに入ってさえおればいいんじゃない？」

　　（だめ押し）　少し極端にして、仮にドアが 100 あり、車はやはり 1 箇所だけとして考えたら、よく分かるという。司会者が次々にヤギのドアを開けていって、参加者が最初に選んだドアとあわせて残りが 2 つだけ になったとき、確かに 「一方は車、もう一方はヤギ」 である。やはり 「当たりはずれは半々の確率」 と思うか？ というわけだ。私なら真っ先に 「もし司会者側に車が入っているとしたら、98 箇所もドアを開けていけば、確率 98/99 で車が出たはずだから、これはあり得ないこと。ぜったいに変えない方がいい！」 と、またも錯覚を起こしてしまう（ ※ 2 ）。 ところが、上と同じような絵を頭の中で描いてみれば、ちゃんと逆らしいと思えてくるから不思議だ。

　　司会者が次々にヤギのドアを開けていくと、「どのドアを開けたか」 なんて気にしておれなくなってしまう。司会者がいくらドタバタと動き回ろうと、参加者のドアの当たりの確率が 1/100 という事実は動かないから、それ以外の 99 箇所のドアに 1/100 ずつ散らばっていた当たりの確率、あわせて 99/100 が、ヤギのドアだけ開けていくという司会者の恣意的な作業によって最後のドアに寄せ集められていくのである。 ----- 要するに司会者は、「あなたが最初に選んだドアか、残りの 99 個のドア群か、どちらを選んでもいいですよ」 と言っているのだ。 「え？そんなにヤギはいらないって？ああ、ご心配なく。こちらのヤギは追い出しておきました。でも、１匹だけは覚悟しておいてくださいね。」

　　［ ※ 2 そのくせ 「自分が当たっている確率もわずか 1/100 」 ということには考えが及んでいない。この確率的な異様さに気がつけば、「司会者が何か仕組んでいるに違いない」という疑いが濃厚になる。］

もどる