4D-Talk

まったいら

４次元空間において、３次元図形は平らな図形になります。
で、平らな図形って、なんでしょう？
３次元において平らな図形は一目瞭然です。
特定の方向にまったく厚み（長さ）を持たない図形のことです。
４次元においても同様で、特定の方向に長さを持たない図形が平らな図形ということになります。
例えばＸＹＺ方向にそれぞれ１の長さを持つ立方体は、Ｈ軸方向に長さを持たないため、
平らな図形、ということになります、が、なかなか平らなイメージが湧かないと思います。

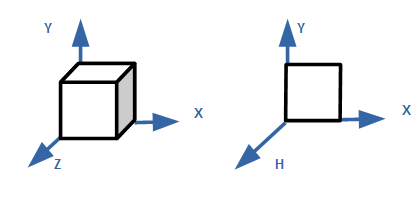
逆に、平らな図形から４次元方向に図形を構築してみましょう。
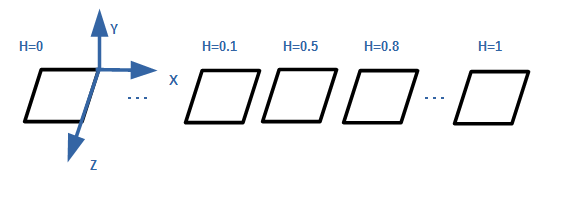
まず、正方形（２次元図形）を思い浮かべます。これは当然平らな図形です。
これをＨ軸方向に移動させて行きます。正方形の１辺の長さ分移動させるまで、
各３次元空間にこの正方形（と同じ形）が表示され、長さを上回った時、
表示される図形は無くなります。

こうしてできた図形は（感覚的につかみにくいかもしれませんが）立方体（３次元）となります。

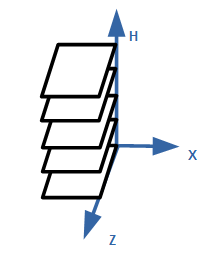
しかし、Ｈ軸の各地点において表示されているのは確かに平らな図形である正方形です。
そうして、Ｈ軸方向が今見ている平らな方向とは異なる方向であることを思い出して、
今見ている平らな方向に平らなのだと納得するのです。