円や球などが接するような問題を解くためによく使われる方法として、反転法という「半径の逆数を使う方法」があります。 

和算にはこの方法がなくて、ピタゴラスの定理のような比較的基本的な方法で得られた解答が多いので、その解法は長くなりました。 

しかし、反転法を利用すると、その解法は極端に短くなります。

反転法は、任意の点を，その点から原点までの距離の逆数に比例する距離に移す，という写像変換の一手法である。

  　　            　　■点の反転■

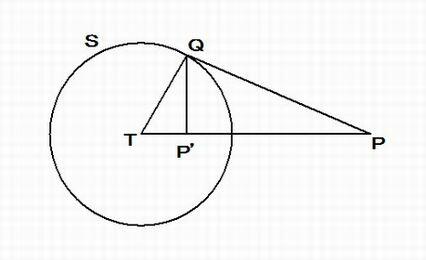
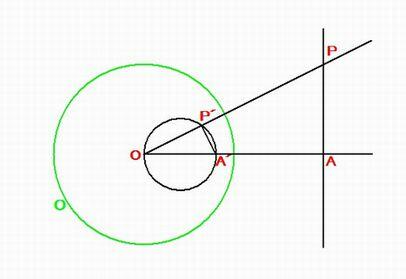
  平面上の定点 Ｔ を中心として、半径 k の円 S があるとき、平面上の T 以外の任意点 P に対して、TP を結ぶ直線上に点P'を

                                        TP･TP' = k^2 ・・・・・・ �@    注）･　は、積（掛け算）の意味です。

となるようにとるとき、P' を円 S に関する Ｐ の 反点 といい、P を Ｐ’ に対応させる 反転 といいます。

 また、このときに使った円 S を 反転の円、その中心 T を 反転の中心、円 S の半径 k を 反転の半径 , k^2を 反転係数といいます。

 

下図に示すように点 P が円 S の外部にあるときは、P から円 S に引いた接線 PQ の接点 Q から直線 TP に引いた垂線の足をP'とすると、

　　　　　　

  　　 　∠TQP =∠TP'Q = 90°, ∠PTQ = ∠QTP'

したがって                                 

  �儺QP ∽�儺P'Q

よって                         

  　TP : TQ = ＴQ : TP' , TQ = k 

から 

                                       TP ･TP' = TQ^2 = k^2 　

したがって、�@が成り立っています。

また、点 P が円 S の内部にあるときは、P の反点 P' は S の外部にあって、同様にして�@が成り立ちます。

★補足★　上式の�@は、｢k が２つの線分の長さ TP と TP' の相乗平均（かけ算してルートを取ったのが相乗平均です）になっている｣ことを示しています。

　　■円の反転■

　【定理A】

　　反転の中心 T を通らない円 C の反転は円 C' である。

【証明】 

 

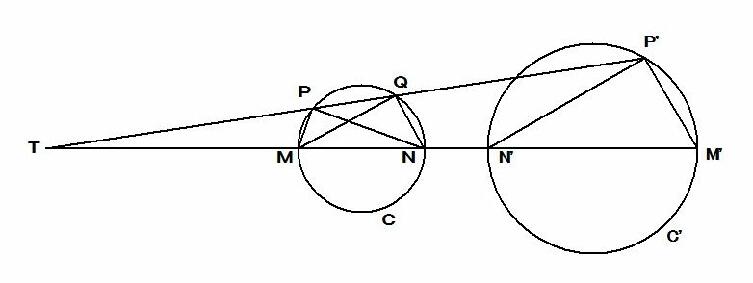
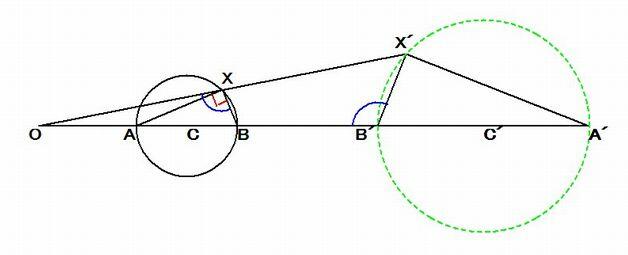
　点 T を反転の中心、反転の半径を k とする。 上図のように、反転の中心 Ｔ を通らない円 C の直径の両端 M, N の反点をそれぞれ M', N' とすると、

M', N' は定点である。 このとき、円 C 上の M, N 以外の任意の点 P の反点を P' とすると TM ・TM' =.TP ・TP' (=k^2)

したがって、4点 M, M', P', P は同一円周上にあるから 　 ∠MPT =∠MM'P'  

また、直線 TPP' と円 C との交点で、P 以外の交点を Q とすると、4点 M, N, Q, P は同一円周上にあるから

　　　　　　　　　　 ∠MPT =∠MNQ したがって　 ∠MM'P' =∠MNQ ・・・・・・ �@

同様にして

　　　　　　　　　　 TN・TN' =.TP・TP' (=k2)　

したがって、4点 N, N', P', P は同一円周上にあるから　　　 ∠NPQ =∠M'N'P' 

また、4点 M, N, Q, P は同一円周上にあるから

　　　　　　　　　　 ∠NPQ =∠NMQ　　したがって ∠M’N'P' =∠NMQ ・・・・・・ �A

よって、　�@と�Aから　�儁NQ ∽�儂'M'P'　

ここで、線分 MN は円 C の直径であるから　∠N'P'M' =∠MQN = 90°

したがって、点 P の反点 P' は線分 M'N' を直径とする円 C' の周上にある。

　ゆえに、反転の中心 T を通らない円 C の反転は１つの円 C' である。 （証明終わり）

  　【定理B】

　反転の中心 T を通る円 C の反転は、T を通らない直線となる。

 

                             

   

【証明】

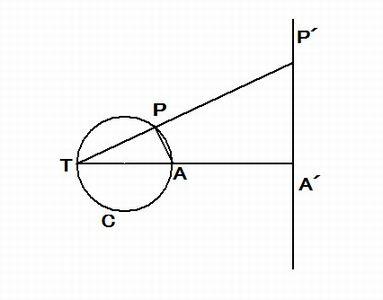
 点 T を反転の中心、反転の半径を k とする。 右の図のように、反転の中心 Ｔ を通る円 C の直径 TA の端点 A の

反点を A' とすると、A' は定点である。 このとき、円 C 上の T, A 以外の任意の点 P の反点を P' とすると 

　　　　　　　　　　　 TA・TA' = TP・TP' (= k2)

したがって、4点 A, A', P', P は同一円周上にあるから

　　　　　　　　　 　 ∠TPA =∠AA'P'  

ここで、線分 TA は円 C の直径であるから　∠TPA = 90°

したがって、∠AA'P = 90° から、点 P の反点 P' は点 Ａ’ を通り ＴＡ に垂直な直線 C' 上にある。

　ゆえに、反転の中心 T を通る円 C の反転は、T を通らない直線 C' である。 （証明終わり）

【補足1】　直線は反転の中心 Ｔ を通る円に反転されます。

【補足2】　反転円の中心 T を通る直線の反転は、やはり点 Ｔ を通る直線となります。

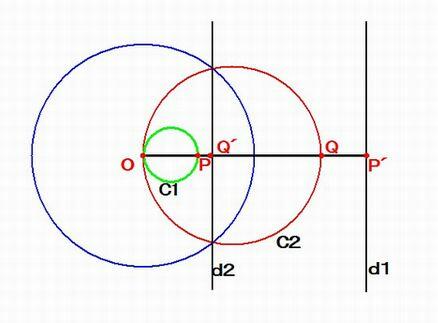
【補足3】　反転の中心 Ｔ で接する２個の円は、点 T を通らない２本の平行な直線に反転されます。

 　　　　　　　　　　

 【定理C】

　反転の中心 T を通らない半径 r の円 C が半径 ｒ' の円 C' に反転されるとき、点Ｔ と円 C の中心 O との中心距離を

 を ｄ とすると、次の等式が成り立つ。        

  r' = r k2 / (d2−r2)

【証明】 

　　　

 

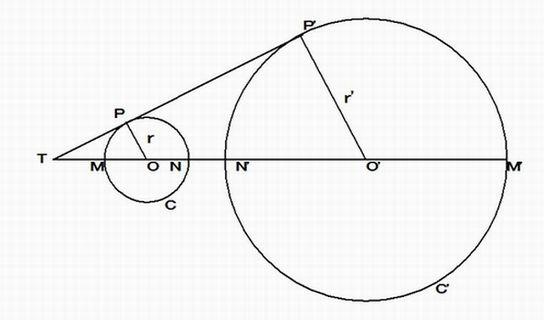
　点 T を反転の中心、反転の半径を k とする。 上の図のように、反転の中心 Ｔ を通らない円 C の中心を O の反点を O' 、T から円 C

 に引いた接線の接点 P の反点を P' とすると、点 P' は円 C' の接点となる。

　このとき、反転の条件式 TM・TM' = TN・TN' = k＾2 　から  

　　　　　　　　　 TM = k＾2/ TM' , TN = k＾2/ TN'  

したがって　　　

  2r' = N'M' = TM'−TN' =　k2/ TM − k2/ TN　

  = k2 (1/TM−1/TN) 

  = k2 (TN−TM) / TM・TN ・・・・・ �@ 

ここで、方べきの定理 によって

     

  TM ・TN = TP2 = TO2 −OP 2

したがって、TN−TM = MN = 2r , TO=d , OP= r と �@ から

　　　　　　　　　　2r' = 2r ・k2/ (d2−r2)  

ゆえに  

　　　　　　　　　　 r' = r k2 / (d2−r2)　 （証明終わり） 

 

 【補足】　この 定理C は、円 C の半径 r から反転円 C' の半径 r' の値を求めるのに便利です。

【定理Ｄ】

　反転の中心 T を通らない半径 r の円 C が半径 ｒ' の円 C' に反転されるとき、点 T から円 C' への接線の長さを L とすると、次の等式が成り立つ。

  r = r' k^2 / L^2

 

【証明】 r = r' k^2 / L^2

 

　点 T を反転の中心、反転の半径を k とする。 定理D の証明で用いた上の図のように、反転の中心 Ｔ を通らない円 C の中心を O の反点を O' 、T 

から円 C に引いた接線の接点 P の反点を P' とすると、点 P' は円 C' の接点となる。

このとき、反転の条件式 TM・TM' = TN・TN' = k^2 　から 

　　　　　　　　　 TM = k2/ TM' , TN = k2/ TN'  

したがって　　　

  2r = MN = TN−TM =　k2/ TN' − k2/ TM'　

  = k2 (1/T'N'−1/TM')  

  = k2(TM'−TN') / TM'・TN' ・・・・・ �@ 

 

ここで、方べきの定理によって

  TM' ・TN' = TP'^2 = L^2 

したがって、TM'−TN' = M'N' = 2r' と TP' = L と �@ から

　　　　　　　　　　2r = 2r' ・k~2/ t'^2 

ゆえに

　　　　　　　 　 　r = r' k^2 / L^2　（証明終わり）

　 OからC，C'までの接線の長さがそれぞれ 

  _______________　　＿＿＿＿__＿

  √OC^2 - r^2, √OC'^2 - r'^2 である．かつ接点も反転の関係なので積はｐ^2である． よって 

                ________________ _________________

  r/r' =  √OC^2 - r^2 ／√OC'^2 - r'^2 = ｐ^2/(OC'^2 - r'^2)

　■ 定理 F ■　

 ２円C1,C2 が点Oで内接または外接するとき、円Oを反転円とする反転変換I(O)によるC1,C2の

反形はともに、C1,C2の共通接線と平行な直線である。

【証明】

             

円Ｃ１の直径ＯＰ，円Ｃ２の直径ＯＱであるように点Ｐ，Ｑをとる． 円Ｏが反転円である反転変換による，点Ｐ，Ｑの逆点をそれぞれＰ’，Ｑ’とすれば， 

円Ｃ１の反形はＰ’を通りＯＰ’に垂直な直線であり，円Ｃ２の反形は Ｑ’を通りＯＱ’に垂直な直線である． 2円Ｃ１，Ｃ２の共通接線はＯを通りＯＰに

垂直な直線であるから 定理F が成り立つ． 

  ■ 反転とその応用 ■

                 

 〔命題〕 反転円が 円O である反転変換で

(1) O を通る直線は、同じ直線に写る。

(2) O を通らない直線は、O を通る円に写る。

(3) O を通る円は、O を通らない直線に写る。

(4) O を通らない円は、O を通らない円に写る。

　   

 【証明】

 

(1) 明らかです。

(2) 点ＡはＯから与えられた直線に下ろした垂線の足で，Ａの逆点がＡ’，およびＯＡ’が直径の円が書いてあります．

 Ｐが直線上の点で，ＯＰと円とのＯ以外の交点をＰ’としたとき 

△ＯＡＰ∽△ＯＰ’Ａ’より

ＯＰ・ＯＰ’＝ＯＡ・ＯＡ’＝（円Ｏの半径）２

が成り立ちます．

したがって（２）が成り立ちます。

(3) 与えられた円の直径をＯＡ’とし，Ａ’の逆点をＡとし，Ａを通りＯＡに垂直な直線を書く．Ｐ’が 与えられた円上の

点で，直線ＯＰ’と直線との交点をＰとすれば，（２）と同様に ＯＰ・ＯＰ’＝ＯＡ・ＯＡ’＝（円Ｏの半径）２

が成り立つので（３）が成り立ちます． 

(4) 反転変換の中心Oを通らない円をCとする．この円の中心CとOを通る直線と円Cの交点をA,Bとし， 反転変換I(O)

によるA,Bの像をそれぞれA´,B´、A´B´を直径とする円をC´とする．

X∈C（Xは C に含まれない）のとき必ずI(O)(X)∈C´ を示せばよい．

   

 すなわち ∠A´X´B´=90° を示せばよい．

I(O)(X)=X´とおく． OA´*OA´=OX*OX´ より

△OAX ∽ △OX´A´ ∴∠OXA=∠OA´X´

OB´*OB´=OX*OX´ より

△OBX∽△OX´B´ ∴∠OXB=∠OB´X´

したがって， ∠A´X´B´=∠AXB

∠AXB=90° より∠A´X´B´=90°

点XがABを直径とする円上にあるから，X´はA´B´を直径とする円上にある. 

　　　　　　　　　　　　　　　　　　　■ 反転法による算額問題 ■

　　　　　　　　　　　　　　　　【新勝寺額堂に奉納された算額の問題】

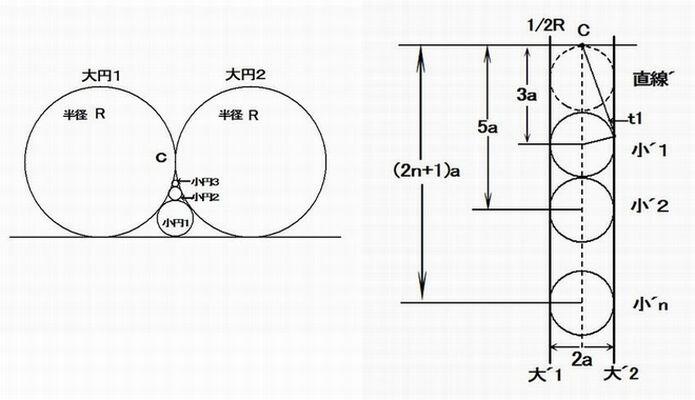
半径 R の２個の大円とそれに接する直線との間に小円を逐次入れて行く。最初の小円を第1円とするとき

ｎ番目の半径 r(n) を求めよ。

                                                                  

　　【反転法による解法】

等しい大円どうしの接点 C で反転すると右の反転図となる。

反転像の小´円の半径を ａ とすると　　ａ = 1/(2R) ・・・�@

C から各小´円への接線の長さ　ｔｎ は　

ｔ1^2 = (3ａ)^2 - ａ^2

ｔ2^2 = (5ａ)^2 - ａ^2

  ・

　　　　　・

ｔｎ^2 = ((2ｎ+1)ａ)^2 - ａ^2

 

反転基本式で、円径に半径を用いると r = (1/(t^2))ａ     

　   

 r1 = ａ/((3ａ)^2 - ａ^2)

 r2 = ａ/((5ａ)^2 - ａ^2)

  ・

　　　　　・

 ｒｎ = ａ/(((2ｎ+1)ａ)^2 - ａ^2) = 1/((4ｎ^2 + 4ｎ)ａ) = 2R/4ｎ(ｎ + 1)

 

　∴　ｎ 番目の小円半径は　　 ｒｎ = R/2ｎ(ｎ + 1) である。

　　　　　　　　　　【 京都・北野天満宮に奉納された算額の問題・・・算額は現存していません 】

  【問題】 

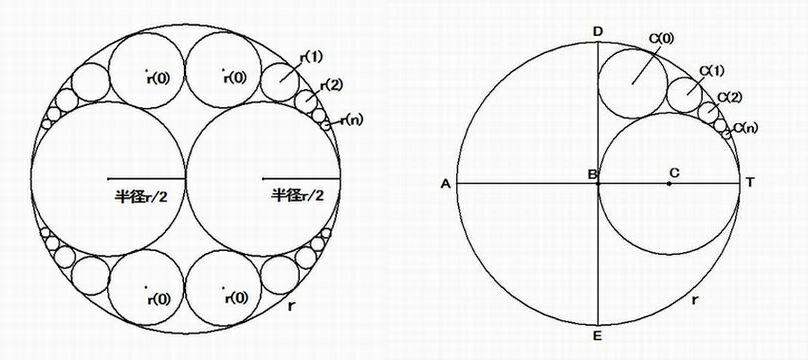
下の図 に示すように、対称的に4つの同じ大きさの半径の円の鎖（くさり）｛r(k) ｝( k= 0, 1, 2, ・・・, n) が半径 r/2 の2つの円に外接し、

半径 r の大円に内接している。このとき r(n) は、つぎのように表されることを証明せよ。 

　　　　　　　　　　　　r(n) = r / { n(n＋2√2)＋4 } 

  【図１：算額の図(現代用)】 　 【図２：簡略図】       

           

点B は最初の大円の中心でその半径はr 、 点C は半径 r/2 の円の中心です。また、点C(k) ( k= 0,1, 2, ・・・, n ) は連続的に外接する円の中心で、

その半径はr(n) です。 

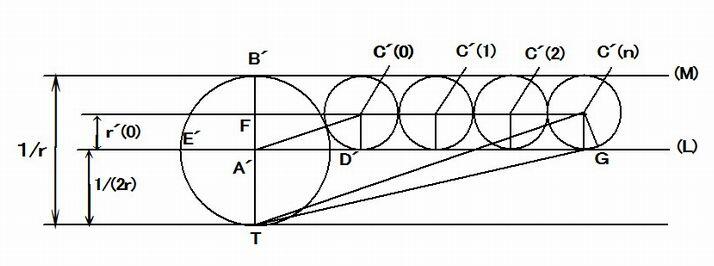
  【図３：簡略図の反転図】

      

　簡略図の反転図 は、つぎのように構成されている。

(a) TA=2r , TA･TA' = k^2, k＝1 から TA' = 1/TA = 1/(2r) である。したがって、【図２】の反転の中心T を通り、

  直径TA=2r の大円は、【図３】では、点A' を通り、TA' に垂直な直線 （L） に反転されている。

(b)　同様にして、TB=r , TB' = 1/TB = 1/r であることから、 【図２】の反転の中心T を通る、直径TB=r の円は、

　　【図３】では、点B' を通り、TB' に垂直な直線 （M）に反転されている。

(c)　上記の�@と�Aで示した２直線 （L） と（M） は平行である。

(d) 【図２】の反転の中心T を通らない線分DBEは、【図３】では、線分TB' を直径とする円の半円部分D'B'E' に

　　反転されている。

(e)　【図２】の点C(0) を中心とする円は、半径 r の大円に内接し、半径 r/2 の円に外接し、線分DBEに接していること

　　から、点C(0) を中心とする円の反転は、【図３】では、2直線 （L）, （M） に接する、点C'(0) を中心とする円である。

(f) 【図２】の点C(1) を中心とする円は、半径 r の大円に内接し、半径 r/2 の円に外接し、点C(1) を中心とする円に

　　外接していることから、 点C(1) を中心とする円の反転は、 【図３】では、点C(1) を中心とする円に外接し、平行な

　　2直線 （L）, （M）にも接する、点C’(1) を中心とする円である。

(g)　上記の�Dと�Eから、【図３】の点C'(i) ( i = 0, 1, 2, 3, …, n ) を中心とする、連続的に外接する円の半径は 

　　r'(i) ( i = 0, 1, 2, 3, …, n ) はすべて等しい。

  　 すなわち r'(0) = r'(1) = r'(2)= ・・・ =　r'(n)　が成り立つ。　

　【図３】において A'C'(0) = 2・r'(0) + r'(0) = 3・r'(0) したがって △A'FC'(0) で  

 FC'(0)^2 = A'C'(0)'^2−A'F^2 = (3・r'(0))^2−r'(0)^2　= 8・r'(0)^2 よって　FC'(0) = 2√2・r'(0)

　ここで、 r'(0) = r'(1) = r'(2) = ・・・ = r'(n) であるから  

　FC'(n) = FC'(0)＋C'(0)C'(n) = 2√2・r'(0)＋2n・r'(0) = 2(n＋√2)・r'(0)  

　したがって △TFC'(n) で　

  (TC'(n))^2 = TF^2＋(FC'(n))^2 = (3・r'(0))^2＋4(n＋√2)^2・r'(0)^2 = 9・r'(0)^2＋4(n＋√2)^2・r'(0)^2

　よって △TGC'(n) で TG = L とおくと、 C'(n)G＝ｒ’(n)=r(0) から

  L^2 = TC'(n)'^2−C'(n)G^2 = ｛9・r'(0)^2＋4(n＋√2)^2・r'(0)^2｝− r'(0)^2 

  = 8・r'(0)^2 ＋4(n＋√2)^2・r'(0)^2 = ｛(n＋√2)^2＋2｝・4r'(0)^2

　ここで、　2・r'(0) = A'B' = TB' − TA' = 1/r − 1/2・r = 1/2・r から r'(0) = 1/4・r  

　ゆえに、前節で示した【定理D】によって

  r(n) = r'(n) / L^2 = r'(0) / {(n+√2)^2+2}・4r'(0)^2 = 1/ { (n+√2)^2+2 }・4r'(0) = r / { n(n+2√2)+4 }

 

　　                                           　　■ 反転基本式 ■

原点を通らない円は原点を通らない円に反転される。 ただし, それらの円の中心を通る直線は原点を通る. 反転する

前の円の半径をr, 反転した後の半径をr′, 原点から反転した後の円への接線の長さをt′ とすると

    r = (K^2/(t´^2)) r′  が成り立つ. これを基本式とする。

                  

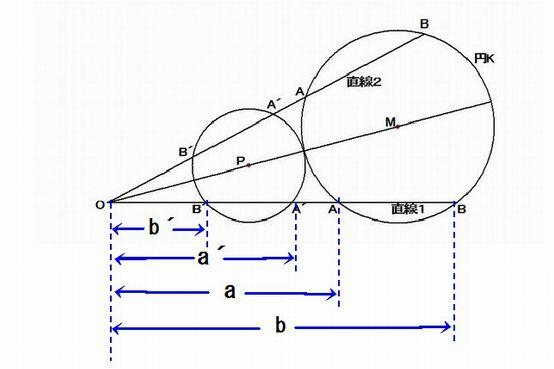
中心がM, 半径r の円K をおく.O を通る任意の直線１と円K の交点をA,B また点A,B を反転した点をA´,B´ とする。

O からA,B,A´,B´ の各点までの長さをａ,ｂ,ａ´,ｂ´ とすると定義より ａａ´ = k^2, ｂｂ´ = K^2

またO から円K に引いた接線の長さをt とすると, 方べきの定理より ａ´/ｂ = ｂ´/ａ = ｂｂ´/ａｂ = K^2/ｔ^2 = 一定

A´ を通り直線BM に平行な直線はOM と交わる点を P としてOM = ｍ,OP = P ,MB = r, PA´ = r ´とすると,

△OPA´ ∽ △OMB の関係から

P/m = a´/b = r´/r = K^2/t^2 より P = (K^2/t^2)m = 一定 r′ =(K^2/t^2)r = 一定

以上のことにより円K の反転像は中心がP, 半径がr´ の円になることがわかる。

また, 反転された円への接線の長さをt´とすると, 

定義より　tt´ = K^2 より 　r = (t^2/K^2)r´ = (K^2/t´)^2・(1/K^2)r = (K^2/t´^2) r´となる。