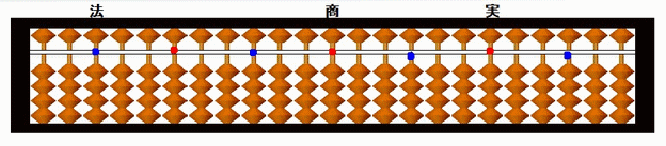
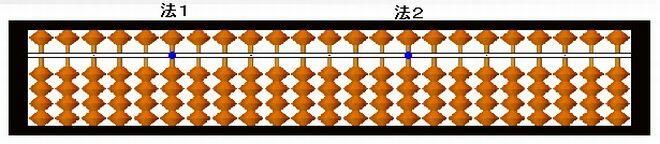
偦傠偽傫丂暋棙寁嶼
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亂屲忔崻亃
乮倎亄倐乯^5亖倎^5+5倎^4倐+10倎^3倐^2+10倎^2倐^3+5倎倐^4+倐^5 亖倎^5+倐(5倎^4+10倎^3倐+10倎^2倐^2+5倎倐^3+倐^4)
丂丂丂丂丂丂
亂扨棙朄偲暋棙朄亃
乽扨棙朄乿偲偼丄摉弶梐偗偨尦杮偵懳偟偰偺傒棙懅偑偮偒傑偡丅棙懅傪嵞塣梡偡傞偙偲偼偟傑偣傫丅
乽暋棙朄乿偼偙傟偲偼堎側傝丄摉弶梐偗偨尦杮偵偮偄偨棙懅傪偳傫偳傫尦杮偵慻傒擖傟偰怴偨側尦杮偲偟丄棙懅傪嵞塣梡偡傞曽朄偱偡丅
偙偺偨傔丄棙懅偑尦杮偵慻傒崬傑傟丄尦杮帺懱偑戝偒偔側偭偰偄偒傑偡丅
亂扨棙朄偺寁嶼亃
扨棙朄偺寁嶼偱偼 丂a(1+nr)=b a(1+nr)=b 偑惉棫偡傞
偨偩偟丆a 偼尦嬥丆r 偼擭棙棪丆n 偼擭悢丆b 偼 n 擭宱夁帪偺嬥妟丅
弶婜忬懺丗尦嬥 a
1擭宱夁帪偺嬥妟丗乽尦嬥亄偙偺1擭偱憹偊偨棙巕偺傇傫乿偱丆a+ar=a(1+r)
2擭宱夁帪偺嬥妟丗乽1擭宱夁帪偺嬥妟亄偙偺1擭偱憹偊偨棙巕偺傇傫乿偱丆a(1+r)+ar=a(1+2r)
摨條偵峫偊傞偙偲偱丆 n 擭屻偺嬥妟偼丆 b=a(1+nr)
亂暋棙朄偺寁嶼亃
暋棙朄偺寁嶼偱偼丂 a(1+r) n =b a(1+r)n=b 偑惉棫偡傞丅
偨偩偟丆a 偼尦嬥丆r 偼擭棙棪丆n 偼擭悢丆b 偼 n 擭宱夁帪偺嬥妟丅
弶婜忬懺丗尦嬥 a
1擭宱夁帪偺嬥妟丗乽尦嬥亄偙偺1擭偱憹偊偨棙巕偺傇傫乿偱丆a+ar=a(1+r)
2擭宱夁帪偺嬥妟丗乽1擭宱夁帪偺嬥妟亄偙偺1擭偱憹偊偨棙巕偺傇傫乿偱丆
a(1+r)+a(1+r)r =a(1+r) 2 =a(1+r)丱2
3擭宱夁帪偺嬥妟丗乽2擭宱夁帪偺嬥妟亄偙偺1擭偱憹偊偨棙巕偺傇傫乿偱丆
a(1+r) 丱2 + a(1+r)丱2r=a(1+r)丱3
摨條偵峫偊傞偙偲偱丆 n 擭屻偺嬥妟偼丆 b=a(1+r) ^n
椺)俆愇傪5擭戄偟丄侾俀丏係係侾俇愇庢傞偲偒偼丄擭棙壗妱偺棙懅偵側傞偐丅
丂仸愇(偙偔)偼梕検偺扨埵偱丄1愇偼10搇亖100彙亖栺180儕僢僩儖丅暷1愇偺廳偝偼栺140乣150kg丅
丂仸奜壗妱丒丒丒尦杮偺懠偵丄壗妱偐偺棙懅丂尦杮傪侾侽偲偡傞偲偒丄棙懅偼俀丄尦棙崌寁偼侾俀偱偁傞
丂丂 撪壗妱丒丒丒尦杮偺撪偵丄壗妱偐偺棙懅丅尦杮傪俉偲偡傞偲偒丄棙懅偼俀偲側傞丅尦棙崌寁偼侾俀偱偁傞丂
丂丂丂丂丂丂丂丂丂奜俀妱傪撪偵捈偡偲丂俀 亐 俉丂亖 侽丏俀俆丂偲側傞丅乮棙棪偼俀妱俆暘乯
嘆杮棙偲傕偵侾俀丏係係侾俇偲抲偒丄俆愇偵偰妱傟偽俀丏係俉俉俁俀偲側傞丅偙傟傪幚偵抲偔丅
嘇弶彜偵侾偲棫偰丄朄偱侾傪俆搙妡偗崌偄丄幚偐傜堷偗偽侾丏係俉俉俁俀偲側傞丅
嘊乽師偺彜偵丂侽丏俀乿傪棫偰傞丅朄偵乽弶彜 侾乿傪係搙妡偗崌偄丆俆攞偟偰 俆丂傪朄偵抲偔丅丂
仭倐(5倎^4+10倎^3倐+10倎^2倐^2+5倎倐^3+倐^4)丂
0.2(5x1^4 + 10x1^3x0.2 + 10x1^2x0.2^2 + 5x1x0.2^3 + 0.2^4)
嘋乽弶彜 侾乿傪俁搙妡偗崌偄丆侾丂偲乽師偺彜丂侽丏俀乿傪妡偗丄侾侽攞偟偨 俀 傪朄偵壛偊傞丅丂
嘐乽弶彜 侾乿傪俀搙妡偗崌偄丆侾丂偲乽師偺彜丂侽丏俀傪俀搙妡偗崌偄偟偨 侽丏侽係乿傪妡偗丄侾侽攞偟偨 侽丏係 傪朄偵壛偊傞丅丂

5x1x0.2^3 + 0.2^4 丂5倎倐^3+倐^4)
嘑乽弶彜 侾乿 偲乽師偺彜丂侽丏俀傪俁搙妡偗崌偄偟偨 侽丏侽侽俉乿傪妡偗丄侾侽攞偟偨 侽丏侽係 傪朄偵壛偊傞丅丂
嘒朄偺 俈丏係係侾俇 偲 乽師偺彜丂侽丏俀乿傪妡偗崌偄 侾丏係俉俉俁俀 偲惉傞丅
嘓朄偺俈丏係係侾俇 傪幚傛傝堷偒丄幚傪 侽 偲偡傞丅彜偺丂侾丏俀 偱丄奜俀妱 偑媮傔傞夝偱偡
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亂尰戙偺曽朄偱夝傪媮傔傞亃
俀丏係俉俁俀 偺屲忔崻傪媮傔傛丅
丂丂 丂丂丂丂丂丂丂丂丂 丂丂 ______________________
嘆 乽彫悢揰傪婎弨乿偵偟偰乽俀寘偢偮乿嬫愗偭偰偄偔丅 丂丂 5併俀丏鶸係俉鶸俉俁鶸俀
嘇 堦斣嵍偺悢偼俀偱丄俆忔偟偰 俀 傛傝彫偝偄惍悢 侾 傪媮傔傞丅
嘊 侾^5亖侾傪俀傛傝堷偒丄侾傪弌偡丅侾偺墶偵忋偺傪壓傠偟丄係俉俉俁俀 傪嶌傞丅
丂丂 丂丂丂 __侾__鶸俀_______________
丂丂 丂丂丂 5併俀丏鶸係俉鶸俉俁鶸俀
倎^5 丂 丂丂 丂丂丂 侾
-------------------------- 丂丂丂 丂 丂丂丂丂 --- 鶸------------
倐(5倎^4+10倎^3倐+10倎^2倐^2+5倎倐^3+倐^4)丂傛傝丂倐=0.2丂偲偡傞丅 侾 鶸係俉鶸俉俁鶸俀
0.2(5x1^4 + 10x1^3x0.2 + 10x1^2x0.2^2 + 5x1x0.2^3 + 0.2^4) 丂 侾 鶸係俉鶸俉俁鶸俀
-------------------------- 丂丂丂 丂 丂丂丂丂 --- 鶸------------丂丂丂丂丂丂
丂 丂丂丂丂 丂丂丂丂丂丂丂丂丂丂丂丂侽
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 丂丂丂丂丂丂丂丂丂
丂亪丂俀丏係俉俁俀 偺屲忔崻 偺棫曽崻偺夝偼丂侾丏俀_偱偡丅
丂丂丂丂丂丂丂丂丂丂丂丂丂 丂仧乽嶼朄鑽媈彺乿戞2姫乽奐棫朄乿偵婰嵹偝傟偨椺戣仧
悺乮侾悺亖栺 30.303 mm乯扨埵偺懱愊偑丂侾俉俇侽丏俉俇俈捸乮侾捸亖栺3.305 78m2乯偁傞丅
偙傟傪奐棫偡傟偽堦曈偺挿偝偼丄偄偐傎偳偐丠
仭乽奐棫朄乿偵偍偗傞丄偦傠偽傫忋偺昞婰仭
乽朄乿丒丒丒暘曣偺悢偵偁偨傞傕偺丅
乽彜乿丒丒丒妱傝嶼偺寢壥丅
乽幚乿丒丒丒暘巕偺悢偵偁偨傞傕偺丅
亂奐棫朄偺埲壓偺戙悢幃揥奐傪梡偄傞亃
a^3+倐乮俁倎^2亄俁倎倐亄倐^2乯+們乷俁乮倎亄倐乯^2亄俁乮倎亄倐乯們亄們^2乸
丂丂
嘆幚偵丂侾俉俇侽丏俉俇俈 偲抲偔乷乽乽彫悢揰傪婎弨乿偵偟偰乽俁 寘偢偮乿嬫愗偭偰偄偔丅侾鶸俉俇侽.鶸俉俇俈丅 埵傪尒偰丂
嘇傑偢愮偺埵偺侾傛傝丂乽堦偺埵偺彜丂10悺乮堦広乯乿偑棫偮丅
丂仭 a^3亖侾丂傛傝丂倎亖侾
嘊乽堦偺埵偺彜乿傪俁忔偟偰侾侽侽侽捸傪彜傛傝堷偔丄巆傝 俉俇侽丏俉俇俈
嘋傑偢乽擇偺埵偺彜偵丂俀乿傪棫偰傞丅朄侾偵乽堦偺埵偺彜 侾侽乿傪俀忔偟偰丆俁妡偗偟偰 俁侽侽丂傪朄侾偵抲偔丅丂
丂
丂仭倐乮俁倎^2亄俁倎倐亄倐^2乯丂傛傝丂(3x10^2+3x10x倐+倐^2)x倐=(300+30x倐+倐^2)x倐 亝 侾俉俇侽丏侽俉俇俈
倐=俀偺応崌丂(300+30x2+2^2)x2= 728
倐=3偺応崌丂(300+30x3+3^2)x3= 1197 丒丒丒 俉俇侽 傪挻偊傞堊丂丂倐=俀 偲偡傞
嘍乽堦偺埵偺彜丂侾侽乿偲乽擇偺埵偺彜丂俀乿傪妡偗崌偄 俀侽 傪丄俁妡偗偟偰 俇侽丂傪朄侾偵壛偊傞丅
乽擇偺埵偺彜丂俀乿傪俀忔偟偰丆係 傪朄侾偵壛偊丄朄侾傪 俁俇係 偲偡傞丅
嘐乽擇偺埵偺彜丂俀悺乿傪朄侾偲妡偗崌偄丄朄侾傪 俈俀俉 偲偡傞丅
嘑師偵乽擇偺埵偺彜偵丂俁乿傪棫偰傞丅朄俀偵乽堦偺埵偺彜 侾侽乿傪俀忔偟偰丆俁妡偗偟偰 俁侽侽丂傪朄俀偵抲偔丅丂
嘒乽堦偺埵偺彜丂侾侽乿偲乽擇偺埵偺彜丂俁乿傪妡偗崌偄 俁侽 傪丄俁妡偗偟偰 俋侽丂傪朄俀偵壛偊傞丅
乽擇偺埵偺彜丂俁乿傪俀忔偟偰丆俋 傪朄俀偵壛偊丄朄俀傪 俁俋俋 偲偡傞丅
嘓乽擇偺埵偺彜丂俁悺乿傪朄侾偲妡偗崌偄丄朄俀傪 侾侾俋俈 偲偡傞丅幚偺 俉俇侽 傪挻偊傞堊
乽擇偺埵偺彜乿丂傪丂俀悺偲偡傞丅朄侾偺 俈俀俉丂傪幚傛傝堷偒丄幚傪 侾俁俀俉俇俈 偲偡傞丅
嘔傑偢乽嶰偺埵偺彜偵丂俀乿傪棫偰傞丅朄侾偵乽堦偺埵偺彜 侾侽侽 偵擇偺埵偺彜丂俀侽乿傪壛偊丄俀忔偟偰乮侾俀侽亊侾俀侽乯偐傜
丂俁妡偗偟偰 係俁俀侽侽丂傪朄侾偵抲偔丅丂丂
丂
丂仭們乷俁乮倎亄倐乯^2亄俁乮倎亄倐乯們亄們^2乸傛傝丂丂乷3(100+20)^2+3(100+20)C+C^2乸xC=乷3(120)^2+3(120)C+C^2乸xC=
乷3(14400)+360C+C^2乸xC=(43200+360C+C^2)xC
C=俀偺応崌 (43200+720+4)x俀=87848
C=俁 偺応崌 (43200+1080+9)x3=13286 丒丒丒侾俁俀俉俇俈 偲摍偟偄堊丂丂C=俁 偲偡傞
嘕乽堦偺埵偺彜 侾侽侽 偵擇偺埵偺彜丂俀侽乿傪壛偊 侾俀侽 傪丄俁妡偗偟偨 俁俇侽丂傪乽嶰偺埵偺彜 俀乿攞丂俈俀侽 傪
丂丂朄侾偵壛偊傞丅 乽嶰偺埵偺彜丂俀乿傪俀忔偟偰丆係 傪朄侾偵壛偊丄朄侾傪 係俁俋俀係 偲偡傞丅
嘖朄侾傪乽嶰偺埵偺彜 俀乿攞偟偨 俉俈俉係俉 傪朄侾偵抲偔丅
嘗師偵乽嶰偺埵偺彜偵丂俁乿傪棫偰傞丅朄俀偵乽堦偺埵偺彜 侾侽侽 偵擇偺埵偺彜丂俀侽乿傪壛偊丄俀忔偟偰乮侾俀侽亊侾俀侽乯偐傜
丂俁妡偗偟偰 係俁俀侽侽丂傪朄俀偵抲偔丅丂丂(43200+1080+9)x3=13286俈丂們乷俁乮倎亄倐乯^2亄俁乮倎亄倐乯們亄們^2乸
嘙乽堦偺埵偺彜 侾侽侽 偵擇偺埵偺彜丂俀侽乿傪壛偊 侾俀侽 傪丄俁妡偗偟偨 俁俇侽丂傪乽嶰偺埵偺彜 俁乿攞丂侾侽俉侽 傪
丂丂朄俀偵壛偊傞丅 乽嶰偺埵偺彜丂俁乿傪俀忔偟偰丆俋 傪朄俀偵壛偊丄朄俀傪 係係俀俉俋 偲偡傞丅
嘚乽嶰偺埵偺彜丂俁悺乿傪朄侾偲妡偗崌偄丄朄俀傪 侾俁俀俉俇俈 偲偡傞丅幚偺 侾俁俀俉俇俈 偲摍偟偄堊
乽嶰偺埵偺彜乿丂傪丂俁悺偲偡傞丅
嘜朄俀偺 侾俁俀俉俇俈丂傪幚傛傝堷偒丄幚傪 侽 偲偡傞丅彜偺丂侾俀丏俁 悺偑丄媮傔傞夝偱偡
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亂尰戙偺曽朄偱夝傪媮傔傞亃
丂侾俉俇侽丏俉俇俈 偺棫曽崻傪媮傔傛丅
丂
乮倎亄倐乯^2= a^2+2ab+b^2 亪c{俁乮倎亄倐乯^2}=3a^2c+6abc+3b^2
丂乮倎亄倐亄們)^3=.a^3+3a2b+3ab^2+b^3+3a^2c+6abc+3b^2c+3ac^2+3bc^2+c^3=
a3+倐乮俁倎^2亄俁倎倐亄倐^2乯+們乷俁乮倎亄倐乯^2亄俁乮倎亄倐乯們亄們^2乸
丂丂 _____________________
嘆 乽彫悢揰傪婎弨乿偵偟偰乽俁寘偢偮乿嬫愗偭偰偄偔丅 剎併侾鶸俉俇侽.鶸俉俇俈 丂
丂丂
嘇 堦斣嵍偺悢偼侾偱丄俁忔偟偰 侾偺棫曽崻偺庱埵侾 傪媮傔傞丅
嘊 侾^3亖侾 傪侾傛傝堷偒丄侽 傪弌偡丅侽偺墶偵忋偺俉俇侽傪壓傠偟丄侽俉俇侽 傪嶌傞丅
丂
丂丂丂 __侾鶸________________
丂丂丂 剎併 侾鶸俉俇侽.鶸俉俇俈
倎^3 丂丂丂 丂侾鶸
-------------------------- 丂丂丂 --- 鶸----------------------
丂 丂 侽鶸俉俇侽鶸
嘋 倐乮俁倎^2亄俁倎倐亄倐^2乯傛傝丂丂(3x10^2+3x10x倐+倐^2)x倐=(300+30x倐+倐^2)x倐 亝 侾俉俇侽丏侽俉俇俈
倐=俀偺応崌丂(300+30x2+2^2)x2= 728
倐=3偺応崌丂(300+30x3+3^2)x3= 1197 丒丒丒 俉俇侽 傪挻偊傞堊丂丂倐=俀 偲偡傞
丂丂丂 __侾鶸____俀鶸_________________________________
丂 丂剎併 侾鶸俉俇侽.鶸俉俇俈
倎^3 丂丂 侾鶸俉俇侽 鶸
-------------------------- 丂丂 --- 鶸----鶸------------------
倐乮俁倎^2亄俁倎倐亄倐^2乯 丂丂丂丂 侽鶸俉俇侽鶸
鶸俈俀俉鶸
-------------------------- 丂丂 --- 鶸----鶸------------------
丂丂丂 鶸侾俁俀鶸俉俇俈
嘍 們乷俁乮倎亄倐乯^2亄俁乮倎亄倐乯們亄們^2乸傛傝丂丂乷3(100+20)^2+3(100+20)C+C^2乸xC=乷3(120)^2+3(120)C+C^2乸xC=
乷3(14400)+360C+C^2乸xC=(43200+360C+C^2)xC
C=俀偺応崌 (43200+720+4)x3=87848
C=俁 偺応崌 (43200+1080+9)x3=13286 丒丒丒侾俁俀俉俇俈 偲摍偟偄堊丂丂C=俁 偲偡傞
丂丂丂 __侾鶸____俀鶸_____俁___
丂丂丂 剎併 侾鶸俉俇侽.鶸俉俇俈
倎^3 丂丂丂 侾鶸俉俇侽 鶸
-------------------------- 丂丂 --- 鶸----鶸------------------
倐乮俁倎^2亄俁倎倐亄倐^2乯 丂丂丂丂 侽鶸俉俇侽鶸
鶸俈俀俉鶸
------------------------- 丂丂丂 --- 鶸----鶸------------------
丂們乷俁乮倎亄倐乯^2亄俁乮倎亄倐乯們亄們^2乸丂丂丂 丂丂 丂鶸侾俁俀鶸俉俇俈
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 丂丂丂丂丂丂 鶸侾俁俀鶸俉俇俈
------------------------- 丂丂 --- 鶸----鶸------------------丂丂丂丂
侽
丂亪丂侾俉俇侽丏俉俇俈 偺棫曽崻偺夝偼丂侾俀丏俁丂偱偡丅






 5x1x0.2^3 + 0.2^4 丂5倎倐^3+倐^4)
5x1x0.2^3 + 0.2^4 丂5倎倐^3+倐^4)