【関孝和 円周率の計算】 

円周率は、円に内接する正多角形の周の長さをもとに、円周率の近似値をつくります。関は1681年頃に正13万1072角形を用いて

小数第11位まで求めました。 関はこの時、効率よく計算する方法を編み出しています。円に内接する正2 ^n角形のnを一つずつ

増やしていく時に、周の長さが等比数列になるという法則（エイトケン加速）を発見していました。

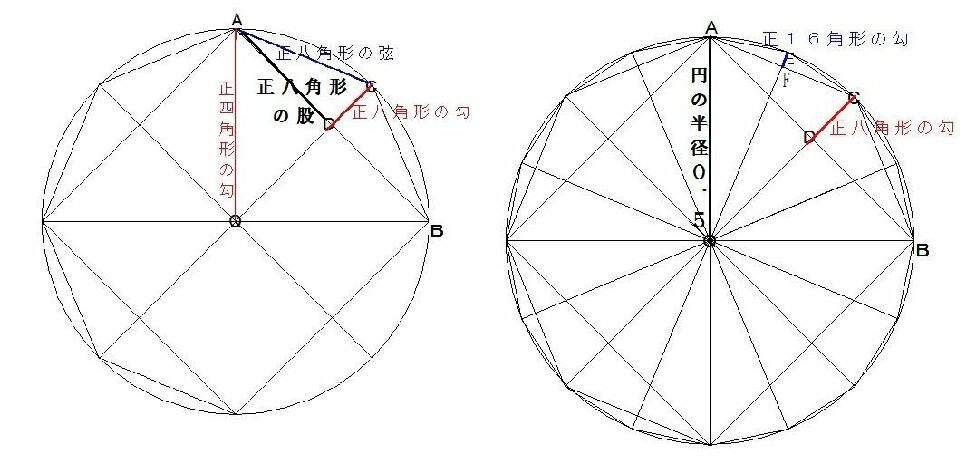
 円周率を求めるには、直径１尺の円に正四角形を内接させ、次に正八角形、正１６角形,最後に

正１３１０７２角形を内接させる。正多角形を内接すると、図のように、直角三角形が生ずる。

直角を挟む短い辺を「勾」、長い辺を「股（こ）」、斜辺を「弦」と名付けます。

　 　　  

   　

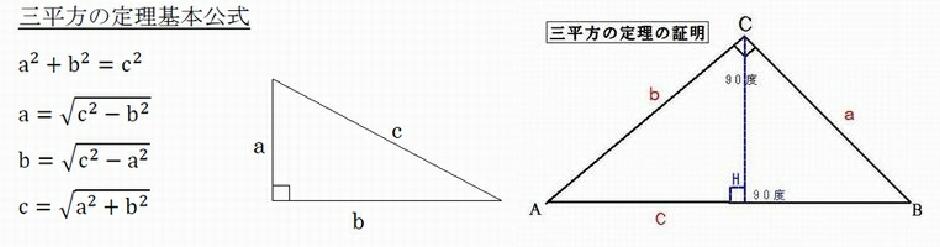
　｛三平方の定理の証明｝

  △ＡＢＣと△ＡＣＨが相似だから　ｂ：ＡＨ ＝　Ｃ：ｂ .・・ｂ^2　＝　ＡＨＣ・・ＡＨ　＝　ｂ^2　÷　Ｃ

 　△ＡＢＣと△ＣＢＨが相似だから　ａ：ＢＨ ＝　Ｃ：ａ.・・ａ^2　＝　ＢＨＣ・・ＢＨ　＝　ａ^2　÷　Ｃ

  Ｃ　＝　ＡＨ　＋　ＢＨ　＝　ｂ　÷　Ｃ　＋　　ａ^2　÷　Ｃ・・ａ^2　＋　ｂ^2　＝　Ｃ^2

 　　　　｛三平方の定理（和算では勾股弦の定理）を使って、円周率を求める｝

正四角形の勾 ＝ ＡＱ ＝ ０．５　 正四角形の股 ＝ ＢＱ ＝０．５　

　　　　　　　　　　　　　 　 _______________________________________________　　______________________　　　________　　　

正四角形の弦 ＝ ＡＢ ＝　√正四角形の勾^2 ＋ 正四角形の股^2＝ √0.5^2　＋　0.5^2 ＝ √０．５

 

★正四角形の周の長さ｛円周率｝ ＝ ４×√0.5 ＝ 2.82842712475　

正八角形の股 ＝ ＡＤ ＝ ＡＢ／２　＝ 　√0.5／ ２　( 0.35355339059) 　　　　　　

　　　　　　 　　 　　 　 　　 　＿_____________________ ＿___________________________         

正八角形の勾 ＝ 0.5 − ＤＱ ＤＱ ＝ √AＱ^2　−　AＤ^2 ＝ √0.5^2− (√0.5／ ２)^2  

  ______________________ ___________________________________    

  ＝ √ 0.25− 0.125 = √ 0.125 = 0.35355339059 勾 ＝ 0.5 − 0.35355339059  = 0.14644660941 

  _______________________________________________

正八角形の弦 ＝ ＡＣ ＝√正八角形の勾^2　＋　正八角形の股^2 ＝           

  __________________________________________________ ___________________________________________

√0.14644660941^2 ＋ 0.35355339059^2 ＝ √0.0214466094 ＋ 0.12499999999 ＝ 0.38268343234

  　             

★正八角形の周の長さ｛円周率｝ ＝ ８×0.38268343234　＝ 3.06146745872 　　　

  　　　　　　     

正16角形の股 ＝ ＡF ＝ ＡC／２　＝ 正八角形の弦／ ２　＝ 　0.19134171617　　　　　　　　　　　　　　　　　　　　 　　　　 

  _________________________________________ ______________________________________   

正16角形の勾 ＝ 0.5 −√円の半径^2 − 正16角形の股^2 ＝ √ 0.5^2 − 0.19134171617^2  

  ______________________                                         

  = √0.21338834765 = 0.46193976625 勾 ＝ 0.5 − 0.46193976625 = 0.03806023375 

  ________________________________________________

正16角形の弦 ＝ ＡＣ ＝√正16角形の勾^2　＋　正16角形の股^2 ＝

  ______________________________________________________　 　 ________________   

 √0.038060023375^2 ＋ 0.19134171617^2 ＝ √0.03806021772 ＝0.19509028094

             

★正16角形の周の長さ｛円周率｝ ＝ １６×0.19509028094　＝ 3.12144449504           

正32角形の股 ＝ 正16角形の弦／ ２　＝ 　0.09754514047　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　 　　    

  __________________________________________ ______________________________________   

正32角形の勾 ＝ 0.5 − √円の半径^2　−　正32角形の股^2 ＝ √ 0.5^2 − 0.09754514047^2  

  ______________________                                        

  = √0.24048494557 = 0.49039264428 勾 ＝ 0.5 − 0.49039264428 = 0.00960735572

  ________________________________________________ 

正32角形の弦 ＝ ＡＣ ＝√正32角形の勾^2　＋　正32角形の股^2 ＝            

 　_____________________________________________________ ___________________                     

 √ 0.00960735572^2 ＋ 0.09754514047^2 ＝ √0.00960735571 ＝0.09801711947

             

★正３２角形の周の長さ｛円周率｝ ＝ ３２×0.09801711947　＝ 3.13654782304