【原文の要約】

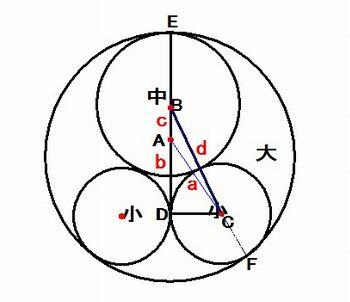
　図のように大円の内側に中円1箇と小円2箇を互いに接するように内接させます。いま、中円1箇と小円2箇の面積を除く,

外余積が120歩、小円の直径が中円の直径より5寸短いとするとき、大、中、小円の直径をそれぞれ求めなさい。

 

  大円径 = L、中円径 = M、小円径 = Sとする。　中円径と小円径の差 = M − S 、外余積 = π/4(L^2−M^2−S^2) とする。

π/4(円周率/4)は円積率と呼ばれますが、これは円の面積を直径で求めたことに関係します。

外余積は、大円の面積から、中円と小円の面積を引いた残り。

円の直径の2乗から円の面積を求める。

円の面積は半径×半径×π

直径の2乗を計算してみましょう。

 直径×直径 = (半径×2)×(半径×2) = 半径×半径×4

結果を比べると、半径×半径の係数がπか4かの違いだけのようですね。

πは定数ですから、直径の2乗が円の面積と比例し、π/4だけ違ってる。

π/4は円積率と呼ばれますが、これは円の面積を直径で求めたことに関係します。

           

 図で、2つの直角三角形の辺の長さに着目して、

 

 a = L/2 ― S/2 d = M/2 + S/2 ∴ 2d = M + S

 　 【 AD(b)の長さを求める 】

 b^2 = a^2 - (S/2)^2 = (L/2 ― S/2)^2 - (S/2)^2 = (L/2)^2 - 2(L/2)(S/2) = L^2/4 - 2LS／4) = (L^2 - 2LS)／4)

  ＿＿＿＿＿＿

  b = (√(L^2 - 2LS))／2　

 は、 4b^2 = (2a)^2 - S^2 = (L ― S)2 - S2 = L^2 - 2LS 　 4b^2 = L^2 - 2LS　

　((L - S)／2)^2 = b^2 + (S/2)^2 

　　 【 BA(c)の長さを求める 】

  　　　　　　　　　　　　　　　　　 　＿＿＿＿＿＿　　　　　　＿＿＿＿＿＿

 c = L/2 - M/2 = BD - b = (√(M^2 + 2MS))／2 - (√(L^2 - 2LS))／2

∴　2c = L - M    4c^2 = L^2 - 2LM + M^2

　　 【 BD(c + b)の長さを求める 】

 BD^2 = (c + b)^2 = d^2 - (S/2)^2 = (M/2 + S/2)^2 - (S/2)^2 = (M/2)^2 + 2(M/2)(S/2) = M^2/4 + 2MS／4 =

  ＿＿＿＿＿＿

 (M^2 + 2MS)／４　  BD（c + b) = (√(M^2 + 2MS))／2 

 KM = AM - AK = KB -MB　であるから 　　 【 BA(c)の長さを求める 】

  　　　　　　　　　　　　　　　　　 　＿＿＿＿＿＿　　　　　　 ＿＿＿＿＿

 c = L/2 - M/2 = BD - b = (√(M^2 + 2MS))／2 - (√(L^2 - 2LS))／2 　

  __________________ ________________ __________________ _________________

 L - M = (√(M^2 + 2MS)) - (√(L^2 - 2LS)) (L - M)^2 = ((√(M^2 + 2MS)) - (√(L^2 - 2LS)))^2

  _________________________________

 L^2 - 2LM + M^2 = M^2 + 2MS - 2(√((M^2 + 2MS)(L^2 - 2LS))) + L^2 - 2LS

 

  __________________________________

 LM + MS - LS = √((M^2 + 2MS)(L^2 - 2LS))

  ___________________________________

 ((LM + MS) - LS)^2 = (√((M^2 + 2MS)(L^2 - 2LS))) ^2

 

 ((LM + MS)^2 - 2LS(LM + MS)) + LS^2 = (M^2 + 2MS)(L^2 - 2LS)

 ((LM + MS)^2 - 2LS(LM + MS)) + LS^2 = M^2(L^2 - 2LS) + 2MS(L^2 - 2LS)

 

 4LM^2S + M^2S^2 - 4L^2MS + 2LMS^2 + L^2S^2 = 0

S^2(M^2 + 2LM + L^2) = 4S(L^2M - LM^2) ・・・　両辺を S で割る。

 S(M^2 + 2LM + L^2) = 4(L^2M - LM^2)

 

   　　　　　■ 条件を整理し、解を得る ■

 (1) S(M^2 + 2LM + L^2) = 4(L^2M - LM^2)

 (2) M - S = 5 M = S + 5

 (3) ４外余積(4 * 120 = 480) = V = π(L^2 - M^2 - 2S^2)   V/π = π/π(L^2 - M^2 - 2S^2) = L^2 - M^2 - 2S^2

 (3)　より　　L^2 = α = V/π + M^2 + 2S^2 = V/π + (S + 5)^2 + 2S^2 = V/π + 3S^2 + 10S + 25

 

  【 (1) の処理を行う 】 .  

S((S + 5)^2 + 2L(S + 5) + L^2) = 4(L^2(S + 5) - L(S + 5)^2)

S((S^2 + 10S + 25) + 2L(S + 5) + L^2) = 4(L^2(S + 5) - L(S^2 + 10S + 25))

S^3 + 10S^2 + 25S + 6LS^2 + 50LS - 3L^2S = 20L^2 - 100L

6LS^2 + 50LS + 100L = 20L^2 + 3L^2S - S^3 - 10S^2 - 25S

6LS^2 + 50LS + 100L = L^2(20 + 3S) - S(S + 5)^2 ・・・　両辺を2乗する。

((6LS^2 + 50LS) + 100L)^2 = ( (L^2(20 + 3S)) - (S(S + 5)^2) )^2

((6LS^2 + 50LS)^2 + 2*100L(6LS^2 + 50LS) + (100L)^2 = (L^2(20 + 3S))^2 - 2S((S + 5)^2*(L^2(20 + 3S)) +

(S(S + 5)^2)^2

36L^2S^4 + 600L^2S^3 + 3700L^2S^2 + 10000L^2S + 10000L^2 = 400L^4 + 120L^4S + 9L^4S^2 - 2L^2S(20S^2 +

200S +500 + 3S^3 + 30S^2 + 75S) + ((S^3)^2 + 2S^3*10S^2 + (10S^2)^2 + 2*25S(S^3 + 10S^2) + (25S)^2  

L^2(36S^4 + 600S^3 + 3700S^2 + 10000S + 10000) - S^6 - 20S^5 - 150S^4 - 500S^3 - 625S^2

= L^2(400L^2 + 120L^2S + 9L^2S^2 - 100S^3 - 550S^2 -1000S - 6S^4)

(3) より L^2 = α = V/π + 3S^2 + 10S + 25 V/π = 480/π ≒ 152.7887　とする。 ∴　 L^2 = 3S^2 + 10S + 177.7887　　

　

(3S^2 + 10S + 177.7887)(36S^4 + 600S^3 + 3700S^2 + 10000S + 10000) - S^6 - 20S^5 - 150S^4 - 500S^3 - 625S^2

 = (3S^2 + 10S + 177.7887)(21S^4 + 350S^3 + 3450.0983S^2 + 24334.644S + 71115.48)

 

  【 左辺 の処理を行う 】

(3S^2(36S^4 + 600S^3 + 3700S^2 + 10000S + 10000) + 10S(36S^4 + 600S^3 + 3700S^2 + 10000S + 10000)

+ 177.7887(36S^4 + 600S^3 + 3700S^2 + 10000S + 10000) - S^6 - 20S^5 - 150S^4 - 500S^3 - 625S^2

107S^6 + 2140S^5 + 23350.3932S^4 + 173173.22S^3 + 787193.19S^2 + 1877887S + 1777887

  【 右辺 の処理を行う 】

 (3S^2 + 10S + 177.7887)(21S^4 + 350S^3 + 3450.0983S^2 + 24334.644S + 71115.48)

 = 3S^2( 21S^4 + 350S^3 + 3450.0983S^2 + 24334.644S + 71115.48) + 10S( 21S^4 + 350S^3 + 3450.0983S^2 +

 24334.644S + 71115.48) + 177.7887(21S^4 + 350S^3 + 3450.0983S^2 + 24334.644S + 71115.48)

 = 63S^6 + 1260S^5 + 17583.8576S^4 + 169730.96S^3 + 1070081.37163S^2 +5037579.52172S + 12643528.7391

  【 上記の解より、両辺 の処理を行う 】

107S^6 + 2140S^5 + 23350.3932S^4 + 173173.22S^3 + 787193.19S^2 + 1877887S + 1777887

= 63S^6 + 1260S^5 + 17583.8576S^4 + 169730.96S^3 + 1070081.37163S^2 +5037579.52172S + 12643528.7391

107S^6 - 63S^ + 2140S^5 - 1260S^5 + 23350.3932S^4 - 17583.8576S^4 + 173173.22S^3 - 169730.96S^3 +

787193.19S^2 - 1070081.37163S^2 + 1877887S - 5037579.52172S + 1777887 - 12643528.7391 = 0

44S^6 + 880S^5 + 5766.5356S^4 + 3442.26S^3 - 282888.18163S^2 - 3159692.52172S -10865641.7391 = 0

  【 六次方程式 で、S（小円） を求め,解を得る 】

 

 S = 7.586875355　　　　　M = S + 5　より　　M = 7.586875355 + 5 = 12.586875355

  480/3.1415926 = 152.788747975 152.788745368

(3) より L^2 = α = V/π + 3S^2 + 10S + 25 V/π = 480/π ≒ 152.7887　とする。 ∴　 L^2 = 3S^2 + 10S + 177.7887　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 _____________________

 L^2 = 3(7.586875355)^2 + 10(7.586875355) + 177.7887 = 426.339486507 　L = √426.339486507 = 20.6479898902

４外余積(4 * 120 = 480) より 解を検証する。 π = 3.1415926・・・とする。　

V(４外余積) = π(L^2 - M^2 - 2S^2) = 3.1415926（20.6479898902^2 - 12.586875355^2 - 2*7.586875355^2) = 479.99984928

∴ 解は　　　大円(L) = 20.6479898902 中円(M) = 12.586875355 小円(S) = 7.586875355