 |
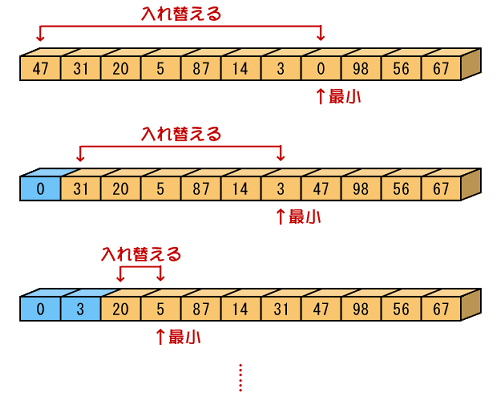
| 図.1 比較と交換を分離したソートアルゴリズム |
|---|
今回もソートです。バブルソートを発展させて、別のアルゴリズムを考えてみましょう。
では、今回の要点です。
では、いってみましょう。
前回のバブルソートでは、最大のものを探しつつ同時に交換も行っていました。が、今回はこれを分けてみたいと思います。そして、今回は最小のものを最初に持っていくようにします。
つまり、先ず最小のものを探し、それを最初のものと交換するということになります。次は、それを除いた範囲で最小のものを探し、それを最初から2番目のものと交換します。
図にすると、こんな感じです。
 |
| 図.1 比較と交換を分離したソートアルゴリズム |
|---|
こうすると、交換の回数がぐっと減ります。交換はなかなかに時間のかかりそうな処理なので、それが減るのは心強いですね。
このように、最小のものを最初に持っていくようなソート法を、選択法と呼びます。
では、プログラムを作ってみましょう。
| プログラム |
|---|
// Sort2.cpp
#include "SortData.h"
#include "SortSub.h"
// 選択法
void SelectSort(int* pnData, int nNumOf)
{
int iLoop; // (データの個数−1)回回すための変数
int iSearch; // 一番小さいのを探すときのループ変数
int iMin; // 一番小さいデータのインデックス
int nMin; // 現在の最小データ
// (データの個数−1)回回す
for(iLoop = 0; iLoop < nNumOf - 1; iLoop++)
{
// 初期値の代入
iMin = iLoop;
nMin = pnData[iLoop];
// 一番小さいデータを探す
for(iSearch = iLoop + 1; iSearch < nNumOf; iSearch++)
{
// より小さいデータがあると、iMin と nMin を更新する
if(pnData[iSearch] < nMin)
{
iMin = iSearch;
nMin = pnData[iSearch];
}
}
// データの移動
Swap(pnData[iMin], pnData[iLoop]);
}
}
int main()
{
SelectSort(g_anData, g_nNumOf);
DispArray(g_anData, g_nNumOf);
return 0;
} |
| 実行結果 |
1, 1, 4, 6, 9, 9, 10, 11, 13, 14, 15, 16, 23, 25, 28, 29, 31, 33, 34, 39, 39, 40, 40, 41, 42, 44, 48, 51, 51, 53, 54, 55, 56, 63, 67, 68, 73, 73, 76, 77, 78, 79, 79, 87, 89, 99, 99, 101, 101, 103, 110, 112, 116, 117, 117, 118, 124, 128, 136, 137, 137, 138, 148, 150, 152, 155, 157, 160, 161, 164, 166, 167, 168, 169, 173, 173, 174, 175, 185, 186, 188, 192, 199, 203, 213, 215, 222, 228, 228, 229, 231, 235, 239, 240, 240, 242, 249, 249, 254, 255, |
はい、きちんとソートできましたね。
交換の回数が少ない分、選択法はバブルソートよりも高速です。選択法も作るのは簡単なので、自作するときは選択法を使った方がいいかもしれませんね。
では、今回の要点です。
それでは次回まで。
Last update was done on 2000.9.13
この講座の著作権はロベールが保有しています