
「ペラ焼き」の行列解消法は購入する枚数で列を2つに分ける方法です。今回はちょうど鉄板が2つだったので1つの鉄板の列は2枚以下、もう1つの鉄板の列は3枚以上とすれば少ない購入枚数の列は早く買えるようになると思います。
本当に早くなるのかどうか、表を使って検討してみます。
まず A の表を説明します。行列が40人いるところから考えます。2枚購入する人と3枚購入する人が交互に並んでいるとします。鉄板は2つで、それぞれ3枚ずつが同時に焼けることにします。5回焼けるたびに新たに12人が行列に加わるとします。これも2枚購入と3枚購入の人が交互に並んで増えます。これを1サイクルとしましょう。
1サイクルで焼けるのは、
3枚(1つの鉄板で1度に焼ける枚数)×2つ(鉄板の数)×5回(1サイクルで焼き上がる回数)
=30枚
です。
そして1サイクルで増える人数が必要とする枚数は
5枚(2枚+3枚)×6組(2枚購入と3枚購入の2人を1組とする)=30枚です。
1サイクルで焼ける枚数と新たに行列に加わる人が必要とする枚数が同じなので、行列の人数は全く変わりません。

それでは列を2つにします。1つの列は2枚購入する人が並びます。もう1つの列には3枚購入する人が並びます。それぞれの列に1つの鉄板とします。 こちらも先ほどと同じように40人の行列から始めますが、列が2つなので、20人ずつとなります。
1サイクルごとに増える人数はそれぞれの列に6人ずつです。1サイクルで焼ける枚数も同じ30枚ですし、新たに行列に加わる人が必要とする枚数も30枚で同じ条件です。
2枚購入の列が B の表で、3枚購入の列が C の表です。 B と C をまとめたものが D の表です。
2枚購入の列では、1サイクルで焼けるのは 3枚×5回=15枚 で、1サイクルで増える人が必要とする枚数の 2枚×6人=12枚 より多いので、行列は減っていきます。逆に3枚購入の列では新たに増える6人が18枚(3枚×6人=18枚)を必要とするので、1サイクルで1人ずつ行列が増えていくことになります。
それで2枚購入の行列が 0人 になると1サイクルで3枚余ることになるので、それは3枚購入の列に回します。
こうして表を見てみると、これまでの方法では行列の人数はずっと28人のままですが、2列に分けた場合は9サイクルが終わった時点で24人まで減っています。この表からは最初の行列が解消するまでは効果があることがわかります。
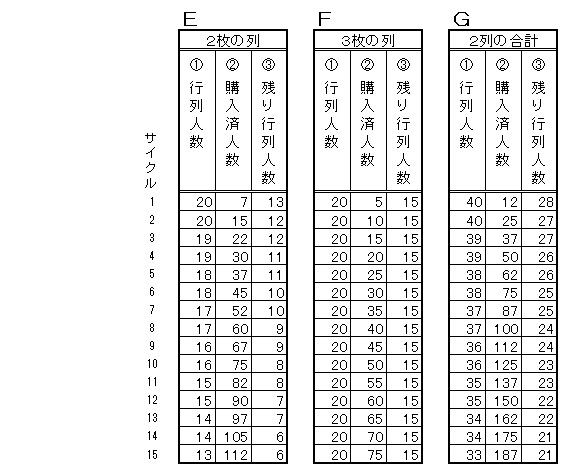
次に E と F の列を説明します。こちらは最初の20人ずつの列までは同じ条件ですが、1サイクルで増える人数を2枚購入は7人、3枚購入は5人とします。両方で増えるのは12人でこれは変わりません。これだと15サイクルが終わった時点で行列は21人まで減っていてさらに減り続けます。B と C の場合より効果が大きくなります。
実際には行列の長さや進み具合を見てどちらの列に並ぶかを考えると思うので、最初は3枚購入しようと思っていた人が2枚に変更してそちらの列に並ぶことが考えられます。
売れ具合によっては1枚だけの列と2枚以上の列にしてもいいですし、最高3枚までとかの制限をすることもできますので十分に効果があると思います。
そうなると売り上げ枚数が減るとも考えられますが、一定の時間で焼ける枚数が決まっているので影響はないと思いますがどうでしょうか。