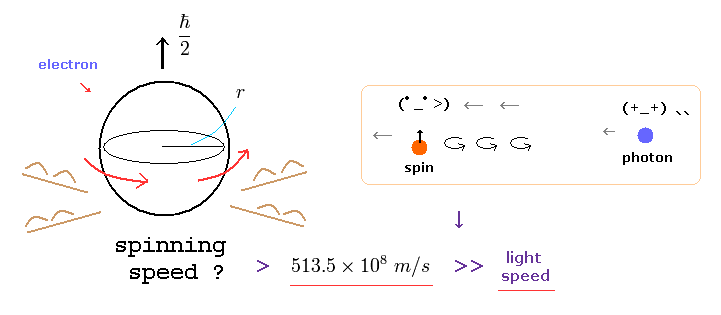
Top page (correct Bohr model including helium )
Derivation of Fermi golden rule and statistics.
Spintronics of condensed matter physics is illusion.
(Fig.1) Spinning speed of an electron is much faster than light !
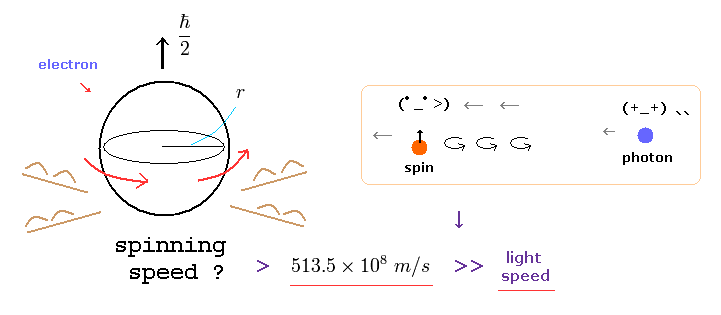
According to actual experiments, a single electrons is a very small point-like particle.
But quantum mechanics insists this point-like electron has 1/2 ħ angular momentum.
As you know, the angular momentum means mv× r ( m= electron mass, v=rotation speed, r is electron radius ).
Considering electron's very small mass and radius, this rotating speed "v" must be more than 100 times light speed to reach 1/2 ħ ! ( See also this page. )
This means quantum mechanical spin is unrealistic and just a fantasy.
(Fig.2) Pauli exclusion principle is a force ? → "Shut up and calculate !"
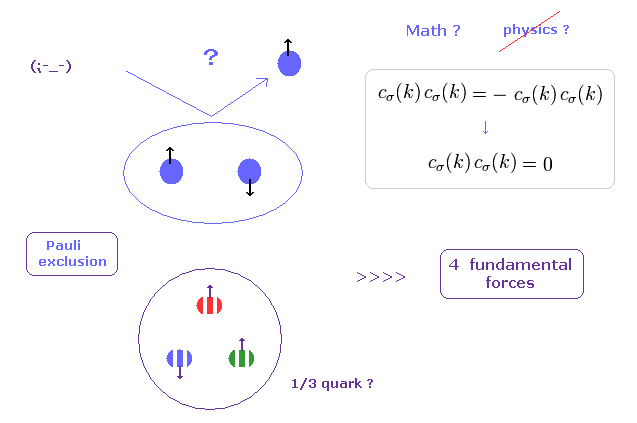
If you see some condensed matter physics textbooks, you would find those books are filled with unrealistic "spins".
Main reason is "Pauli exclusion principle", in which two identical fermions cannot enter in the same place (= state ).
( But I think, this definition of the "same" place is very vague. How can we define these boundary lines ?? )
For example, in 1s energy state, only spin "up" and "down" electrons can exist.
They introduced very artificial "colors" (= red, blue, green ) in quarks to satisfy Pauli exclusion principle by force.
So, the force involved in this mysterious Pauli exclusion principle is much stronger than all other fundamental forces !
The problem is physicists NEVER try to ask what this Pauli exclusion principle really is, even in 21th century now.
Instead of wasting a great deal of money in useless accelerator, they should investigate the true form of this Pauli exclusion, first, I think.
(Fig.3) How "mathematical" operator can describe various phenomena, rich in variety ??
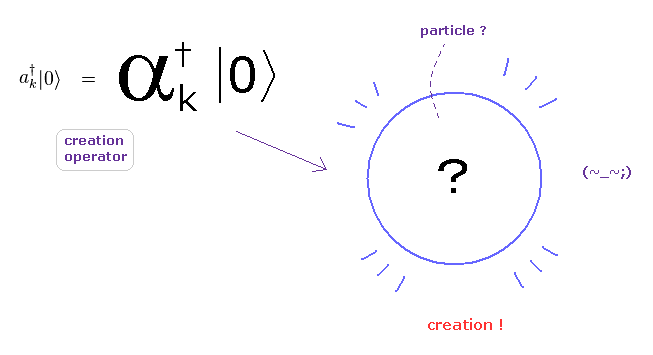
In the present quantum field theories including condensed matter physics, standard model, and string theory, they completely rely on "mathematical" ( NOT physical ) operators to describe various phenomena.
As you see this page, these creation and annihilation operators do NOT have the power to express various dynamic and complicated phenomena in the actual world.
Because, when a particle is created ( or annihilated ), these operators cannot designate various differernt places and times in each different dynamic particle.
So the main obstructions to the development of sicence are these very abstract oparators (and "spin ").
(Fig.4) Real variable world is NOT mathematical and simple operators !
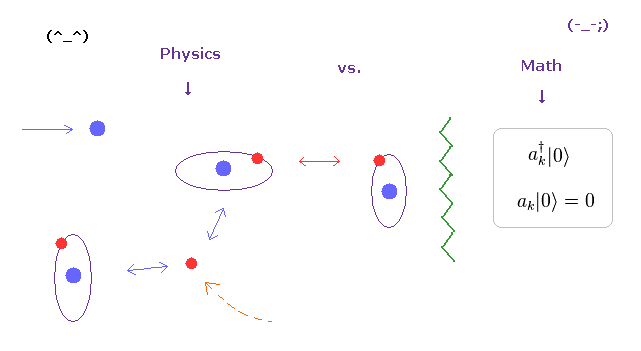
As you see various physical phenomena and complicated mechanism in our human bodies, actual particles such as electrons and protons are moving around , interacting with each other at various different places and times.
For example, when a particle A is approching particle B, other another C is getting away from particle D ....
And various interactive "timing" and positional relationship determine various biological functions, which is rich in variety.
Unfortunately, the present mathematical operators such as "a†" and "a" cannot describe these variable functions at all.
(Fig.5) Spin - spin interaction is unrealistically weak.
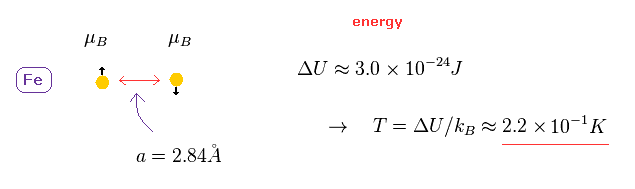
It is said that ferromagnetism is caused by spin-spin interactions in metals.
But this spin magnetic moment is too weak to cause ferromagnetism in room temperature !
The lattice constant of iron is 2.84 Å.
In this distance, the energy difference between parallel and antiparallel spin interactions are too small, as shown in Fig.6.
Using Boltzmann constant k, this energy difference is equal to only 0.22 kelvin. ( See this page. )
So if spin-spn interaction is caused by their magnetic moments, a magnet is easily broken in room temperature !
(Fig.6) Weak "spin" can always turn other spins toward the same ( opposite ) directions ??
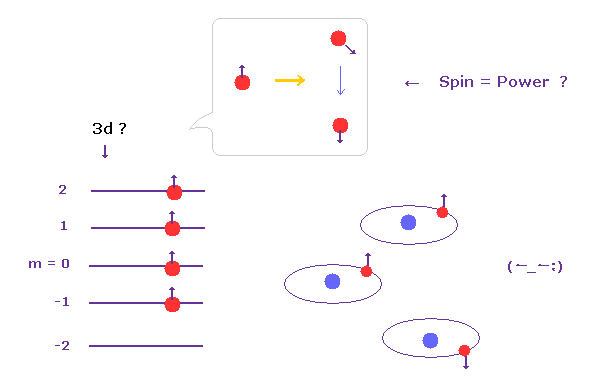
According to this book ( Story of Spin by S.Tomonaga ), the magnetic moment of electron spin is too weak (= fine structure level, 0.00005 eV ).
So these spins don't have the initiative at all, overcoming various Coulomb interactions.
But they try to give imaginary "leadership" to this very weak spin, by force. Why ?
Because as I said, mysterious Pauli exclusion principle is the strongest in all fundamental forces.
And they like various artifical rules in condensed matter physics.
In L-S coupling, when there is little electrons, total angular momentum becomes J = L-S, but at some point, this J suddenly becomes L+S, they insist. ( very "convenient" spin. )
Of course, it is impossible that we confirm these mathematical orbitals and ( rotating )"spin" directly.
(Fig.7) Real spin state ? Point particle ?

In addition to artifial rules, "spin" is precessing, they insist.
So according to quantum mechanics, "real" spin angular momentum is NOT 1/2 ħ !
How point-like spin can precess ?
And why this angle of inclination (= θ ) is constant even in various different magnetic fields ?
This is strange.
(Fig.8) "Mathematical" Phonons = viscosity ??

Superfluidity is a state of matter in which the matter behaves like a fluid with zero viscosity at extremely low temperature.
The problem is that the present quantum theory tries to describe this phenomena using "mathematical" phonons.
"Phonons" are quasiparticles, so they are NOT real.
But the present theories are restricted strictly to very abstract "mathematical" symbols, so they cannot explain what these phonons ( and "spin" ) really are, using clearer objects.
This is the main reason why the present condensed matter physics cannot be developed to express more dynamic nano-phenomena.
(Eq.1) Symmetry breaking ?
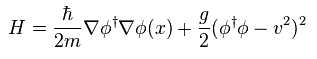
According to the present quantum theory, Higgs potential in non-relativistic field is given by Eq.1.
(Eq.2)

When φ is determined by a fixed value of "v" (= Eq.2 ), this is ground state, and "symmetry" is broken, they insist.
(Eq.3)

They like to introduce very abstact concept such as "phase".
( Though they NEVER try to explain what this "phase" really is. )
When this phase χ(x) includes the position variable "x", energy of Eq.1 becomes higher than the ground state, by
(Eq.4)
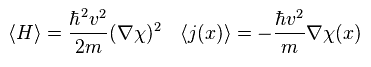
So this ununiformity in the phase χ(x) causes superfluid, they insist.
But as most people feel, it is impossible to describe various variable phenomena and interactions using ONLY these abstract mathematical symbols.
In short, these theories completely lack realistic useful tools.
They are just bound with some mathematical spells.
(Eq.5)

They suddenly introduced Hamiltonian including imaginary "phonons", like Eq.5.
They insist these creation or annihilation operators (= ζ ) mean "phonons", which can cause superconductivity, as if by magic.
The first term means electron's Hamiltonian (= kinetic energy ), and the second term is phonon's energy.
And the third term means the interactive Hamiltonian among electrons and "phonon", they insist.
(Eq.6)
When some electrons have higher energies than a single phonon, they can emit phonon and cause viscosity with other electrons, they insist.
So when each electron has lower energy than a single phonon at extremely low temperature, they cannot interact with each other, which is "superfluid".
Of course, considering these phonons are unreal quasiparticles, they should clarify what these phonons really are, as soon as possible.
(Eq.7)

According to the BCS theory, two negative electrons are attracted toward each other, and form stable Cooper pair, they insist.
Again, they don't try to explain concrete mechanism of this mysterious attraction.
When "g" of the third term of Eq.7 is positive ( g > 0 ), spin up and down electrons can form Cooper pair by attractive interaction, they insist.
(Eq.8)

So Eq.8 is Cooper pair.
But the concrete mechanisms remain unknown even in 21th century now.
This is strange.
Instead of wasting great deal of money in useless accelerator, they should clarify the true form of this phonons as soon as possible, I think.
(Fig.9) Kondo effect doesn't prove "spin" at all.
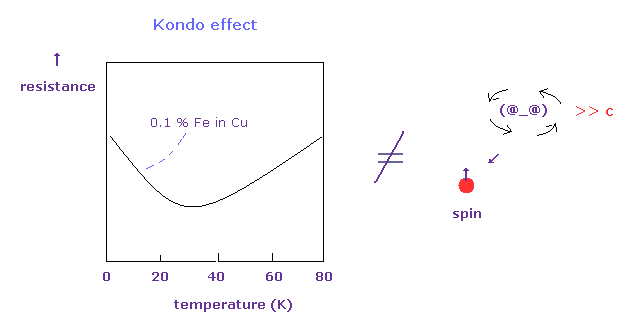
Usually, as temperature becomes lower, the electrical resistance becomes weaker.
But in metals with magnetic impurities ( ex. Cu + 0.1 % Fe ), this resistance becomes stronger at much lower temperature again.
They insist these effects are caused by spin-spin interaction among s and 3d electrons.
But as I say in this section, these theories cannot prove existence of "spin" at all.
And "spin" proves to be only "mathematical" ( NOT physical ) symbols.
(Eq.9) Anderson Hamiltonian.

In Eq.9, c† and c mean creation and annihilation operators of conduction electrons (= s orbital ).
And d† and d mean 3d orbital electrons of a magnetic impurity such as Fe.
( As I said in Fig.3, these very abstract operators cannot express more dynamic electron's behavior. )
The first and second terms mean each independent energy, and the third term means repulsive Coulomb interaction between 3d electrons.
And the fourth term is interactive Hamiltonian between s (= c ) and 3d electrons, they insist.
(Eq.10)
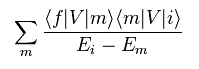
As shown in this page, effective Hamiltonian of second order ( with respect to "V" ) becomes like Eq.10.
"f", "m" and "i" mean "final", "middle" and "initial" states.
(Fig.10) Conduction electron is scatterd by 3d electron into k' state.
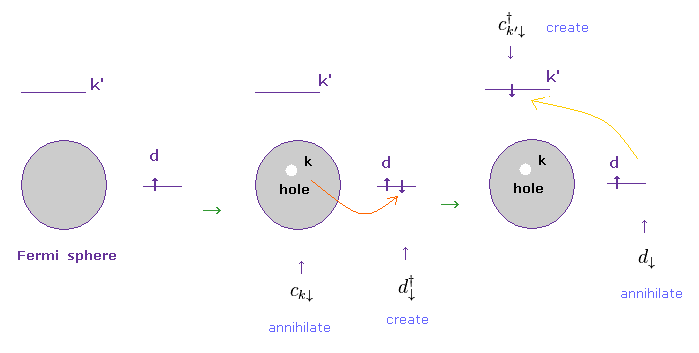
Fig.10 shows the process in which a conduction electron moves from its fermi energy state into 3d orbital, and then, other conductive state (= k' ) by some scattering.
Unfortunately, all they can do is to express these physical process using only very abstract creation and annihilation operators, as shonw in Eq.11.
(Eq.11)
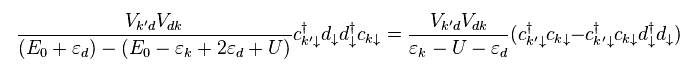
A conduction electron is first annihilated (= c ) in the fermi sphere, and then created (= d† ) in 3d orbital.
After that, this electron is annihilated (= "d" ), and moves into k' state (= created, c† )
Only interactive Hamiltonian "V" of Eq.9 is involved in the numerator.
And when two electrons exist in 3d orbital, the repulsive interaction (= "U" ) appear.
Of course, two electrons in 3d orbital satisfy Pauli exclusion principle.
( But these states are only speculations, and cannot be seen directly, )
(Eq.12)
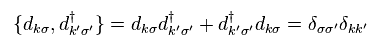
In Eq.11, anticommutation relation of Eq.12 is used.
So as I said above, this anticommulation relation (= Pauli exclusion principle ) has absolute power, in any situation !
Though spin magnetic moment is extremely weak.
(Eq.13)
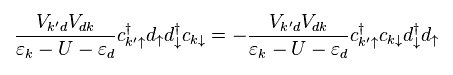
In Eq.13, the final k' electron has "up" spin instead of "down" spin in Eq.11.
In this way, there are total 8 different patterns in this process.
Summing up all patterns of scattering, they get s-d model Hamiltonian of
(Eq.14)
In Eq.14, they change various interactive Vkd into one common form of "V", approximately.
But the most important part is the diversity of this interactive V.
As long as they don't try to investigate concrete dynamic interactive motions of electrons, the present quantum theory cannot escape blind alley.
(Fig.11) "Spin" = Math ?? NO physical reality.
In conclusion, "spin" in various papers in condensed matter physcis and spintronics is just a "mathematical" thing, and has NO physical reality at all.
If they want to describe various scattering, they should use more realistic and concrete models to express them, NOT relying on "abstract" operators.
(Eq.15)
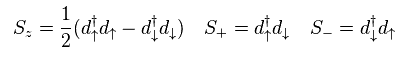
They change 3d electron's operators into spin operator "S".
As you see, they believe "mathematical" spin (= symbol ) blindly.
So in various papers in condensed matter physics, the word of "spin" always appears.
Though they don't try to explain what this "spin" really is.
(Eq.16)
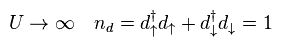
Here they define repulsive Coulomb energy U as infinity.
So the total 3d electron's number in final state becomes "1" ( not "2" ).
Using Eq.15 and Eq.16,
(Eq.17)
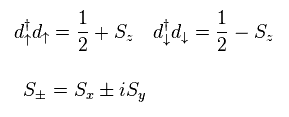
They suppose the energy of conduction electron is much smaller than repulsive U.
And the special energy relation of "particle hole symmetry" is defined, like Eq.18.
(Eq.18)
Here, the following Pauli matrices are used.
(Eq.19)
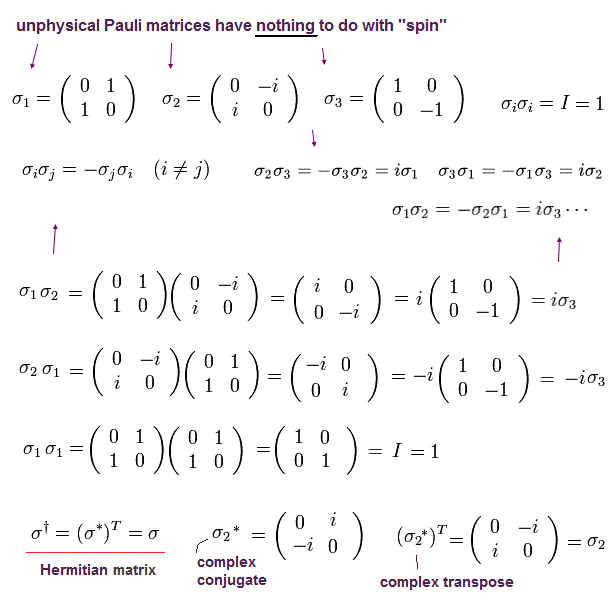
The important point is that "x" (= 1 ) and "y" (= 2 ) components of Pauli matrices contradict quantum mechanics itself.
Because there are only two states (= "up" and "down" spins in "z" ) according to Stern-Gerlach.
So these σx and σy are only mathematical products.
Using Pauli matrices, they change conduction electron's operators, as follows,
(Eq.20)
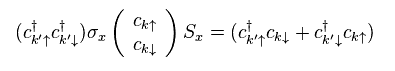
As a result, s-d Hamiltonian of Eq.14 becomes
(Eq.21)
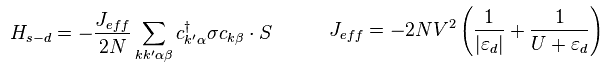
In Eq.21, Jeff is negative, so when the spins of s (= σ ) and d (= S ) electrons are antiparallel to each other,
(Eq.22)
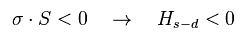
Hamiltonian (= Hs-d ) becomes negative and stable (= Kondo singlet ).
So they insist conduction and 3d electrons have diamagnetism relationships.
Of course, spin magnetic moment itself do NOT have power overcoming various Coulomb forces.
So the relation of Eq.22 is completely unrealistic.
Actually, they cannot show concrete state of " spin ". They only show "mathematical" matrices.
Unfortunately, this is the true figure of "spin" in various spintronics papers.
(Eq.23)

The electric conductivity (= σ(T) ) is defined as J = σ(T) E.
( J = current, E = external electric field ).
In this section, we show this conductivity can be expressed like Eq.23.
In Eq.23, τ means relaxation time.
After this τ, electron's state almost returns to its original state.
"f(ε)" is electron's distribution (= Fermi-Dirac statistics ).
(Eq.24)
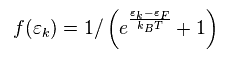
We define electric current j as shown in Eq.25.
"ħk" is momentum "p", and Ω is resistance.
(Eq.25)
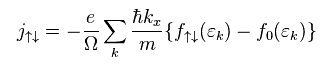
" f↑↓ " and " f0 " represent fermi distributions with or without electric currents, respectively.
They suppose after the relaxation time of τ, "f↑↓" returns to static "f0".
The derivative of f↑↓ with respective to "t" is
(Eq.26)
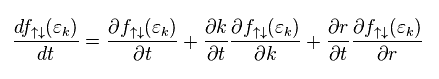
They define current (= state ) as almot constant, so
(Eq.27)
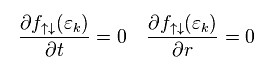
According to Newton law,
(Eq.28)
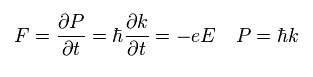
From Eq.26 to Eq.28, the change of state "f(ε)" during the time of τ is
(Eq.29)

where
(Eq.30)

From Eq.25, Eq.29, and Eq.30, the current j becomes
(Eq.31)

where
(Eq.32)
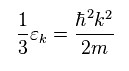
In Eq.31, they change Σ (= sum of "momentums" ) into integration of ε, using probability density of ρ
As a result, they can get conductivity σ of Eq.23.
The transition probability is given by Fermi golden rule, as follows,
(Eq.33)
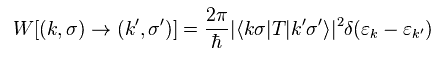
According ot perturbation theory, the transition matrix "T" can be defined as
(Eq.34)
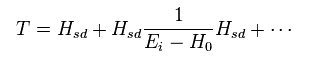
First we think about first-order perturbation with respect to Hsd ( not "V" ) in Eq.34.
( = the first term in Eq.34 right. )
Spin operators satisfy
(Eq.35)

And the relaxation time τ can be defined as
(Eq.36)
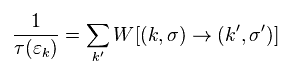
From Eq.21, Eq.33-Eq.36,
(Eq.37)
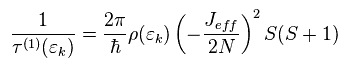
The result of Eq.37 means first-order perturbation (= Born approximation ).
It cannot show the relation between the temperature "T" and conductivity ( or resistance ).
Because temperture "T" doesn't appear.
As shown in the second term of Eq.34 right, the second-order Hamiltonian includes reciprocal of ( E-H ).
This mathematical definition by quantum mechanics leads to the serious divergence in Kondo effects.
(Eq.38)
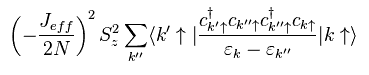
The second term of Eq.34 right include two Hsd, so the number of operators becomes twice.
So the conduction electron is more scatterd, to and fro.
Much more scattering patterns have to be considered in this second-order.
(Fig.12) High order = weak interaction ↓ → scattering ↑↑ ?

Strange to say, in these perturbation methods, as higher order interaction is considered, each particle is more scattered.
This interpretation is strange.
Because higher order interactions are much weaker, due to small λ.
So in addition to lack of clear pictures, this method includes self-contradiction.
(Eq.39)

Like Ee.39, anticommutator is used.
c†c is number operator (= f(ε) ).
Summing up all patterns, Eq.38 includes the following equations

In Eq.40, Σ is changed into integration.
As a result, the second order perturbation with respect to Hsd gives the temperature (= T ).
The electric conductivity is
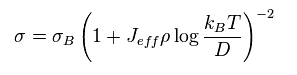
So the electric resistance becomes
(Eq.42)
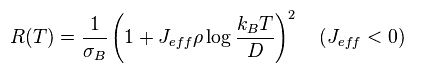
As shown in Eq.42, as the temperature becomes lower, the resistance becomes stronger (= Kondo effect ).
The problem is when the temperature T is equal to 0 (K), this resistance becomes divergent to infinity.
(Eq.43)
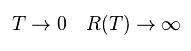
So they try to solve this serious problem using various mathematical tricks such as renormalization.
But as you feel, these unitary definitions of quantum mechanics always cause serious flaws such as infinity.
As you know, the final form of this quantum mechanics is unrealistic 10 dimensional string theory.
Considering all these problems, Bohr model with NO divergence and singularity is more reasonable than strange quantum mechanics.
We can naturally think that de Broglie wave effects by impurities become dominant at very low temperature, which causes resistance to conduction electron.
So Kondo effect can be described by de Broglie waves, in the same way as quantized magnetic flux and ferromegnetism.

2013/9/15 updated. Feel free to link to this site.