(Eq.1)
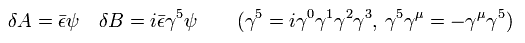
Here we use
(Eq.2)
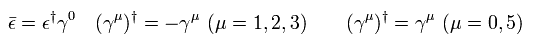
ε means the change of Dirac spinor (× γ0) and ψ means ordinary Dirac spinor.
So in Eq.1, even after transformation, boson terms remain "number" (= transpose spinor × spinor )
Top page (correct Bohr model including the two-electron atoms)
Superstring theory is real ?
Special relativity is wrong ?
To eliminate tachyons from the string theory, it needs supersymmetry.
Supersymmetry means the invariance under supersymmetry transformation.
Here we use the ordinary 4-D Lagrangian and shows some Lagrangians are invariant under supersymmetry transformation.
( Supersymmetric particles have the same mass and different spin (-1/2) with respect to its pair.)
Under the supersymmetric transformation, bosons (= A and B ) change like
(Eq.1)
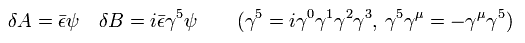
Here we use
(Eq.2)
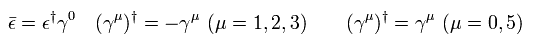
ε means the change of Dirac spinor (× γ0) and ψ means ordinary Dirac spinor.
So in Eq.1, even after transformation, boson terms remain "number" (= transpose spinor × spinor )
And the fermions (= ψ ) change like
(Eq.3)
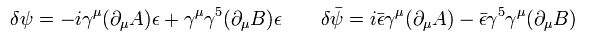
where A means "boson".
Here we consider the Lagrangian of
(Eq.4)

The first term of Eq.4 changes under supersymmetry transformation of Eq.1 as
(Eq.5)

And the second term of Eq.4 changes (using Eq.1) like
(Eq.6)
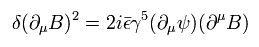
The third term (= fermion ) of Eq.4 changes as
(Eq.7)
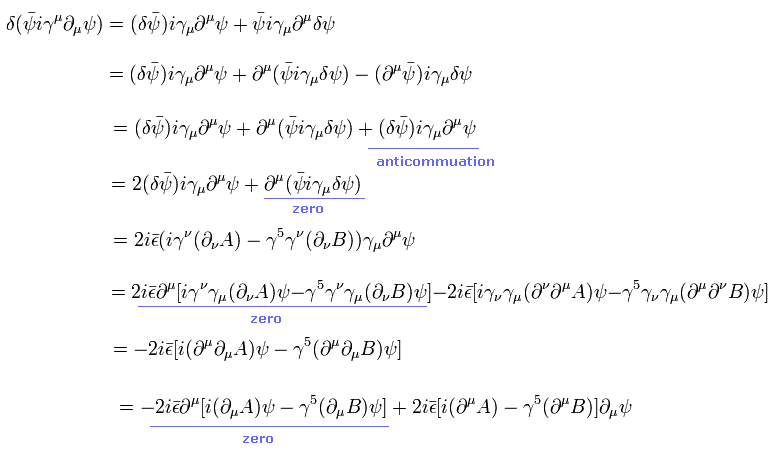
Where we use (+1, -1, -1, -1) version metric tensor.
And by the integral of Lagrangian (= action ), total differential terms become zero.
The sum of Eq.5, Eq.6 and Eq.7 becomes zero.
As a result, Lagrangian of Eq.4 is invariant under supersymmetry transformation.
But as you notice, the transformation form and definitions of Eq.1 and Eq.2 are very "artificial" mathematical things, which are far away from reality.
The string theory has less ultraviolet divergences than the ordinary QED .
But the string theory also uses inifinite harmonic oscillators, which are expressed using exponential functions.
It may cause divergence, when the time variable t is zero.
(Eq.8)
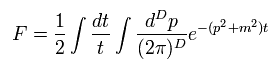
Eq.8 means some probability amplitude after Wick rotation from D-dimension world.
Because the exponential function becomes constant and can not vanish, when t is zero (Eq.8).
Eq.8 case means logarithmic divergence at t → zero after Wick rotation.
For example, 1/t of Eq.8 is gotten by the integral of e-Et with respect to energy variable.
( In this case, to match dimension, this 1/t is used. )
If this divergence is left, various complicated interactions which include gravity become divergent, which are hard to remove.
To avoid the divergence of Eq.8, the string theory introduced the definitions in which F doen't include t=0.
But to use this definition correctly, they had to prove this transformation doesn't cause the change of probability amplitude.
The mass term (=m ) of Eq.8 means internal oscillation of the string.
(Eq.9)
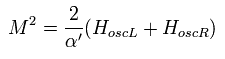
so Eq.8 can be expressed as
(Eq.10)

where we use the formula of
(Eq.11)
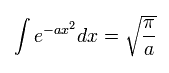
Using Eq.11, Eq.10 becomes
(Eq.12)
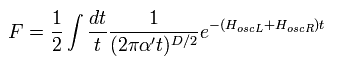
To keep symmetric, Hamiltonians of left-moving and right-moving need to be the same.
So we need to add the factor of
(Eq.13)

As shown in this page, the space variable of the left-moving and right-moving have the opposite signs.
So we can treat s of Eq.13 like space variable of the 2-D string.
Combining Eq.12 and Eq.13, we get
(Eq.14)
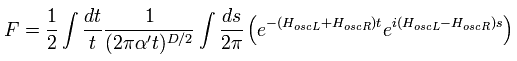
Here we transform the variables like
(Eq.15)
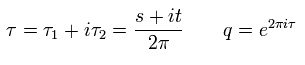
So
(Eq.16)
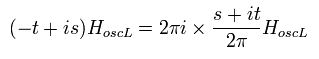
Eq.14 can be expressed as
(Eq.17)
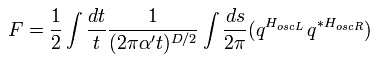
Here we suppose the space variable s is from -π to π and the time t avoids zero, like
(Eq.18)
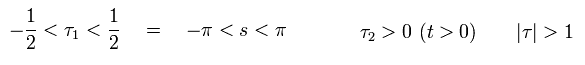
The definition of Eq.18 can eliminate the divergence of Eq.8.
To make the definition of Eq.18 effective, we have to prove the definition of Eq.18 does not influence the overall amplitude.
Here we use the transformation (= Modular transformation ) of
(Eq.19)
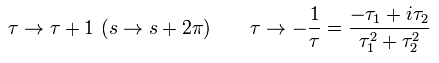
Eq.19 means space variable "s" is periodic at the interval of 2π.
And the probability amplitude does not change under the scale transformation of the two variables and the flip of "s".
Because, when we define the 2-D "strange" string, these two variables must be arbitrary.
From Eq.76 and Eq.84 of this page, boson Hamiltonian is expressed as
(Eq.20)

Of course, they use strange concept of "zeta" function here.
Boson's number can be arbitrary ( "n" is from 0 to ∞ ).
So its exponential function is
(Eq.21)
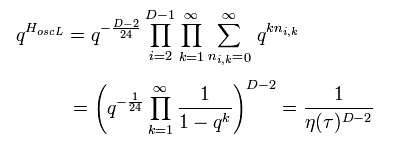
where we sum the geometric series of qk.
And here, Dedekind eta function is defined as
(Eq.22)
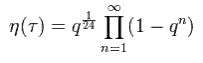
From Eq.15, Eq.21, Eq.17 can be expressed as
(Eq.23)

where we use
(Eq.24)
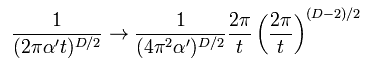
Under the Modular transformation of Eq.19,
(Eq.25)
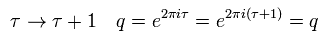
So the amplitude of Eq.23 does not change.
And Dedekind eta function is known to change like
(Eq.26)
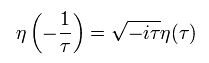
And from Eq.19
(Eq.27)
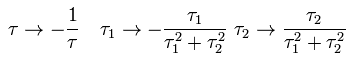
and from Eq.15,
(Eq.28)
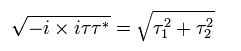
From Eq.26, Eq.27 and Eq.28, the amplitude Eq.23 does not change under the Modular transformation of Eq.27 (Eq.19).
(Eq.29)
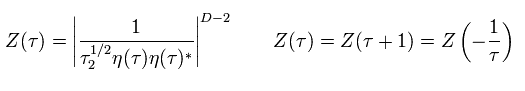
From Eq.15, the remaining part of Eq.23 does not change.
To erase "tachyon", we have to define "artificially" like
(Eq.30)
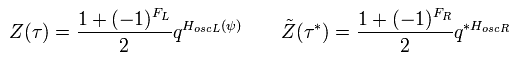
Eq.30 is called GSO projection.
(-1)FL means when H includes "odd" number of NS sector string, it besomes "minus".
So under the unitary transformation of Eq.30, it leaves only the cases where even-number NS strings are included in each left or right-moving string.
"NS-sector" means antiperiodic boundary and "R-sector" means periodic boundary conditions.
( Caution: "R" of R-sector is different from "R" of the right-moving string. )
So the amplitude including bosons and fermions becomes ( when D=10 )
(Eq.31)

Boson part is invariant under Modular transformation, as shown above.
So we need to prove fermion's part is also invariant.
From Eq.99 of this page, NS-sector fermion's part is
(Eq.32)

where we remove boson's vacuum.
First, we consider "1" part (= without (-1)FL ) of Eq.30
NS sector without GSO projection is
(Eq.33)

Different from boson (= number "n" is from 0 to ∞), fermion's number n is "0" or "1" due to anticommutation relation (= Pauli exclusion principle ).
Here elliptic theta functions are defined as
(Eq.34)
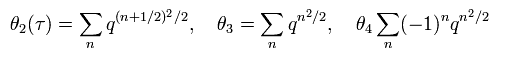
And "R" sector Hamiltonian is
(Eq.35)
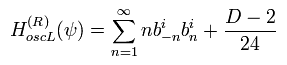
where
(Eq.36)
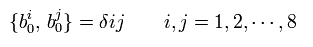
"R"-sector fermions satisfy anticommutation relation, but its angular frequency is an integer like bosons.
( This is only a definition, so we have to obey this rule. )
Different from NS-sector, "R"-sector fermions include "defeneracy" of zero angular frequency (= zero energy ).
8 (= 10-2 ) oscillators form four pairs of creation and annihilation operators, which can commute with R-sector Hamiltonian.
(Eq.37)
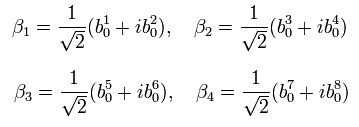
(Eq.38)
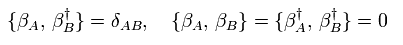
Four kinds of creation operators mean R-sector ground state includes 24 = 16 kinds of states (= each zero-energy particle exists or not ).
As a result, from Eq.35, R-sector amplitude (D=10) becomes
(Eq.39)
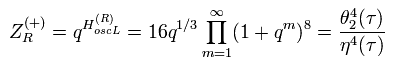
where n → m, and fermion's number is "0" or "1".
Next we consider the case in which (-1)FL operator of Eq.30 acts on the amplitude.
When NS-sector fermion's number is "1", it becomes "minus", so Eq.33 becomes
(Eq.40)

And "R"-sector fermion is supposed to be zero, when (-1)FL acts on it, because, (-1)FL acts only on NS-sector.
(Eq.41)
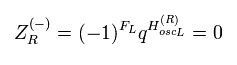
Here we suppose that under (-1)FL, NS-sector vacuum becomes "minus" like
(Eq.42)
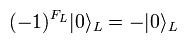
Eq.42 means NS-sector vacuum is eliminated under GSO projection of Eq.30.
So considering all cases under GSO projection, the partition function of fermions becomes
(Eq.43)
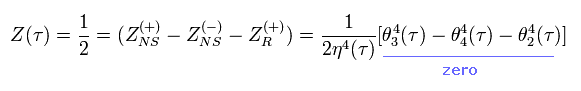
In Eq.43, due to the phase difference, R-sector is the opposite sign.
And due to Eq.42, NS sector under GSO projection also becomes minus.
( This is a little difficult to imagine. )
According to the formula of elliptic theta function, the last term of Eq.43 is always zero, which means fermion's case is also Modular-invariant.
This case is valid only in D=10 dimensions.
And as shown in Eq.42, NS-sector vacuum is eliminated under the GSO transfomation of Eq.30.
And the vacuum of the same number R-sector fermion with the same mass (= Eq.35 ) can cancel out the boson's vacuum, because they are just opposite signs.
And of course, NS and R sector strings have the same number, as shown in Eq.43.
This means "supersymmetric particles" with the same mass eliminates tachyon's vacuum.
( Do you understand this very abstract reason ? )
Unfortunately, there are NO clear images and reality here.
It seems that the present string theory is "wandering" around inside only "mathematical" and unimaginable world, I think.
How do you think about it ?
The dimentions "10" is also gotten from gauge fixing and the removal of anomaly of the central charge caused by fixing.
The most important point is whether these "mathematical" concepts are linked to this real world or NOT.

2012/7/18 updated. Feel free to link to this site.