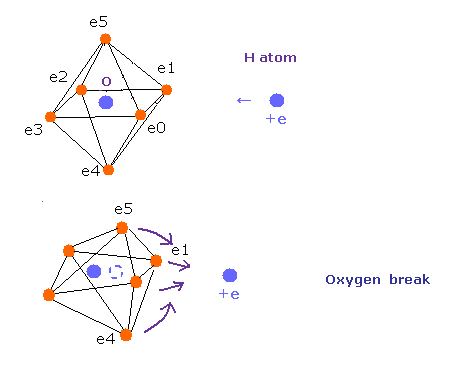
Top page (correct Bohr model including the two-electron atoms).
Strange "Spin" is NOT a real thing.
Special relativity is wrong.
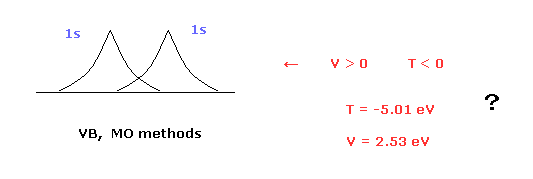
(Fig.1) Molecular orbital methods violates Virial theorem.

Valence bond ( VB ) and molecular orbital ( MO ) methods are famous as
quantum mechanical approches to hydrogen molecule (H2).
In these quantum mechanical methods, two 1s hydrogen atom's wavefunctions are used in H2 molecule. ( See this page. )
( H2 bond energies, VB = 3.14 eV, MO = 2.68 eV, are different from experimental values (= 4.74 eV ). )
The problem is these methods disobey Virial theorem.
Because, these quantum mechanical H2 molecules have negative kinetic energy (= T ) and positive potential energy (= V ).
This problem has been known since 1960s.
(Fig.2) Quantum mechanical helium atom ?
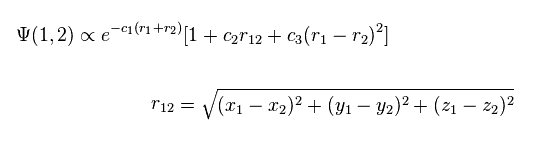
As shown in this page, quantum mechanical variational methods cannot give exact energy values, when the system contains two electrons.
In this case, they try to use the variational wavefunctions including variables of interelectron distance (= r12, Fig.2 ).
For example, in Fig.2, as the two electrons of helium come close to each other, the wavefunction amplitude becomes smaller.
This is one of artificial manipulations.
(Fig.3) Manipulation of interelectron distance.
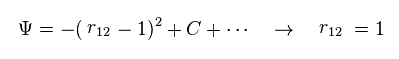
In Fig.3, when the interelectron distance r12 becomes shorter than "1", wavefunction amplitude becomes smaller.
So we can choose the state of r12 = 1, artificially.
Quantum mechanical helium and hydrogen molecule (H2) completely depend on these tricks..
And these models clearly indicates two electron of helium and H2 are actually moving around to avoid another electron.
First, we review H2 molecular model based on Bohr's orbit.
If you have not read this page, see that page first.
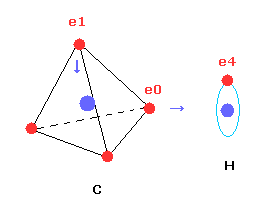
(Fig.4) Estimated H2 molecule.
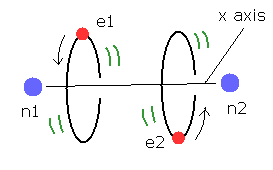
Considering the internuclear distance ( 0.7414 × 10-10 m ) and Coulomb relations among two electrons and nuclei, it is natural that we think the actual electron's states of H2 molecule is like Fig.4.
Of course, Coulomb relations are most important concept also in quantum chemistry.
And another important concept which determines molecule's configuration is de Broglie wavelength.
Fig.4 is an "average" orbit to apply Virial theorm.
Considering interference of two de Broglie wave, actual H2 configuration becomes this.
(Fig.5) If de Broglie wavelength doesn't exist ?
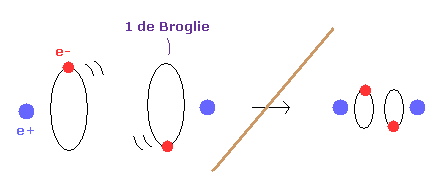
If the concept of de Broglie wavelength doesn't exist, the electron's orbital radius of hydrogen atom can be smaller to zero.
As a result, internuclear distance of H2 molecule can be shorter as it likes, because the repulsive force between two nuclei can be cancelled out by arbitrary small electron's orbit.
So due to the concept of de Broglie wavelength, the internuclear distance ( 0.7414 × 10-10 m ) of H2 is kept.
(Fig.6) Both nuclei and electrons need to be stable in H2.
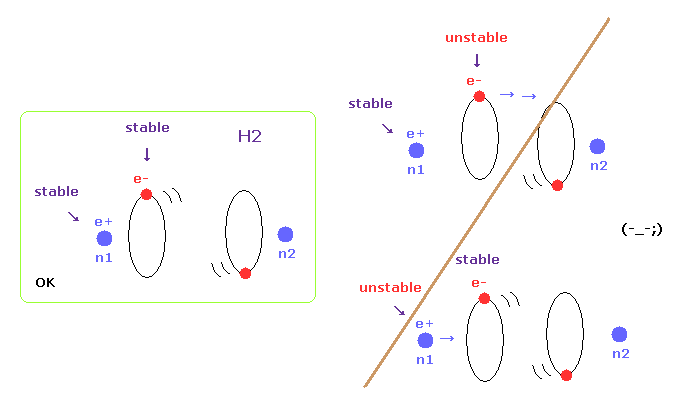
When molecules are stable at some nuclear distance, both of their nuclei and electron's orbits need to be stable.
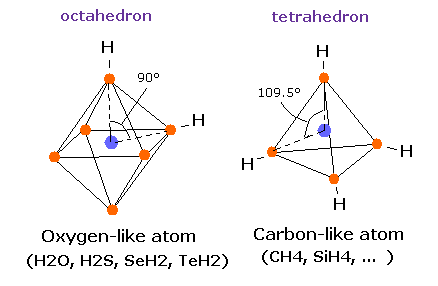
In this page, we show various molecules such as H2, CH4, and H2O have unstable electrons ( or nuclei ), when their internuclear distances are not experimental values.
(Fig.7) H2 molecule.
Here we calculate the number of de Broglie wave in one orbit using Fig.7 model and following programs.
Sample JAVA program of H2 molecule.
C language program of H2 molecule.
Here we use the new unit of 1 MM = 1 × 10-14 meter.
In this program, first we input the internuclear distance (= nuc in MM ) of H2.
And then input y-coordinate "r" (in MM) , and x-coordinate "a" ( in MM ) of electron 1.
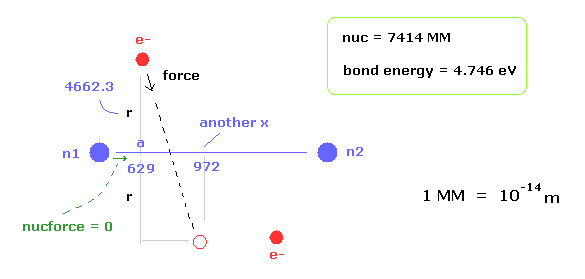
(Fig.8) Various forces at ( a, r ).
From the inputted values, this program outputs the total force acting on nucleus 1 (= nucforce ), and ( x, y ) components of forces acting on electron 1 (= elefx, elefy ) at the position of ( a, r ).
These forces are expressed as the ratio to the force between electron and nucleus of H atom's ground state.
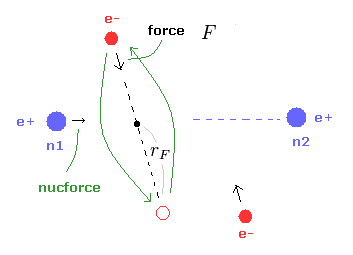
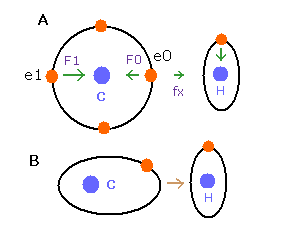
(Fig.9) Force F acting on e1.
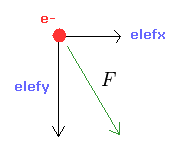
From the inputed values ( a, r, nuc ), we calculate the total potential energy V.
Using Virial theorem, we can get the total energy E = 1/2 V and kinetic energy T = -1/2 V.
From this kinetic energy, we obtain the electron's velocity (= v ) and de Broglie wavelength (= h/mv ).
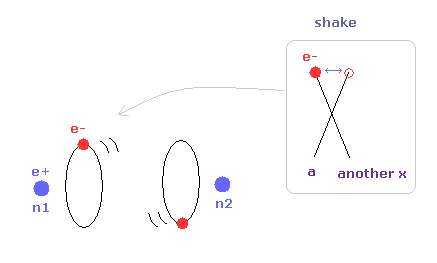
(Eq.1) F = centrifugal force.
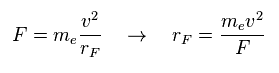
Here we suppose the force F is some centrifugal force.
From the relation of Eq.1, we can get the rotation radius (= rF ).
(Eq.2) de Broglie wave in one orbit.
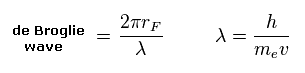
Using the de Broglie relation ( λ = h/mv ), we caluclate the number of de Broglie waves included in one orbit (= 2πrF ).
Using Virial theorem, we can get the binding energy of H2 atom at the position of ( a, r ).
(Fig.10) Another x coordinate of electron.
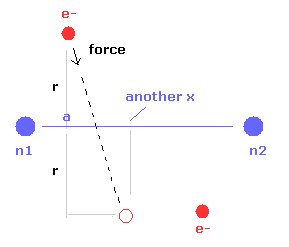
And this probram also outputs another x coordinate (in MM) of electron 1 in the direction of the force F, as shown in Fig.10.
This x coordinate becomes a indicator of the electron's shaking in the x direction.
Furthermore, we compute de Broglie waves and the force acting on electrons at another x positions.
And we get average binding energy and de Broglie waves in one orbit (= Table 1).
Because electron's orbit is shaking transversely, so we need to consider their average effect.
First we think about the case when the binding energy (= 4.746 eV ) and the internuclear distance (= 0.7414 × 10-10m = 7414 MM ) are experimental values.
(Eq.3) Experimental values of H2.
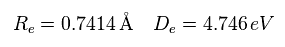
When the electron 1 is ( a = 629 MM, and r = 4662 MM ), the total forces acting on nucleus become zero.
( nucforce = 0. At this point, two nuclei are stable. )
(Fig.11) Experimental values.
At this point, de Broglie waves included in one orbit (= Eq.2) becomes 0.977.
This value is almost 1, but is a little different.
Because the electron's orbit is shaking in the x direction.
At the another x coodinate ( a, r ) = ( 972, 4662 ), this de Broglie wave becomes 1.009.
As a result, the average de Broglie waves become ( 0.977 + 1.009 ) / 2 = 0.993.
This value is closer to "1".
| nuc (MM) | r (MM) | a (MM) | Energy (eV) | another x | nucforce | aver waves | elefx | after elefx |
|---|---|---|---|---|---|---|---|---|
| 6000 | 4875.1 | 1662 | 3.699 | 1858 | 0.00 | 0.9933 | +0.024 | +0.013 |
| 6500 | 4744.3 | 1059 | 4.408 | 1351 | 0.00 | 0.9933 | +0.039 | +0.005 |
| 7000 | 4684 | 775 | 4.689 | 1107 | 0.00 | 0.9933 | +0.046 | -0.006 |
| 7200 | 4671 | 697 | 4.732 | 1037 | 0.00 | 0.9933 | +0.047 | -0.011 |
| 7414 | 4662.3 | 629 | 4.746 | 972 | 0.00 | 0.9933 | +0.048 | -0.014 |
| 7600 | 4658 | 577 | 4.738 | 922 | 0.00 | 0.9933 | +0.048 | -0.017 |
| 8000 | 4657 | 488 | 4.671 | 831 | 0.00 | 0.9933 | +0.048 | -0.023 |
Here, new unit 1 MM = 1 × 10-14 meter.
As shown in Table 1, when we choose the common conditions of nucforce = 0 and average de Broglie wave = 0.9933, the binding energy at internuclear distance of nuc = 7414 MM (= experimental value ) becomes the largest.
So as I said, when we consider the stable nuclei and de Broglie wavelength, the most stable hydrogen configuration is determined.
| nuc (MM) | r (MM) | a (MM) | Energy (eV) | elefx | elefy | nucforce | waves |
|---|---|---|---|---|---|---|---|
| 7414 | 4665 | 890 | 4.746 | 0.00 | 1.271 | 0.08 | 1.001 |
When the x component of force acting on electron is zero ( elefx = 0.00 ), de Broglie wave becomes just 1.001.
This a (= x ) position is between 629 and 972 of Table 1.
(Fig.12) Two H atoms are completely dissociated.
Next we think about the reason why H2 molecule becomes most stable when the internuclear distance of H2 is nuc = 7414 MM (= experimental value ).
In Fig.12, two hydrogen atoms are completely dissociated, so the binding energy is just zero.
(Fig.13) Most stable H2 configuration.
As the two nuclei come closer to each other, each electron can interact with two positive nuclei.
So, the bond energy becomes bigger, which means stable H2 molecule is formed.
(Fig.14) Repulsive force of two electrons.
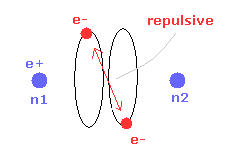
But when the two nuclei come closer to each other than the experimental value of 7414 MM, the repulsive force between two electrons are stronger.
As a result, "effective" central positive charge in is smaller.
So under the common de Broglie wave's condition, this bond energy is smaller than the experimental value. ( See Table 1. )
(Fig.15) When internuclear distance becomes shorter.
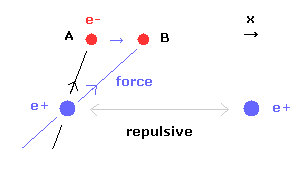
When the internuclear distance becomes shorter, the repulsive force between nuclei becomes stronger.
To cancel this repulsive force out, the two electrons need to move in the direction of the center.
As shown in Fig.15, as the electron 1 moves in the x direction ( A → B ), atrractive force of electron 1 becomes stronger in the x direction.
But in this case, the repulsive force between two electrons becomes stronger in Fig.14.
(Fig.16) Internuclear distance becomes shorter → unstable electron.
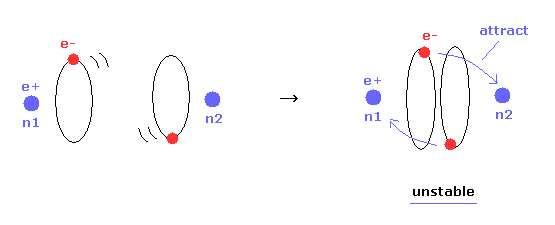
In Table 1, we choose the condition of nuclear stability ( nucforce = 0 ).
Of course, when the molecular configuration is stable, both nuclei and elecgtrons need to be stable.
As shown in Table 1, as the internuclear distance becomes shorter than experimental value (= 7414 MM ), electron's orbit becomes unstable.
Because the forces acting on electrons at the positions of "a" and "another-x" are always positive ( elefx > 0, after-elefx > 0 ).
( So this unstable electron's orbit is always attracted to another nucleus n2. See Fig.17 right. )
If the electron's orbit is stable around some place, the electron needs to make U-turn.
In this case, elefx is positive and after-elefx needs to be negative. ( See Fig.17 left. )
(Fig.17) Internuclear distance becomes shorter → unstable electron.
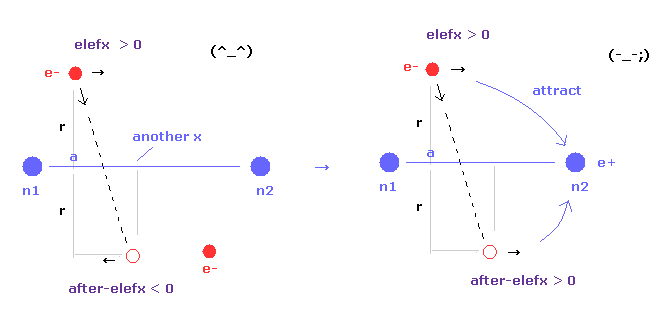
As internuclear distance becomes shorter, electron's x coordinate "a" becomes larger to make nuclei stable.
So, the influence by n1 nucleus to electron 1 is weaker, and n2 influence is stronger.
As a result, electron's orbits tend to be attracted to another nucleus, and be unstable.
This electron's unstability is one of the main reasons why internuclear distance of 0.7414 × 10-10 m (= experimental value ) is most stable.
(Fig.18) Stable orbit is shaking and make U-turn.
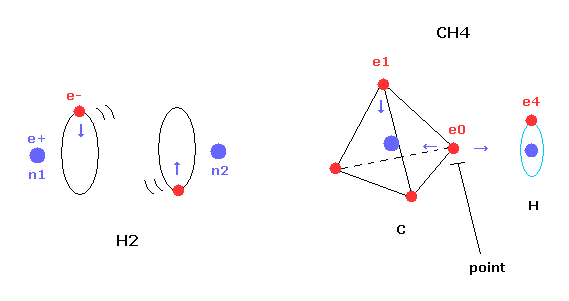
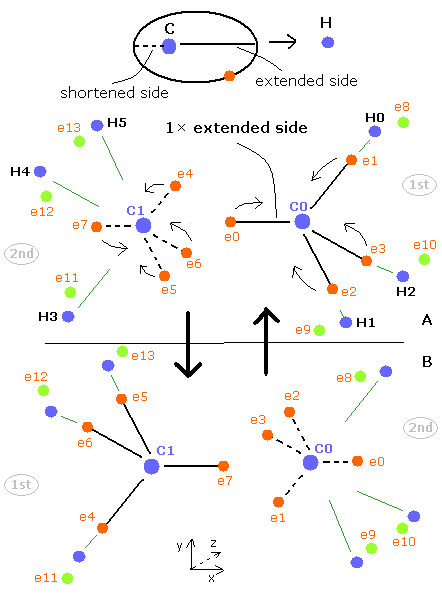
Next we investigate the true nature of methane (CH4) using Bohr's orbit.
(Fig.19) Transverse projecting point of CH4.
We succeeded in expressing hydrogen molecule (H2) using Bohr's orbit correctly, in the above section.
And we show the binding energy of H2 is maximum, when the internuclear distance is experimental value (= 7414 MM ).
Here we use new unit 1 MM = 1 × 10-14 meter.
But different from simple hydrogen molecule, carbon atom of methane (CH4) contains four tetrahedrally distributed valence electrons.
So even if we try to arrange one electron of carbon parallel to the hydrogen's orbit, another of four electrons always protrudes toward hydrogen atom.
This projecting electron of carbon strongly attracts the hydrogen nucleus and lowers the potential energy.
And as I say later, this projecting electron is the key player to determine the instability.
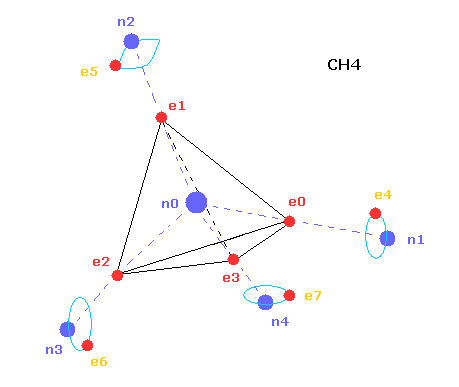
(Fig.20) Structure of CH4 in computing program.
Here we use the JAVA program below to investigate CH4 true nature.
Methane molecule (CH4) JAVA program.
In the above computing program, we use the Fig.20 methane model.
Four valence electrons ( e0, e1, e2, e3 ) of carbon atom are arranged tetrahedrally.
And four hydrogen atomic nuclei also are distrubuted tetrahedrally.
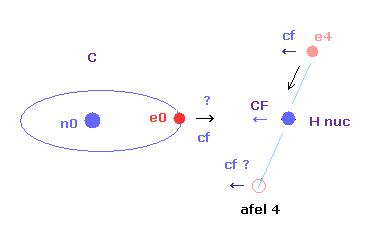
As shown in Fig.20, electron e0 of carbon and n1 nucleus of hydrogen are on the same line.
( In the same way, e1-n2, e2-n3, e3-n4 are on each common line. )
(Fig.21) Cross section of CH4 (= x-z plane ).
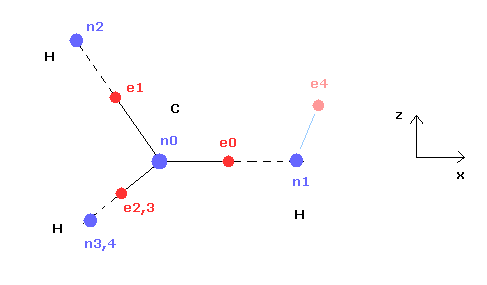
Fig.21 is the cross-sectional view ( x- z plane ) of Fig.20.
In the above program, we can change only the coordinate of electrons e0 and e4 in the textboxes.
( Only x coordinate of e0 and x, z coordinates of e4 can be manipulated. )
Based on the inputted coordinates of e0 and e4 in the textboxes, the remaining carbon electrons ( e1-e3 ) and hydrogen electrons ( e5-e7 ) are automatically arranged tetrahedrally.
So x coordinates of electrons 1, 2, 3 ( and H nuclei n2, 3, 4 ) are always the same.
( This program only shows each value, and not pictures due to the limit of screen, sorry. )
(Fig.22) Screen just after running program.
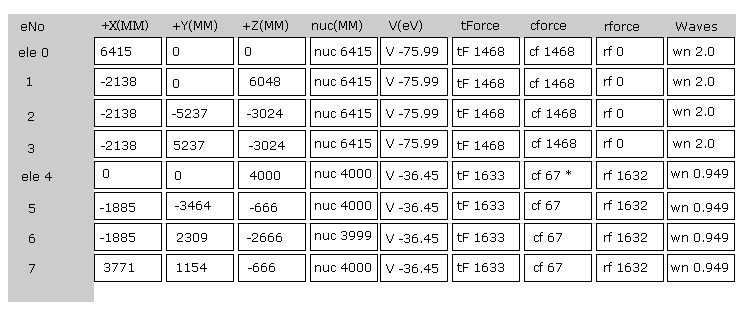
Fig.22 is the upper part, which appears on the screen just after you run the JAVA program.
ele 0, 1, 2, 3 are the electrons which belong to carbon atom.
+X(MM), +Y(MM), +Z(MM) are relative coordinates with respect to the nucleus, to which each electron belongs to.
( ele 0-3 belong to carbon nucleus n0, and ele4 belongs to H nucleus n1, ele5 is n2, ele6 is n3, and ele7 is n4. )
"nuc" means the distance between each electron and nucleus, to which the electron belongs to.
Here new unit 1 MM = 1 × 10-14 meter is used.
"V(eV)" is potential energy of each electron.
"tForce" is total force, which acts on each electron.
"cforce" is the force component acting on each electron in the direction to the center (= C nucleus ).
"rforce" is the force component acting on each electron ( e4-e7 ) toward each C nuc - H nuc line.
"Waves" is de Broglie waves contained in one orbit of each electron.
(Fig.23) Force = 1000.
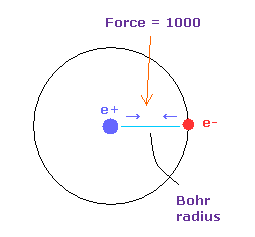
In Fig.22, the force between electron and nucleus in H atom ground state is supposed to be "1000".
So when the distance between electron and +e nucleus is Bohr radius, its force becomes 1000.
For example the force of 1468 is 1.468 times that in H atom ground state.
We calculate each de Broglie wavelength from each kinetic energy (T).
Here Virial theorem ( -1/2V = T ) is used.
( "V" is potential energy. )
In cases of atoms (= single nucleus ) and H2 molecule, their calculations are simple.
But when a molecule contains two nuclei and asymmetric multi-electrons, we need to take care a little.
From each kinetic energy, we can get the electron's velocity (= v ) and de Broglie wavelength (= h/mv ).
(Eq.4) Total force F = centrifugal force.
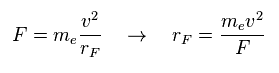
Here we suppose total forces F of them are some centrifugal forces like hydrogen molecule case above.
From the relation of Eq.4, we can get ( approximate ) rotation radius (= rF ).
(Eq.5) de Broglie wave in one orbit.
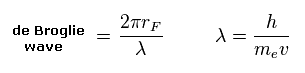
Using the de Broglie relation ( λ = h/mv ), we caluclate the number of de Broglie waves included in one orbit (= 2πrF ).
Carbon outer electrons e0-e3 should be "2", and hydrogen's electrons e4-e7 should be "1" in de Broglie waves.
(Fig.24) C-H bond of methane.
Breaking all four C-H bonds of methane requires 1663 kJ/mol ( = 17.235 eV ).
So the ground state energy of methane (4 carbon's valence electrons + 4 hydrogen atoms) becomes -148.024 -54.416 -17.235 = -219.675 eV.
(Here, the total energy of the four valence electrons of carbon is supposed to be -148.024 eV = sum of 1-4 ionization energies.)
And the average bond length of C-H bond is 1.09 × 10-10 meter (=10900 MM).
(Fig.25) de Broglie waves of C-H bond
In the e0 electron Fig.25A, we cannot use the upper calculating method of de Broglie's waves as it is.
In the electron 0 (e0) of carbon (C), due to the opposite attractive force (fx) from the hydrogen nucleus, force F0 becomes weaker than force F1 of electron 1, as shown in Fig.25A.
So, in Eq.4, "temporary" radius r1 of e0 becomes longer than e1.
This means more de Broglie's waves (> 2.0) are contained in e0 orbit than e1 ( < 2.0 ), when we use the above calculating methods directly.
But if we pay attention to only one electron's orbit (Fig. 25B), the number of de Broglie's waves ( = 2.0 ) is kept by changing the position and shape of its orbit.
( A positive H nucleus translates this electron's orbit a little, and make it "elliptical". )
So when we calculate C-H carbon electron's wave in one orbit, we condsider the forces and energies only inside carbon atom, approximately.
(Fig.26) Each force in C-H bond
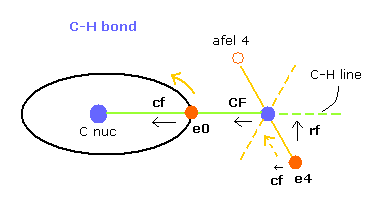
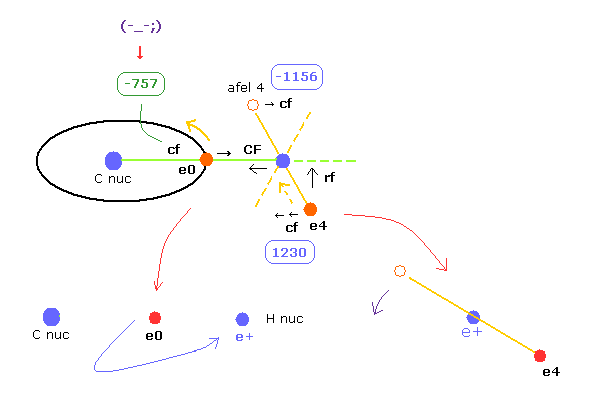
In this program, "cf" means the force component acting on each electron toward C nucleus.
And "rf" means force acting on electron 4-7 toward ( perpendicular to ) each C-H line.
"afel 4" means the electron's position after moving it in the direction of force.
This afel 4 corresponds to "another x" of Fig.10.
( So each electron is oscillating transversely around this place. )
For the electron's orbit to be stable at some point, this "cf" of e4 is positive, and "cf" of afel 4 is negative.
And their absolute values need to be almost the same to be stable.
( This is one of important points in stable molecular bonds. )
"CF" means force acting on each H nucleus toward C nucleus.
So when these CF and cf are positive values, these particles are attracted toward central C nucleus.
(Fig.27) "afel 4" position.
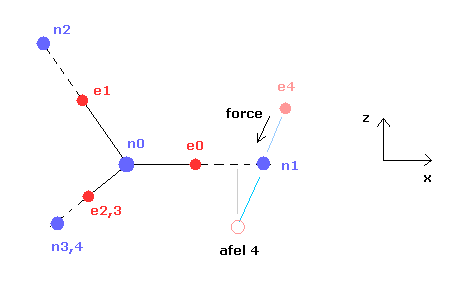
When calculating "afel 4" x coordinate, we use the force component ratio of "cf" to "rf".
And z (and y ) coordinate of afel 4 is supposed to be equal to the original e4.
(Fig.28) Average positions ?

When we try to calculate de Broglie waves and forces of each particle using Fig.28 distribution, four outer electrons and hydrogen nuclei are attracted to each other more than the average values.
Carbon outer electron's orbit radius is about 6400 MM, which is almost same as Bohr radius 5292 MM of hydrogen atom.
But carbon outer electron's orbit is two de Broglie wavelength, which means their velocity is almost twice faster than that of H atom electron.
So we need to consider average distribution about carbon atom, when we consider the interaction with H atom.
(Fig.29) Average positions of outer electrons of carbon.
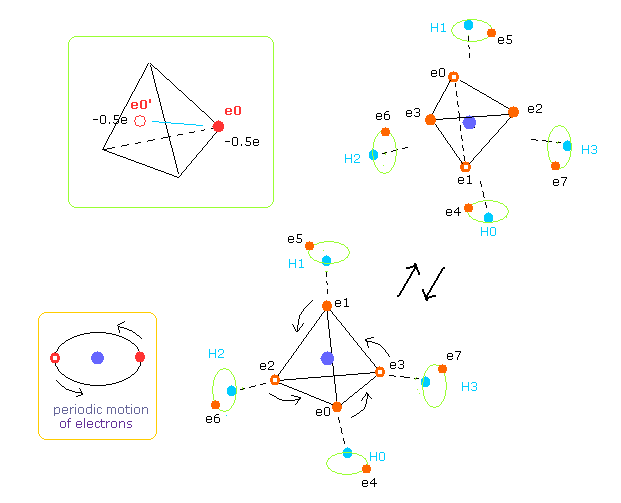
As shown in Fig.29, four outer electrons of carbon are moving on almost elliptical orbits.
So the opposite positions of each electron is important to take average values, too.
Actually Virial theorem is valid, when their motions are equal to average ones during infinite time period.
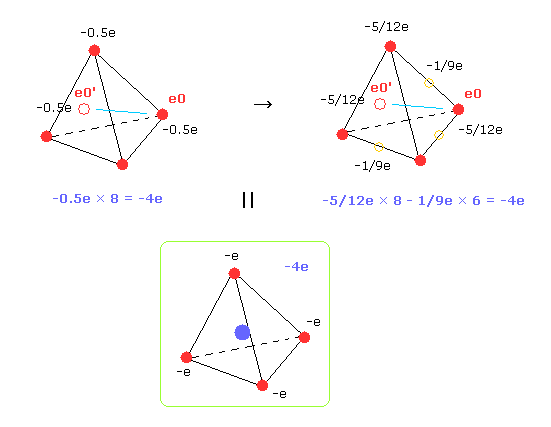
So carbon's four outer electrons moving faster can be considered as eight electrons with half charge.( -1.0e → -0.5e, -0.5e × 8 = -4e. ).
And that pair electron with half charge are supposed to be just at the opposite positions across C nucleus.
( Of course, when we compute repulsive potentials among electrons 0-3 themselves, the original four valence electrons need to be used. )
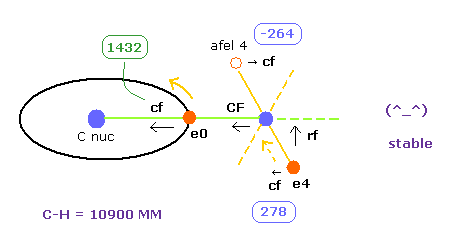
Here we show the result, when we choose experimental value (= 10900 MM ) of C-H bond length.
Please input the coordinates ( values of "←" in ele 0 and ele 4 ) below into each textbox and push "enter" key after running program.
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| ele 0 | 6415 ← | 0 | 0 | nuc 6415 | V -76.45 | cf 1432 | rf 0 | wn 2.0 |
| ele 4 | 520 ← | 0 | 4060 ← | nuc 4093 | V -35.03 | cf 278 | rf 1568 | wn 0.917 |
| afel 0 | 6415 | 0 | 0 | nuc 6415 | V -75.17 | cf 1488 | rf 0 | wn 2.0 |
| afel 4 | -922 | 0 | 4060 | nuc 4163 | V -36.28 | cf -264 | rf 1396 | wn 1.083 |
| H0 nuc | total V | averwave-0 | averwave-4 |
|---|---|---|---|
| force= 0 | -445.95 eV | wave 2.0 | wave 1.0 |
Table 1 shows the results when C-H bond length is experimental values (= 10900 MM ).
The average de Broglie waves are "2.0" in electron 0, and "1.0" in electron 4.
And we stop H0 nucleus ( force CF = 0, see Fig.26 ).
Under this condition, total potential energy is -445.95 eV, which is almost same as experimental values of -219.675 × 2 = -439.35 eV.
( This little difference is caused by the difference in electron's distribution, as is explained later. )
Important point is that electron 4's orbit is also stable when C-H length is 10900 MM.
Becase transverse force acting on ele4 ( cf = 278 ) is just opposite to that of afel 4 ( cf = -264 ).
(Fig.30) Both electon and nucleus are stable in methane.
This electron's stability is similar to hydrogen molecule (H2) of Fig.16, Fig.17 and Fig.18. ( See also Table 1. )
Also in hydrogne molecule, the sign of after-elefx is opposite to elefx, and electron is stably shaking around some place.
(Fig.17) Stable electron's orbit of H2 molecule = left figure.

(Fig.18) Stable orbit is shaking and makes U-turn.

Next we choose C-H bond length = 9500 MM (= 0.950 × 10-10 meter ), and click C-H button.
And then we adjust ele 0 and ele 4's coordinates, aiming at CF=0 ( nucleus stability ), average de Broglie waves 2.0 (ele0) and 1.0 (ele4).
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| ele 0 | 6415 | 0 | 0 | nuc 6415 | V -79.06 | cf 232 | rf 0 | wn 2.0 |
| ele 4 | 927 | 0 | 3129 | nuc 3263 | V -44.05 | cf 782 | rf 2341 | wn 0.834 |
| afel 0 | 6415 | 0 | 0 | nuc 6415 | V -76.33 | cf 353 | rf 0 | wn 2.0 |
| afel 4 | -1165 | 0 | 3129 | nuc 3338 | V -46.45 | cf -715 | rf 1771 | wn 1.167 |
| H0 nuc | total V | averwave-0 | averwave-4 |
|---|---|---|---|
| force= 0 | -492.47 eV | wave 2.0 | wave 1.0 |
(Fig.31) "e4" is attracted to C, and "e0" is attracted to H.
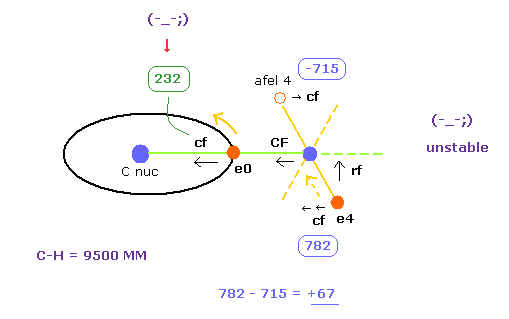
As shown in Table 4, when C-H bond length is a little shorter (= 9500 MM ) than the experimental value (= 10900 MM ), electron's stability is broken.
First, electron 0, which belongs to carbon nucleus, comes to be attracted to H nucleus too much.
Becuase "cf" of e0 is much smaller (= 232 ) than the Table 3 (= 1432 ).
(Fig.23) Force = 1000.

As I said in Fig.23, we define the force between electron and nucleus in H atom ground state is "1000".
So when the distance between electron and +e nucleus is Bohr radius, its force becomes 1000.
The central force "232" is too small for carbon's electron to move around carbon nucleus stably.
(Fig.31') If hydrogen becomes too close to carbon, methane is unstable
Second, C-H bond length is shorter, H nucleus is more attracted to electron 0 of carbon atom.
To cancel this attractring force, electron 4 of H atom needs to be shaking more widely in the transverse direction (= Fig.31'A ).
But on the other hand, carbon nuclear attracting force against electron 4 becomes stronger (= Fig.31'B ).
So it is unnatural that H electron's orbit leans more transversely like Fig.31'A, when the carbon attractive force becomes stronger.
Because electron4's orbit cannot keep such stable motion and position to stop H nucleus.
( "cf" difference +67 of Table 4 (Fig.31) is bigger than +14 of Table 3 )
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| ele 0 | 6415 | 0 | 0 | nuc 6415 | V -80.89 | cf -757 | rf 0 | wn 2.0 |
| ele 4 | 1064 | 0 | 2676 | nuc 2879 | V -50.13 | cf 1230 | rf 2892 | wn 0.795 |
| afel 0 | 6415 | 0 | 0 | nuc 6415 | V -77.11 | cf 588 | rf 0 | wn 2.0 |
| afel 4 | -1212 | 0 | 2676 | nuc 2937 | V -52.95 | cf -1156 | rf 1934 | wn 1.204 |
| H0 nuc | total V | averwave-0 | averwave-4 |
|---|---|---|---|
| force= 0 | -524.11 eV | wave 2.0 | wave 1.0 |
(Fig.32) e0 is attracted to H, and e4's orbit leans transversely.
When the C-H bond length is much shorter (= 9000 MM ), electron 0 of carbon is attracted to H nucleus instead of C nucleus.
So the carbon structure is broken.
And e4's orbit leans too much transversely, which makes e4's motion unstable.
The "cf" difference 1230 - 1156 = 74 is wider than above.
(Fig.32') If C-H length becomes shoter.
As a result, when C-H bond length is shorter than the experimental value, one of electron's or nuclear motions become unstable.
So we need to think about both stablities of electron and nucleus in molecular bonds.
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| ele 0 | 6415 | 0 | 0 | nuc 6415 | V -75.47 | cf 1797 | rf 0 | wn 2.0 |
| ele 4 | 273 | 0 | 4494 | nuc 4502 | V -31.91 | cf 141 | rf 1320 | wn 0.956 |
| afel 0 | 6415 | 0 | 0 | nuc 6415 | V -74.77 | cf 1829 | rf 0 | wn 2.0 |
| afel 4 | -690 | 0 | 4494 | nuc 4546 | V -32.6 | cf -142 | rf 1248 | wn 1.044 |
| H0 nuc | total V | averwave-0 | averwave-4 |
|---|---|---|---|
| force= 0 | -429.59 eV | wave 2.0 | wave 1.0 |
When C-H bond length is longer than experimental values, the potential energy becomes higher.
( Compare -445.95 eV of Table 3 and 429.59 eV of Table 6. )
So the equilibrium point of bond energy and stability determines the methane (CH4) configuration.
Of course, in this process, two main properties of Coulomb force and de Broglie waves ( 2.0 and 1.0 ) play crucial roles.
(Fig.33) If carbon's four outer electrons are more widely distributed.
In the upper section, to get the average H atom orbit and values, we consider four outer electrons of carbon are distribited around C nucleus as 8 electrons with half charge.
Actually, carbon's outer electrons are moving faster than hydrogen's electron.
And even after one of 4 carbon's electrons leaves, another electron soon comes close to hydrogen.
Their rotating periods are different.
But as shown in Table 3, computing result (= -445.95 eV ) of total potential energy is a little different from the experimental value (= -439.35 eV ).
So we suppose carbon's four electrons are more widely distributed around C nucleus.
In Fig.33 right, we suppose 8 electrons with charge -5/12e and six electrons ( on six sides of tetrahedron ) with -1/9e.
Of course, total charges remain to be -4e.
Methane molecule (CH4) JAVA program-2.
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| ele 0 | 6415 | 0 | 0 | nuc 6415 | V -76.02 | cf 1403 | rf 0 | wn 2.0 |
| ele 4 | 405 | 0 | 4308 | nuc 4326 | V -33.07 | cf 219 | rf 1427 | wn 0.928 |
| afel 0 | 6415 | 0 | 0 | nuc 6415 | V -74.91 | cf 1431 | rf 0 | wn 2.0 |
| afel 4 | -918 | 0 | 4308 | nuc 4404 | V -34.2 | cf -199 | rf 1299 | wn 1.072 |
| H0 nuc | total V | averwave-0 | averwave-4 |
|---|---|---|---|
| force= 0 | -436.41 eV | wave 2.0 | wave 1.0 |
This CH4 electron's distribution shows almost experimental value (= -439.35 eV ).
And like Table 3, cf of ele4 and afel 4 are proper values ( 219 and -199. )
These values are opposite in the sign, and their absolute values are almost same ( 219 - 199 = 20. )
This means electron 4's orbit is stable in this model.
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| ele 0 | 6415 | 0 | 0 | nuc 6415 | V -78.22 | cf 158 | rf 0 | wn 2.0 |
| ele 4 | 864 | 0 | 3415 | nuc 3522 | V -40.6 | cf 633 | rf 2064 | wn 0.844 |
| afel 0 | 6415 | 0 | 0 | nuc 6415 | V -75.84 | cf 1431 | rf 0 | wn 2.0 |
| afel 4 | -1232 | 0 | 3415 | nuc 3630 | V -43.08 | cf -499 | rf 1649 | wn 1.156 |
| H0 nuc | total V | averwave-0 | averwave-4 |
|---|---|---|---|
| force= 0 | -475.32 eV | wave 2.0 | wave 1.0 |
When the C-H length is a little shorter than the experimental values, ele0's motion becomes unstable.
Because like Table 4 and Fig.31, attracting power of carbon against electron 0 is very weak ( cf = 158, compare it with 1403 of Table 7 ).
On the other hand, ele4's orbit is more attracted to C nucleus.
( cf 633 - 499 = 134, compare it with 219 -199 = 20 in Table 7 )
As a result, both electrons' motions become unstable when C-H distance is 9500 MM (= 0.950 × 10-10 meter ).
(Fig.33') If hydrogen becomes too close to carbon, methane is unstable

| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| ele 0 | 6415 | 0 | 0 | nuc 6415 | V -79.7 | cf -851 | rf 0 | wn 2.0 |
| ele 4 | 1064 | 0 | 2932 | nuc 3103 | V -46.29 | cf 1005 | rf 2573 | wn 0.803 |
| afel 0 | 6415 | 0 | 0 | nuc 6415 | V -76.58 | cf -891 | rf 0 | wn 2.0 |
| afel 4 | -1274 | 0 | 2932 | nuc 3197 | V -49.37 | cf -786 | rf 1883 | wn 1.197 |
| H0 nuc | total V | averwave-0 | averwave-4 |
|---|---|---|---|
| force= 0 | -503.98 eV | wave 2.0 | wave 1.0 |
Furthermore, when C-H bond length becomes shorter, electron 0 is attracted to H nucleus instead of original C nucleus ( cf -851 ).
This means carbon structure of methane is broken, when C-H is 9000 MM.
On the other hand, ele4's orbit is more attracted to C nucleus ( cd 1005 - 786 = 219 ).
So both electron's orbit become unstable in this case.
As a result, when internuclear distance of methane is 10900 MM, its configuration is most stable.
(Fig.34) If C-H length becomes shoter.

Here we explain how C-H bond length influences the stability of H nucleus, briefly.
(Fig.A-1) Repulsive force against H nucleus.
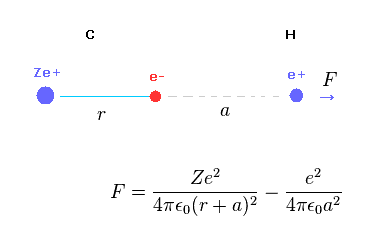
Fig.A-1 shows the total (repulsive) force F acting on hydrogen nucleus.
C nucleus Ze+ acts as repulsive, and C electron acts as attractive force against hydrogen nucleus.
(Fig.A-2) When distance "a" is long.
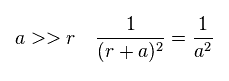
When the ditance "a" between C electron and H nucleus is much longer than "r", the difference between "r+a" and "a" becomes small.
In this case, total charge of carbon in Fig.A-1 is close to +(Z-1)e.
So the hydrogen nucleus tends to be repelled by C nucleus.
(Fig.A-3) When distance "a" is short.
But the distance between C electron and H nculeus is very short, the attractive force by C electron is stronger due to inverse square Coulomb's law.
As a result, when C-H bond length is very short, H nucleus cannot keep stable position.
( And H electron cannot be stabe, either. )
This is one of important reasons why C-H bond length is 1.090 × 10-10 m.
Water (H2O) is indispensable for maintaining our lives.
But even now, we don't know about the important properties of water well using the conventional quantum mechanical methods.
For example, we don't know why water density becomes lower again, when it becomes ice at atomic and electron levels.
So it is very interesting to investigate these mysteryous mechanisms of water using Bohr's orbit based methods.
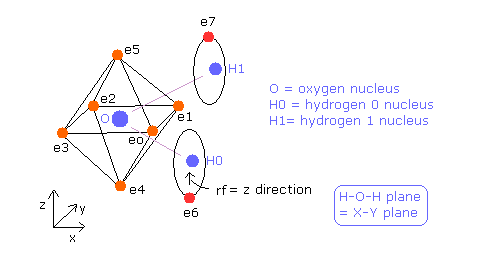
(Fig.35) Estimated Water (H2O) model.
Here we use sample JAVA program below to investigate water structure.
Water molecule (H2O) JAVA program.
In this program, +X(MM), +Y(MM), +Z(MM) mean relative coordinate with respect to each nucleus to which each electron is the closest.
Electron 0-5 belong to oxygen atom, as valence electrons, and electron 6 belongs to H0 nucleus, electron 7 belongs to H1 nucleus.
Basically O nuc, H0 nuc, H1 nuc, ele 0-3 are on the same x-y plane.
And e0-e1, e2-e3, e4-e5, and e6-e7 form pairs, so you can change only coordinates of ele 0, ele 2, ele 4, and ele 6 in textboxes.
Based on these values, the remaining coordinates are automatically determined.
Other methods are almost same as methane ( see this page ).
(Fig.36) Water (H2O) structure.
The average single O-H bond energy of the water is 9.6066 eV (=926.9 kJ/mol) / 2 = 4.8033 eV.
So the total energy of H2O is -433.103 (O) - 2 × 13.606 (H) - 9.6066 (bond energy) = -469.92 eV.
Here 433.103 eV is total ionization energy of oxygen 6 valence electrons.
And 13.606 eV is ionization energy of ground state of hydrogen atom.
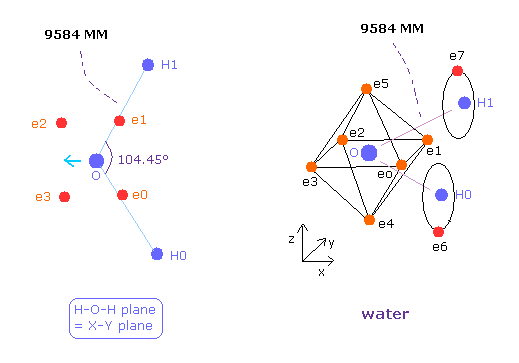
The O-H bond length of H2O is 9584 MM (= 0.9584 × 10-10 meter).
The H-O-H angle is 104.45 degrees, which is a little larger than 90 degrees.
Different from tetrahedral structure of carbon, 6 valence electrons of oxygen are already arranged at symmetric positions with respect to nucleus ( For example, e0-e2, e1-e3.. ), and its rotation radius is smaller than carbon.
So we use this H2O structure as it is.
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| ele 0 | 3130 | -3366 | 0 | nuc 4596 | V -147.33 | cf 5459 | rf 0 | wn 1.983 |
| ele 1 | 3130 | 3366 | 0 | nuc 4596 | V -147.33 | cf 5459 | rf 0 | wn 1.983 |
| ele 2 | -3250 | 3250 | 0 | nuc 4596 | V -145.05 | cf 6184 | rf 0 | wn 2.018 |
| ele 3 | -3250 | -3250 | 0 | nuc 4596 | V -145.05 | cf 6184 | rf 0 | wn 2.018 |
| ele 4 | 331 | 0 | -4585 | nuc 4596 | V -144.5 | cf 6218 | rf 0 | wn 1.999 |
| ele 5 | 331 | 0 | 4585 | nuc 4596 | V -144.5 | cf 6218 | rf 0 | wn 1.999 |
| ele 6 | 350 | -580 | -4340 | nuc 4392 | V -31.11 | cf 285 | rf 1377 | wn 0.869 |
| ele 7 | 350 | 580 | 4340 | nuc 4392 | V -31.11 | cf 285 | rf 1377 | wn 0.869 |
| aele 6 | -752 | 842 | -4340 | nuc 4484 | V -34.14 | cf -228 | rf 1221 | wn 1.131 |
| O nuc FX,FY,FZ | H0 nuc On, Hn | total V | averwave-0 | averwave-6 |
|---|---|---|---|---|
| force = 0, 0, 0 | force = 1, 16 | -936.02 eV | wave 2.00 | wave 1.00 |
According to Virial theorem, total potential energy V is twice the total energy E.
( Total V = = -469.92 × 2 = -939.84 eV. )
So the computing result of Table 10 is good.
And hydrogen electron's motion (= ele 6 ) is almost stable. ( cf = 285 and a-cf = -228 ).
This "cf" is the force acting on each electron toward O nucleus.
We aim at the condition in which total forces against O and H nculei are almost zero, and average de Broglie waves are almost 2.0 ( e0-5 ), 1.0 ( e6 ) in Table 10.
Like CH4 case,
to get e0-5 average de Broglie waves (= averwave-0 ), we compute potential energy and forces only inside oxygen atom.
(Fig.37) Electron distribution change in H2O
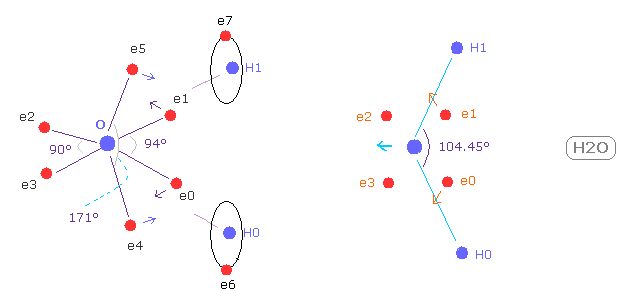
As shown in Fig.37, if H-O-H angle (= 104.45 degree ) is bigger than 90 degree of octahedral structure, e0 and e1 move outward, attracted to hydrogen nuclei.
As a result, e0 - O - e1 angle becomes wider than 90 degree.
Following this formal change, e4 - O -e5 angle becomes smaller than original 180 degree.
As a result, repulsive force by hydrogen nuclei is cancelled out by these configuration change.
( e4 and e5 pull O nucleus toward H atoms. )
In Table 1, we fix the distance between O nucleus and six valence electrons ( nuc = 4596 MM ).
And we fix ele 4 and ele 5's coordinates, and change only ele 0 ( ele 1 ), and ele 4 ( ele 5 ).
In this condition, when e0 - O - e1 angle becomes 94 degree, and e4 - O - e5 angle becomes 171 degree, its potential energy becomes the lowest (= -936.02 eV ), which is almost same as experimental value of -939.84 eV .
(Fig.37') Electron configuration change is blocked, when H-O-H is 90 degree.
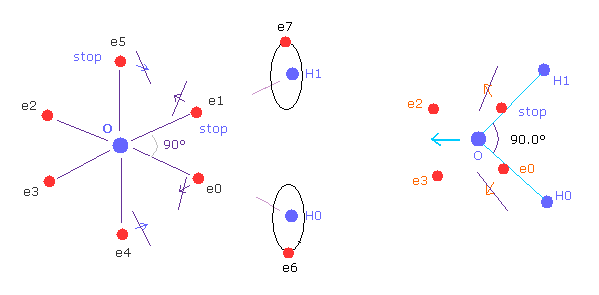
On the other hand, if H-O-H angle is 90 degree, electron e0 and e1 cannot move outward, so e4 and e5 cannot move, either.
Because, O-e0 and O-el lines are on the same lines of O-H0 and O-H1 from the beginning.
So configuration change to cancel repulsive force of H nuclei does NOT happen.
Furthermore, this repulsive force by H nuclei becomes stronger when 90 degree than that of 104.45 degree, due to its sharp angle.
So H-O-H angle of water cannot be 90 degree, due to the strong repulsive force and lack of configuration change.
( The trick of H-O-H angle, 104.45 exists in this configuration change. )
(Fig.37'') Sulfur tetrafluoride ( SF4 ).
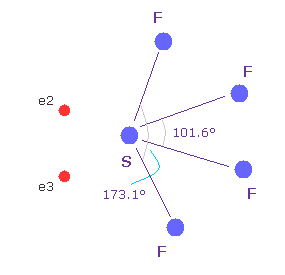
Similar configuration change is seen in sulfur tetrafluoride (= SF4 ).
Sulfur (= S ) has six valence electrons like oxygen.
Due to the strong electronegativity of fluorine, sulfur's electrons are attracted toward fluorines and one side of electron density of S becomes weaker, which causes configuration change.
This mechanism is a little different from H2O above, but their configuration change is similar.
( The important difference between fluorine and hydrogen is seven outer electrons of F tend to repel other electrons as other valence electrons increase, while H is attracted to them. )
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| ele 0 | 3000 | -3483 | 0 | nuc 4596 | V -147.25 | cf 5456 | rf 0 | wn 1.984 |
| ele 1 | 3000 | 3483 | 0 | nuc 4596 | V -147.25 | cf 5456 | rf 0 | wn 1.984 |
| ele 2 | -3250 | 3250 | 0 | nuc 4596 | V -145.05 | cf 6182 | rf 0 | wn 2.016 |
| ele 3 | -3250 | -3250 | 0 | nuc 4596 | V -145.05 | cf 6182 | rf 0 | wn 2.016 |
| ele 4 | 450 | 0 | -4574 | nuc 4596 | V -144.54 | cf 6223 | rf 0 | wn 1.998 |
| ele 5 | 450 | 0 | 4574 | nuc 4596 | V -144.54 | cf 6223 | rf 0 | wn 1.998 |
| ele 6 | 340 | -597 | -4380 | nuc 4433 | V -30.74 | cf 279 | rf 1351 | wn 0.87 |
| ele 7 | 350 | 580 | 4340 | nuc 4392 | V -31.11 | cf 285 | rf 1377 | wn 0.869 |
| aele 6 | -700 | 888 | -4380 | nuc 4523 | V -33.78 | cf -223 | rf 1203 | wn 1.129 |
| O nuc FX,FY,FZ | H0 nuc On, Hn | total V | averwave-0 | averwave-6 |
|---|---|---|---|---|
| force = 0, 0, 0 | force = 4, 21 | -935.20 eV | wave 2.00 | wave 1.00 |
Table 11 shows the results when H-O-H angle becomes bigger (= 110 deg ) than the experimental value (= 104.45 deg ).
In this condition, when the angles of e0-O-e1, and e4-O-e5 are 98 and 168 degrees, its potential energy becomes the lowest (= -935.2 eV ).
But as H-O-H angle becomes bigger, oxygen valence electrons cannot interact with both H nuclei.
As a result, the potential energy becomes higher, which means unstable H2O molecule.
So H-O-H angle of 104.45 degree is equilibrium point.
(Fig.38) The difference between C-H and O-H bond.
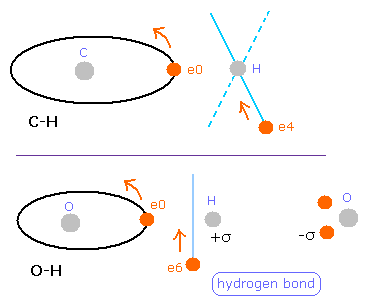
But different from C-H bond of methane (= Table 7 ), this hydrogen electron is a little attracted to oxygen atom ( 285 - 228 = 57 )
( Of course, these absolute value is about "200", which is similar to methane. )
Probably, this strong attractive force by O nucleus is related to hydrogen bonds.
And actually, H2O breaks into OH- + H+ more easily than methane.
H2O is more stable, when hydrogen bond is formed with other water molecules than it is solitary.
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| ele 0 | 3130 | -3366 | 0 | nuc 4596 | V -148.13 | cf 5245 | rf 0 | wn 1.980 |
| ele 1 | 3130 | 3366 | 0 | nuc 4596 | V -148.13 | cf 5245 | rf 0 | wn 1.980 |
| ele 2 | -3250 | 3250 | 0 | nuc 4596 | V -145.19 | cf 6199 | rf 0 | wn 2.021 |
| ele 3 | -3250 | -3250 | 0 | nuc 4596 | V -145.19 | cf 6199 | rf 0 | wn 2.021 |
| ele 4 | 370.5 | 0 | -4582 | nuc 4596 | V -144.6 | cf 6230 | rf 0 | wn 1.999 |
| ele 5 | 370.5 | 0 | 4582 | nuc 4596 | V -144.6 | cf 6230 | rf 0 | wn 1.999 |
| ele 6 | 390 | -750 | -3894 | nuc 3984 | V -34.26 | cf 425 | rf 1639 | wn 0.834 |
| ele 7 | 390 | 750 | 3894 | nuc 4984 | V -34.26 | cf 425 | rf 1639 | wn 0.834 |
| aele 6 | -849 | 849 | -3894 | nuc 4075 | V -38.26 | cf -336 | rf 1389 | wn 1.166 |
| O nuc FX,FY,FZ | H0 nuc On, Hn | total V | averwave-0 | averwave-6 |
|---|---|---|---|---|
| force = 0, 0, 0 | force = 1, 12 | -944.4 eV | wave 2.00 | wave 1.00 |
When O-H bond length is shorter, repulsive force against O nucleus becomes stronger.
To cancel this repulsive force, six valence electrons need to move toward H atom.
So the oxygen octahedral structure breaks, when O-H length is shorter.
This distortion appears as the bigger difference of de Broglie wave number.
(Fig.39) Oxygen structure breaks.
And H atom electron 6 is more strongly attracted to O nucleus ( cf 425 - 336 = 89 ).
And the absolute value of these forces (= about "400" ) are bigger.
So H atom electron's orbit is also unstable like methane molecule.
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| ele 0 | 3000 | -3483 | 0 | nuc 4596 | V -149.02 | cf 4953 | rf 0 | wn 1.978 |
| ele 1 | 3000 | 3483 | 0 | nuc 4596 | V -149.02 | cf 4953 | rf 0 | wn 1.978 |
| ele 2 | -3250 | 3250 | 0 | nuc 4596 | V -145.36 | cf 6199 | rf 0 | wn 2.023 |
| ele 3 | -3250 | -3250 | 0 | nuc 4596 | V -145.36 | cf 6199 | rf 0 | wn 2.023 |
| ele 4 | 527 | 0 | -4566 | nuc 4596 | V -144.78 | cf 6244 | rf 0 | wn 1.997 |
| ele 5 | 527 | 0 | 4566 | nuc 4596 | V -144.78 | cf 6244 | rf 0 | wn 1.997 |
| ele 6 | 570 | -800 | -3423 | nuc 3561 | V -38.38 | cf 637 | rf 1994 | wn 0.800 |
| ele 7 | 570 | 800 | 3423 | nuc 3561 | V -38.38 | cf 637 | rf 1994 | wn 0.800 |
| aele 6 | -771 | 931 | -3423 | nuc 3630 | V -43.38 | cf -546 | rf 1538 | wn 1.201 |
| O nuc FX,FY,FZ | H0 nuc On, Hn | total V | averwave-0 | averwave-6 |
|---|---|---|---|---|
| force = 0, 0, 0 | force = -1, 22 | -955.11 eV | wave 2.00 | wave 1.00 |
When O-H bond length is much shorter (= 8500 MM ), oxygen structure needs to be more broken to cancel out the repulsive force by H nucleus.
And H electron orbit needs to incline ( cf 637, -546 ) unnaturally.
The difference between forces acting on ele 0 and ele 4 become bigger ( cf are 4953 and 6244 ) compareing Table 10 ( cf 5459 and 6218 ).
This means time period of six electrons' orbits become irregular.
(Fig.39') Oxygen-like atom
Surprisingly, in the other oxygen-like atoms, sulfur (S), Selenium (Se), and Tellurium (Te), which have six valence electrons,
H-S-H, H-Se-H, and H-Te-H angles are 92.1, 91.0, and 89.5 degrees, respectively. ( = almost 90 degrees).
So in these oxygen-like atoms, the six valence electrons can be said to be arranged almost "octahedrally".
In the case of oxygen, the hydrogen atom is closer to the oxygen atom than other oxygen-like atoms.
So, the repulsive force by hydrogen nuclei is so strong that the water (H2O) can not keep "octahedral" structure to make O nucleus stable.
( For example, in the 92 degree case of SH2 , these repulsive forces are less than one-third of H2O of 104.45 degree . )
(Fig.39'') Sulfur hexafluoride, SF6 = octahedron.
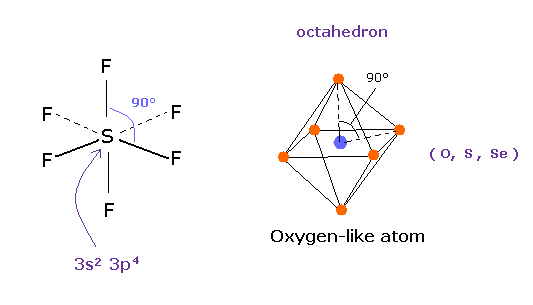
According to the quantum mechanics, sulfur (S) has six valence electrons like oxygen atom.
( 3s × 2 + 3p × 4 = 6. )
And stable sulfur hexafluoride is known to have just octahedral structure, in which F-S-F angle is just 90 degree.
This result clearly indicates, 3s2 3p4 state claimed by quantum mechanics is wrong, and symmetric repulsive Coulomb force among six electrons is right.
Breaking all bonds ( 6 × C-H + C-C ) of ethane requires 2826.1 kJ/mol (= 29.29 eV)
So the ground state energy of ethane (8 carbon valence electrons + 6 hydrogen atoms) becomes -29.29 -148.024 × 2 -13.606 × 6 = -406.974 eV
(148.024 eV is the sum of 1-4th ionization energies of the carbon atom. )
According to the Virial theorem, the total potential energy (tV) becomes 2 × -406.974 = -813.948 eV.
The C-C and C-H bond lengths are 15351 MM, and 10940 MM, respectively. (1 MM = 10-14 meter).
And C-C-H angle is 111.7 degrees.
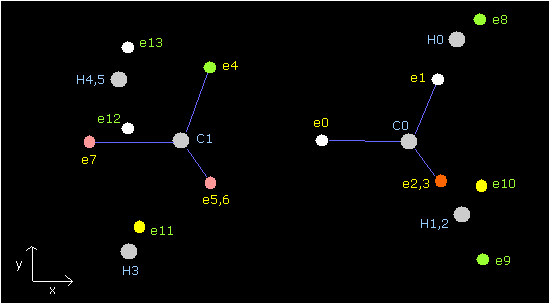
(Fig.40) Periodic motions of ethane's electrons (H3C-CH3)
As shown in Fig.40, the ethane molecule consists of a pair of the 1st and 2nd versions of methane.
Between two carbon nuclei, the four electrons are attracted by another nucleus avoiding each other.
Different from above methane C-H bond, both carbon atoms have the same speed and same oscillating period.
So if possible, we should think about C-C bond as it is.
Here we try to express the ethane molecule using the next sample JAVA program.
( See also True nature of C-C and C=C bonds. )
Sample JAVA program of ethane (Virial theorem)
(If you copy and paste the program source code inside into a text editor, you can easily compile and run this.)
In this program, the central charge (+4e = +6e -2e ) is supposed to be +4.22.
So de Broglie's wave is just 2.00, if the "tetrahedral" structure of carbon is completely kept.
(Fig.41) distribution of ethane's electrons (H3C-CH3)
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | -6285 | 0 | 0 | 6285 | 1880 | 0 | 0 | 0 | 2.006 |
| ele 1 | 2305 | 6019 | 0 | 6445 | 1267 | -6 | 2 | 0 | 1.995 |
| ele 4 | 2235 | 6045 | 0 | 6444 | 2064 | 33 | -6 | -43 | 1.999 |
| ele 5 | 2235 | -3022 | -5235 | 6444 | 2064 | 33 | -34 | 27 | 1.999 |
| ele 6 | 2235 | -3022 | 5235 | 6444 | 2064 | 33 | 40 | 16 | 1.999 |
| ele 7 | -6360 | 0 | 0 | 6360 | 2116 | 0 | 0 | 0 | 2.006 |
| ele 8 | 1800 | 1825 | -3705 | 4505 | 1017 | -247 | -614 | -2 | 1.000 |
| ele 10 | 1800 | 2296 | 3432 | 4505 | 1017 | -247 | 309 | -530 | 1.000 |
| ele 11 | 800 | 1975 | 3900 | 4444 | 1416 | -172 | -298 | 0 | 1.000 |
In Table 14, the total potential energy becomes -813.37 eV, which is almost same as the experimental value -813.948eV.
The average distance between electron (8-13) and each hydrogen nucleus is (4505 + 4444) / 2 = 4474.5 MM, which is almost 4500 MM.
Due to the repulsive force of another carbon, the "tetrahedral" structures of carbons are a little broken.
de Broglie's waves are a little different from 2.000. (The error is ± 0.005 (or 0.006))
We choose the conditions when total forces acting on C0 nuc, C1 nuc and H0 nuc is almost zero.
About the force acting on H1 nucleus , CnH3 should be less than about 400, if possible.
( This CnH3 value is positive due to each hydrogen electron's motion, but it is better this value should be small as possible considering nuclear stability. )
Next we choose the value 16500 in the scrollbar and click the C-C (MM) button.
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | -6300 | 0 | 0 | 6300 | 2049 | 0 | 0 | 0 | 2.010 |
| ele 1 | 2315 | 6020 | 0 | 6449 | 1261 | -8 | 3 | 0 | 1.995 |
| ele 4 | 2290 | 6050 | 0 | 6468 | 2082 | 25 | -4 | -42 | 2.000 |
| ele 5 | 2290 | -3025 | -5239 | 6468 | 2082 | 25 | -34 | 25 | 2.000 |
| ele 6 | 2290 | -3024 | 5239 | 6468 | 2082 | 25 | 39 | 17 | 2.000 |
| ele 7 | -6380 | 0 | 0 | 6380 | 2119 | 0 | 0 | 0 | 2.016 |
| ele 8 | 1900 | 1600 | -3750 | 4498 | 1042 | -233 | -567 | -3 | 1.000 |
| ele 10 | 1900 | 2447 | 3260 | 4498 | 1042 | -233 | 287 | -489 | 1.000 |
| ele 11 | 800 | 1876 | 4110 | 4588 | 1358 | -158 | -234 | 1 | 1.000 |
Basically when the repulsive forces of the four nuclei (three hydrogen nuclei + another carbon nucleus) are balanced, the carbon nucleus becomes stable.
But when the C-C length is longer than the balanced length, the influence of another carbon nucleus becomes weaker. (Fig.42, upper panel)
As a result, the balance of the four repulsive forces breaks down, the "tetrahedral structure" is more broken to make the carbon nuclei stable (= FX, FY, FZ of C0,1 are small).
In Table 15, the maximum error is 0.010 in C0 electrons, 0.016 in C1 electrons, which is bigger than the control of Table 14.
This 0.010 value cannot be smaller.
If you try to make this error 0.010 smaller, 1.995 of ele1 wave must be smaller to keep C0 nucleus stable.
And the total potential energy (tV) is -806.74 eV, which is higher than the experimental value (-813.948 eV)
So the C-C bond in Table 15 is weaker than the control.
(Fig.42) balance of forces of ethane (H3C-CH3)
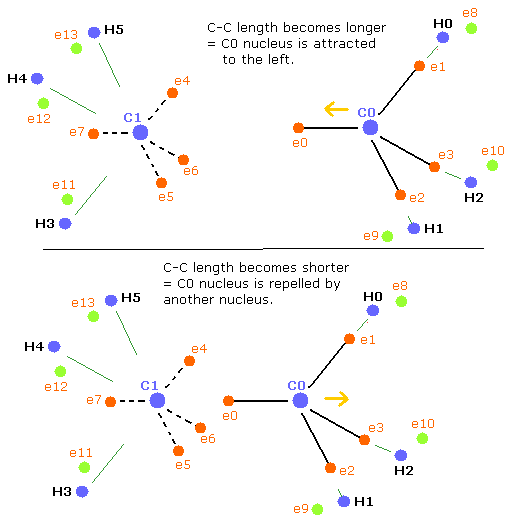
Next we choose the value 14000 in the scrollbar and click the C-C (MM) button.
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | -6190 | 0 | 0 | 6190 | 1592 | 0 | 0 | 0 | 1.996 |
| ele 1 | 2350 | 6070 | 0 | 6509 | 1192 | -9 | 3 | 0 | 2.003 |
| ele 4 | 2235 | 6100 | 0 | 6496 | 1993 | 42 | -8 | -43 | 2.007 |
| ele 5 | 2235 | -3050 | -5282 | 6496 | 1993 | 42 | -33 | 29 | 2.007 |
| ele 6 | 2235 | -3049 | 5282 | 6496 | 1993 | 42 | 42 | 14 | 2.007 |
| ele 7 | -6280 | 0 | 0 | 6280 | 2188 | 0 | 0 | 0 | 1.991 |
| ele 8 | 1800 | 1825 | -3705 | 4505 | 1011 | -246 | -609 | -2 | 1.002 |
| ele 10 | 1800 | 2296 | 3432 | 4505 | 1011 | -246 | 307 | -526 | 1.002 |
| ele 11 | 800 | 1945 | 3800 | 4343 | 1470 | -174 | -327 | 0 | 0.999 |
when the C-C length is shorter (=Table 16) than the balanced length, C0 nucleus is repelled by another nucleus, but on the other hand, C1 nucleus is closer to e0 electron.
So C1 nucleus is attracted to the right, and becomes unstable.(Fig.42, lower panel)
As a result, the "tetrahedral structure" is more broken to make the carbon nuclei stable (= FX, FY, FZ of C0,1 are small).
In Table 16, the maximum error is 0.009, which is bigger than the control of Table 14.
If you try to this de Broglie wave 1.991 of ele7 close to 2.000, you need to put electron 11 ( 12, 13 ) more close to C1 nucleus.
But in this unnatural state, CnH3 value (= force acting on H3 nuc ) becomes unnaturally bigger than 430.
Next we choose the value 13500 in the scrollbar and click the C-C (MM) button, which makes C-C length much shorter.
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | -6180 | 0 | 0 | 6180 | 1354 | 0 | 0 | 0 | 1.987 |
| ele 1 | 2305 | 6095 | 0 | 6516 | 1190 | 2 | 0 | 0 | 2.007 |
| ele 4 | 2200 | 6200 | 0 | 6578 | 1934 | 55 | -10 | -46 | 2.024 |
| ele 5 | 2200 | -3100 | -5369 | 6578 | 1934 | 55 | -35 | 32 | 2.024 |
| ele 6 | 2200 | -3099 | 5369 | 6578 | 1934 | 55 | 45 | 14 | 2.024 |
| ele 7 | -6300 | 0 | 0 | 6300 | 2173 | 0 | 0 | 0 | 1.984 |
| ele 8 | 1800 | 1850 | -3680 | 4494 | 1011 | -247 | -623 | -1 | 1.000 |
| ele 10 | 1800 | 2261 | 3442 | 4494 | 1011 | -247 | 312 | -538 | 1.000 |
| ele 11 | 850 | 1980 | 3840 | 4403 | 1446 | -173 | -315 | 0 | 0.999 |
In Table 17, C0 nucleus is more repelled by another nucleus, and C1 is more attracted by e0 electrons. (Fig.42, lower)
So, to make the carbon nuclei stable (= FX, FY, FZ of C0,1 are small), "tetrahedral" structures need to be more broken than the upper case of Table 14.
In Table 17, the maximum error is is much bigger than the control of Table 14.
Here, the hydrogen electrons 11,12,13 are supposed to be closer to C nucleus than the hydrogen electrons 8,9,10. (Fig.40 upper).
(So the +X and +Y coordinates of ele 11 need to be positive.)

2013/3/6 updated. Feel free to link to this site.