Top page ( correct Bohr model )
Truth of electromagnetic fields.
All true atomic structures.
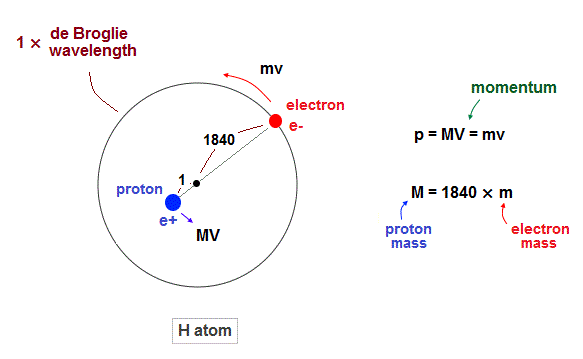
(Fig.1) Hydrogen atom. Proton (= nucleus) is 1840 times heavier than electron.

Proton is about 1840 times heavier than an electron.
So proton (= nucleus ) is almost at rest in hydrogen atom.
But of course, from the fact of reduced mass, proton is thought to be moving by Coulomb force inside atoms. Due to total momentum conservation, proton's momentum is always just the opposite of electron ( MV = mv ).
According to de Broglie theory ( wavelength = h/momentum ), both electron and proton's de Broglie wavelength should be the same. But they are not.
As seen in Fig.13, proton is confined to about 1840 times smaller region than the electron's orbit. So proton is almost at rest.
(Fig.2) While electron is orbiting, proton is almost "stationary".
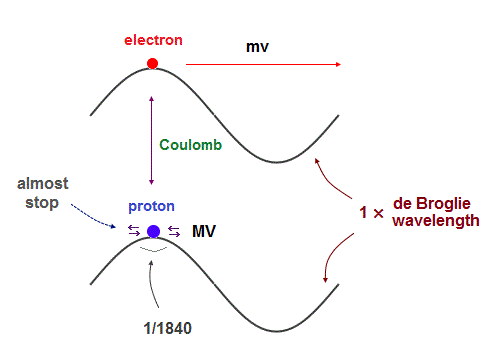
Their same (= opposite ) momentums should generate the same de Broglie wavelength.
But proton's moving area is 1840 times shorter than electron's orbit.
So the proton is considered to be oscillating in almost the same place, instead of orbiting, like a electron inside neutron.
In fact, proton's magnetic moment (= g-factor × angular momentum ) is NOT proton's Bohr magneton, which is so weak that proton's actual "spinning" can influence its magnetism.
On the other hand, large magnetic moment of electron (= 658 times proton ) indicates it is due to electron's orbital motion, NOT by unrealistic tiny spin.
As light electron has to move to the opposite side of nucleus in which electron's uniform oscillation cannot be kept. So an electron must rotate around with de Broglie waves, not oscillate.
(Fig.3) Spin is too weak ! Coulomb interaction causes ferromagnet !
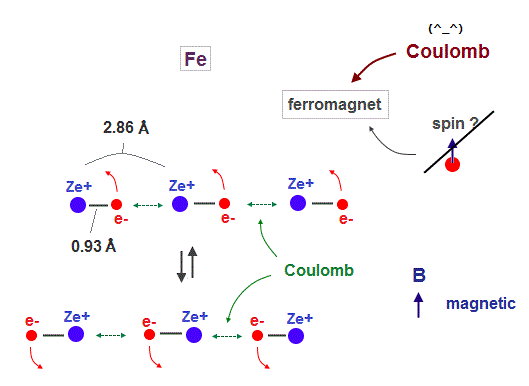
It is known that iron (= Fe ), Ni, Co can be ferromagnet even at room temperature.
As I said, spin magnetic moment (= Bohr magneton ) is too weak (= 1 K ) to cause ferromagnet at 1043 K in Fe.
So we have to consider other strong interactions such as Coulomb forces.
In Fig.18, iron atomic raius (= 0.93 Å ) is suited for synchonizing with neighboring atoms.
Like in this section, if we designate de Broglie wavelength ( Fe = 4 ), atomic structure ( Fe = regular hexahedron ), and total 1-8th ionization energies, we can know the atomic radius ( Fe = 0.93 Å ). See this.
We use lattice constant of iron, which direction is most involved in ferromagnet.
(Fig.4) Titanium electron is too influenced by other neuclei.
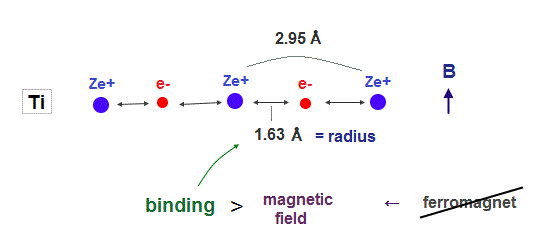
In atoms such as titanium, which electron's number is smaller than iron, their atomic radius is longer due to weak central charge Ze+.
In this case, each valence electron is too much restricted by neighboring nuclei, which prevents them from responding to external magnetic fields. As a result, ferromagnet cannot be seen in this titanium.
(Fig.5) Copper has 11 valence electrons. ← Too shrinked !
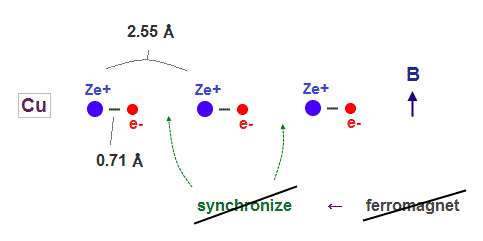
On the other hand, copper has as many as 11 valence electrons.
So its atomic radius shrinks too much to sinchronize with other nuclei under external magnetic field.
In Copper, each electron is more influenced by other valence electrons belonging to the same atom, which prevents them from synchronizing with external magnetic fields.
As a result, Fe, Ni, Co have atomic radius, which length is just suited to cause stable ferromagnet.
(Fig.6) Maximum orbits = midpoint lines + 2 (= two perpendicular orbits )
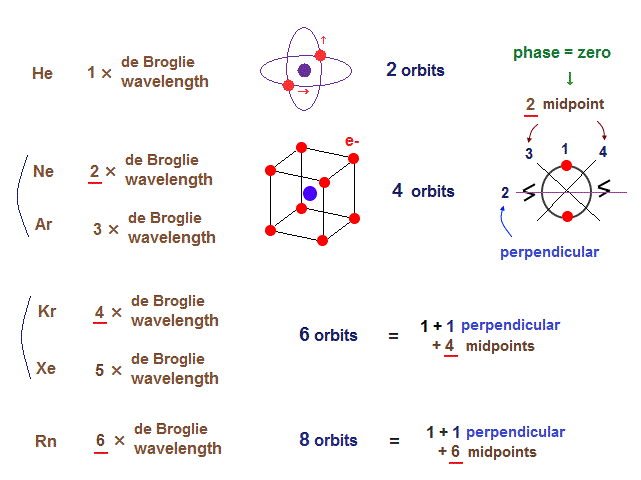
On this page, we show all atomic structures and the number of midpoint lines ( related to de Broglie wavelength ) influences the number of maximum orbital number in the periodic table.
In this section, we prove atomic structure based on de Broglie wavelength can explain various molecular bond length.
(Fig.7) Rough estimtion of helium-like structure.
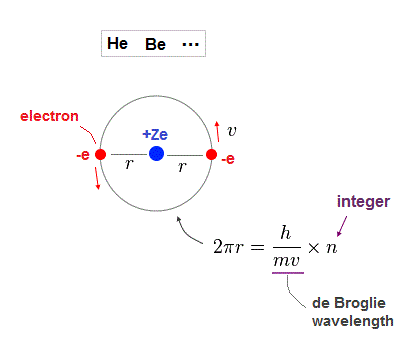
As shown on this page, when two electrons in the same orbit, it gives a little different energy values.
( Two perpendicular orbits give the exact helium ground state energy. ).
But approximately, Fig.7 simple helium-like model can be used in estimating atomic radius.
One orbital length is supposed to be an integer times de Broglie wavelength in Fig.38.
Nuclear central charge is +Ze, atomic radius is "r". "v" is electron's velocity
(Fig.8) Coulomb force = centrifugal force.
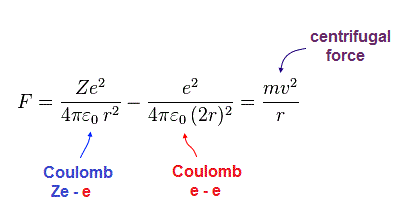
In Fig.8, the sum of Coulomb force ( from nucleus and another electron ) is equal to the centrifugal force.
(Fig.9) Total energy E = sum of potential and kinetic energies.
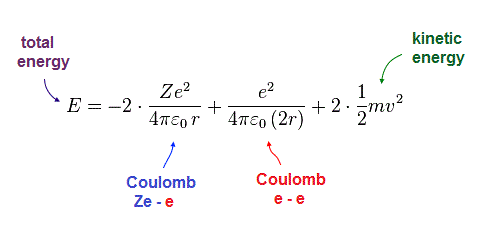
Total energy E is the sum of all potential and kinetic energies.
Solving Fig.7-9, we can obtain the equations of atomic radius "r" and total energy "E".
(Fig.10) Atomic radius "r" and total energy E depend on de Broglie wavelength "n".
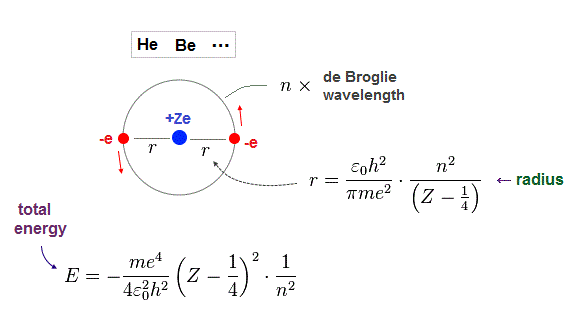
Just for calculation, we use Bohr radius and ground state energy of hydrogen atom.
(Fig.11) Hydrogen Bohr radius and ground state energy.
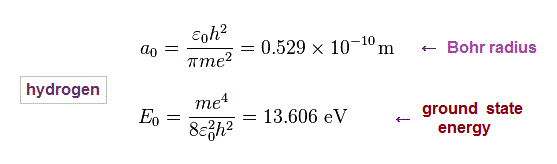
Beryllium has two valence electrons in n = 2 orbits.
We suppose the sum of 1st and 2nd ionization energies of Be is total energy E in n = 2 orbits.
Inserting E = 27.5 eV (= sum of 1st, 2nd ionization energies ) and n = 2 (= de Broglie wavelength ) into the result of Fig.10, we obtain Fig.12.
(Fig.12) Beryllium effective central charge Z = 2.26. ← good !
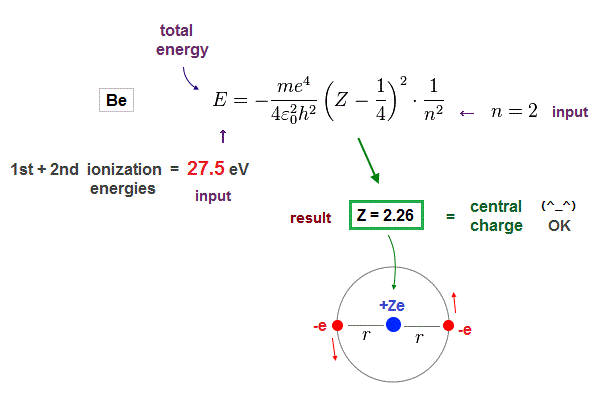
As seen in Fig.12, when we input n = 2 as de Broglie wavelength, it gives reasonable effective central charge Z = 2.26.
This central charge is the sum of +4e Be nucleus and two 1s electrons. ( +4e -2e = +2e )
So the sum of them should be close to "2". Due to electron 1s shell gap, it's a little bigger than 2.
(Fig.13) Atomic radius when 2 × de Broglie wavelength in Be.
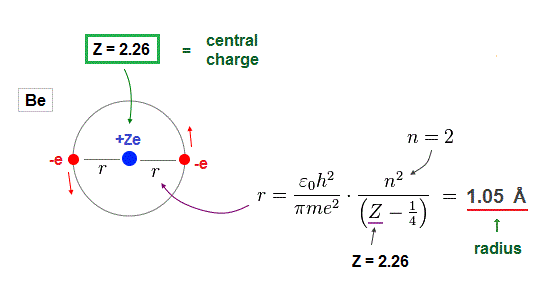
Furthermore, when Be valence electrons are in 2 × de Broglie wavelength orbits, their orbital radius becomes 1.05 Å, which can explain experimental bond length properly.
(Fig.14) Experimental Be-Be bond length = 2.22 Å
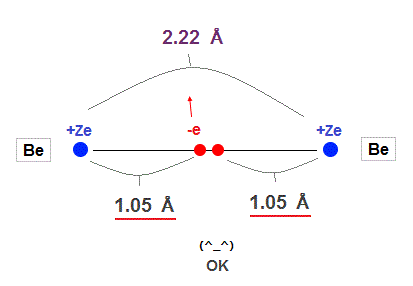
In this site, the experimental value of Be-Be bond length is 2.22 Å ( 1 Å = 1.0 × 10-10 m ).
This value is almost 2.10 Å = 2 × 1.05 Å of calculation value in
Fig.13 !
So the concept of de Broglie wavelength is valid in Beryllium molecular bond !
(Fig.15) n = 1 → Central charge Z is too small, and radius is too short !
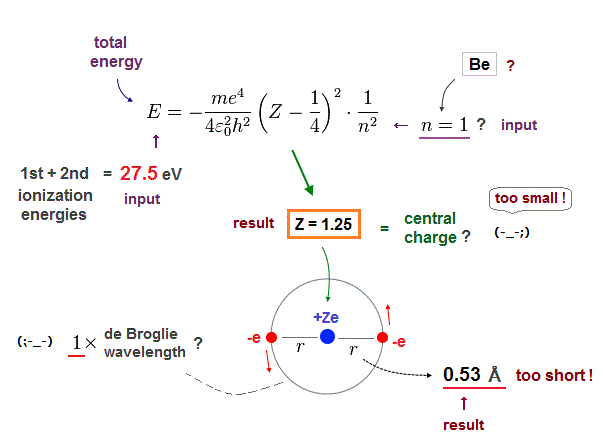
Next we suppose Beryllium valence electrons are in 1 × de Broglie wavelength orbits and input n = 1 instead of n = 2. The same ionization energy (= 27.5 eV ) is used as total energy E.
As shown in Fig.15, in this case, the effective central charge becomes too small ( Z = 1.25 ).
Central charge must be bigger than 2, so this result is inconsistent with the actual Beryllium !
Orbital radius is also too short (= 0.53 Å ).
2 × 0.53 Å = 1.06 Å is much shorter than the actual bond length ( 2.22 Å ).
(Fig.16) Central charge Z is too big, and radius r is too short in n = 3 !
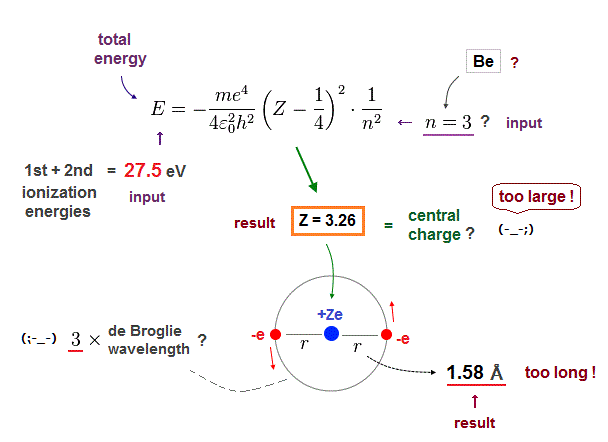
Next, if we input n = 3 instead of n = 2 into these equations.
This case also gives unreasonable results.
The effective central charge Z = 3.26 is too big, with respective to "2".
And atomic radius 1.58 Å is too long to explain actual Be-Be bond length (= 2.22 Å ).
As a result, we can prove two valence elecrons of Beryllium in 2 × de Broglie wavelength orbit !
(Fig.17) Carbon = four valence electrons.
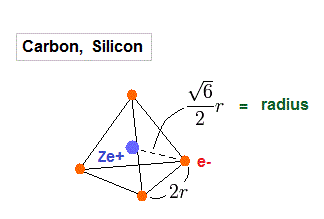
Carbos and silicons have four valence electrons.
So we assume regular tetrahedron like Fig.17 to get atomic radius.
(Fig.18) Total potentian energy V.

Total potential energy is the sum of energies among Ze+ center and four electrons.
(Fig.19) Coulomb force toward center acting on each electron.
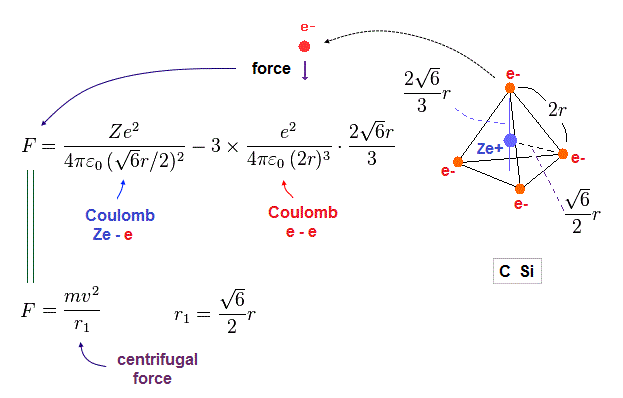
Fig.19 is the Coulomb force toward center acting on each electron.
We suppose this force is equal to centrifugal force.
(Fig.20) n × de Broglie wavelength orbit !
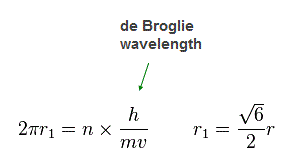
Again we suppose each orbit satisfies an integer (= n ) times de Broglie wavelength.
(Fig.21) Total energy E and radius r in carbon-like atoms
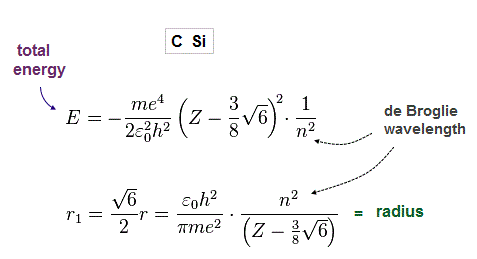
From Fig.8-20, we obtain total energy E and radius r, as shown in Fig.52.
(Fig.22) True atomic radius r and effective central charge Z in Carbon.
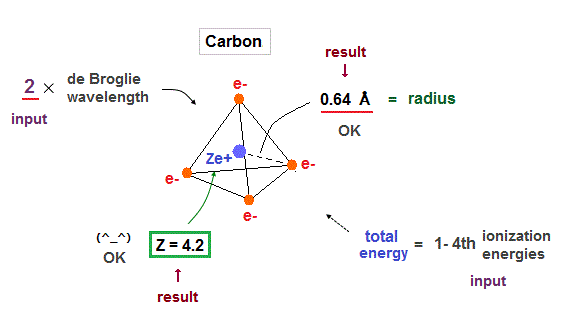
In this table, we suppose the sum of 1-4th ioniztion energies as total energy of n = 2 carbon valence electrons.
Inputting E = 148 eV and n = 2 into Fig.21, we get radius 0.64 Å and Z = 4.2, which is very good.
(Fig.23) Experimental values of C-H, C-C bond length.
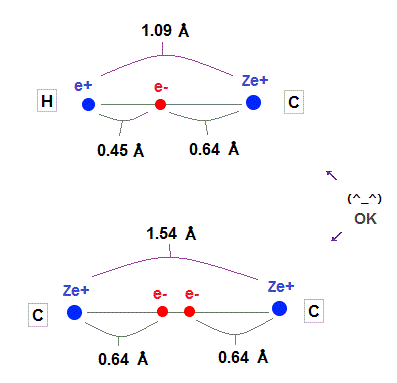
As shown on this and this, experimental values of H-C and C-C bond length is 1.09 Å and 1.54 Å
Carbon atomic radius (= 0.64 Å ) fits these experimental values very well.
Hydrogen atomic radius (= 0.45 Å ) shrinks, and is a little shorter than Bohr radius (= 0.53 Å ) due to attraction of carbon's nucleus.
(Fig.24) If carbon valence electrons are in 1 or 3 de Broglie wavelength, wrong radius !
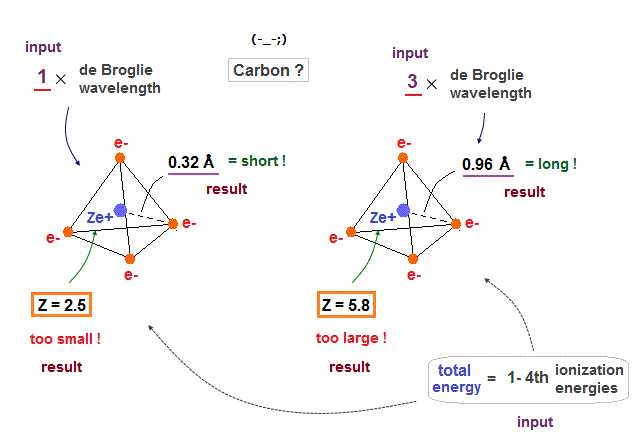
If we suppose carbon's valence electrons are in 1 or 3 de Broglie wavelength orbits, it gives "too short" or "too long" atomic radius, compared with the experimental bond lenghs.
Effective central charge (= Z ) are also "too small" (= 2.5 ) or "too large" (= 5.8 ) compared with the proper value of "4". So we find four valence electrons of carbon are in 2 × de Broglie wavelength orbits.
(Fig.25) Silicon radius and central charge, when 3 × de Broglie wavelength.
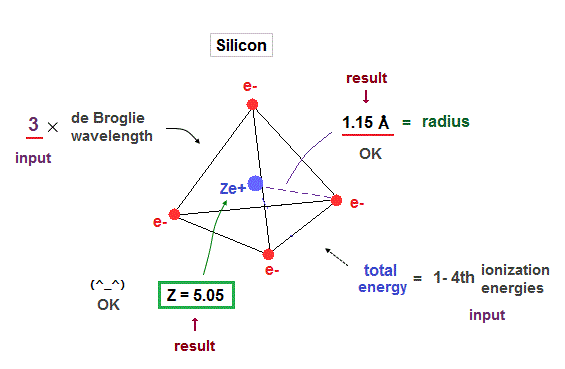
When we suppose four valence electrons of silicon are in 3 × de Broglie wavelength orbits, it gives good results. Effective central charge (= 5.05 ) is a little bigger than carbon, due to larger gap.
(Fig.26) When silicon valence electrons are in 2 or 4 de Broglie wavelength orbits ..
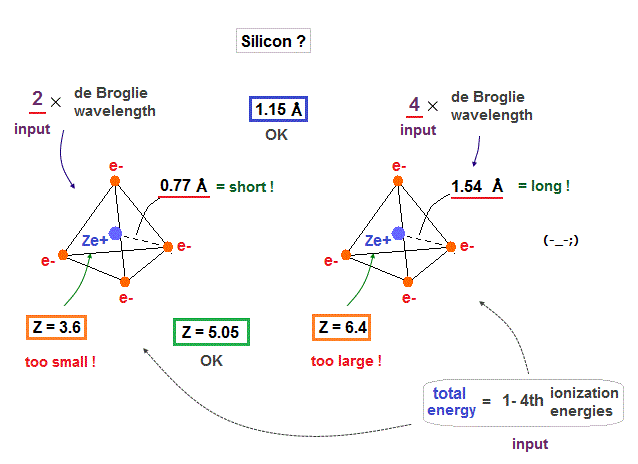
If we suppose silicon valence electrons are in 2 or 4 de Broglie wavelength orbits, their effective charges become "too small" ( Z = 3.6 ) or "too big" ( Z = 6.4 ), compared with 4.
(Fig.27) Experimental value of Si-Si bond length.
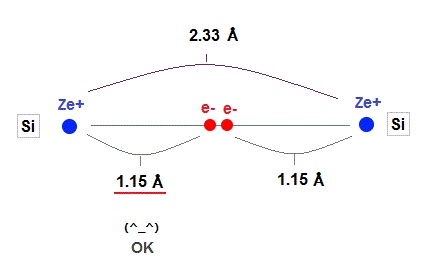
As shown in this, the exeprimental value of Si-Si bond length is 2.33 Å.
Atomic radius in 3 × de Broglie wavelength is just consistent with this experimental bond length.
1.15 × 2 = 2.30 Å = 2.33 Å, when 3 × de Broglie wavelength !
On the other hand, radii in 2 or 4 de Broglie wavelength are inconsistent with the experimental values !
(Fig.28) Why silicon's effective central charge (= 5.05 ) is bigger than carbon (= 4.2 ) ?
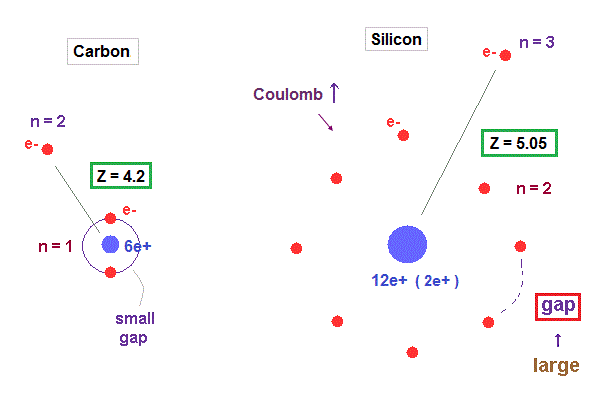
Though both carbon and silicon have the same four valence electrons, their effective central charges (= Z ) are different. Because larger gaps are open in silicon inner shell.
As shown in Fig.28, gap between n = 1 electrons are much smaller than that of n = 2 electron shell, which difference gives larger effective central charge Z in silicon.
(Fig.29) Regular octahedron = Oxygen-like.
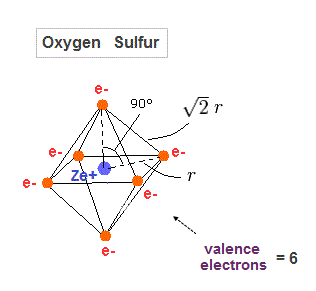
Oxygen and sulfur have six valence electrons, so we can suppose they have "octahedral" electron distribution.
(Fig.30) Total potential energy V in oxygen-like atoms.
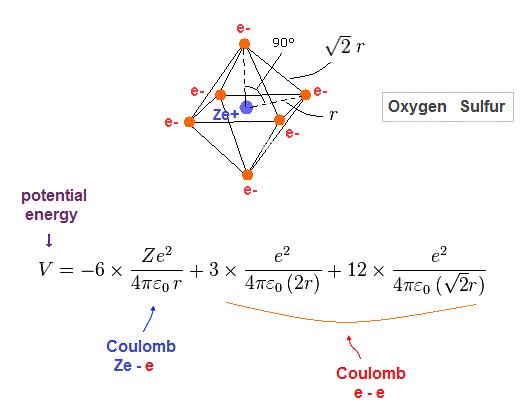
Fig.30 is total potential energy V in oxygen-like atoms.
(Fig.31) Force acting on each electron
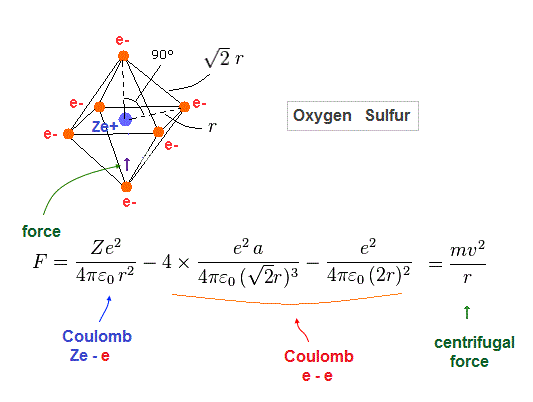
Fig.31 is Coulomb force acting on each electron in oxygen-like atoms.
We suppose this is equal to centrifugal force.
(Fig.32)
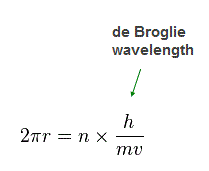
Again we suppose each orbit is n × de Broglie wavelength.
(Fig.33) Total energy E and radius of oxygen-like atoms
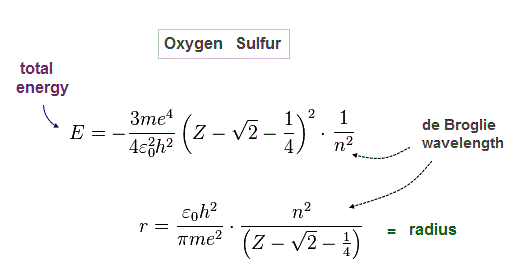
Solving Fig.30-32, we get Fig.64.
(Fig.34) Oxygen ( Sulfur ) is 2 (3) × de Broglie wavelength.
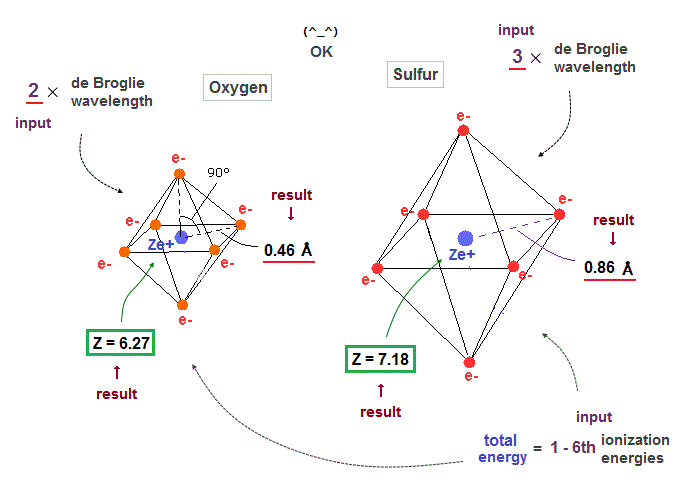
When we suppose oxygen valence electrons are 2 × de Broglie wavelength orbits, it gives good central charge ( Z = 6.27 ), which is close to "6".
Due to larger gap in inner shell, the effective central charge Z of sulfur becomes a little larger (= 7.18 ) than oxygen.
(Fig.35)
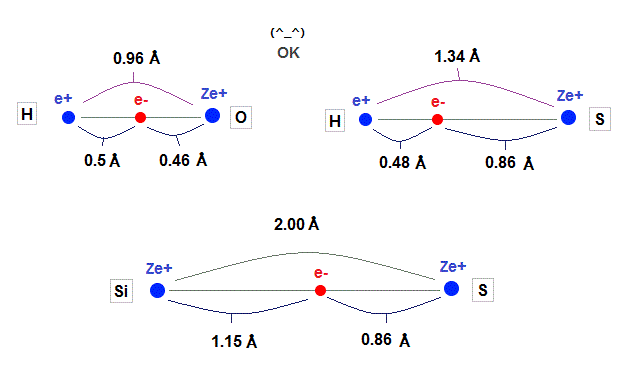
Using calculation results by de Broglie wavelength in oxygen-like and silicon, we can explain experimental bond length, as shown in Fig.35.
(Fig.36) When two atoms approach too close, repulsion among "electrons" get bigger.
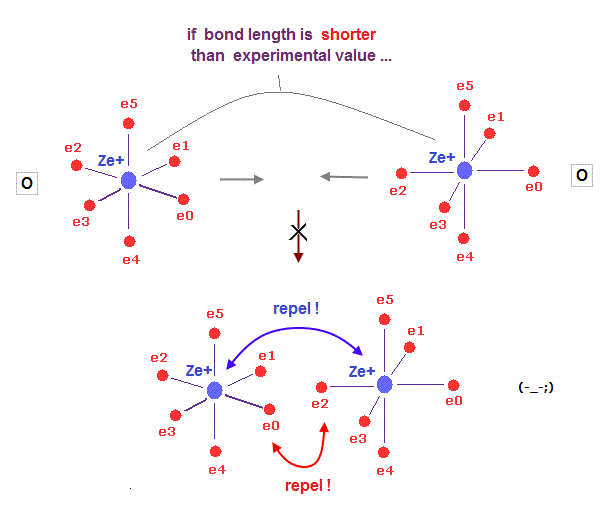
What determines each molecular bond length ?
On this page, we prove Coulomb repulsion among electrons becomes stronger, when the distance between two atoms is shorter than the experimental value in H2, using Virial theorem.
As two nuclei are closer to each other, electrons in both atoms are attracted toward the center of two atoms. This repulsion among electrons gets stronger in shorter bond length.
(Fig.37) H - F bond is very tight and stable. Why ?
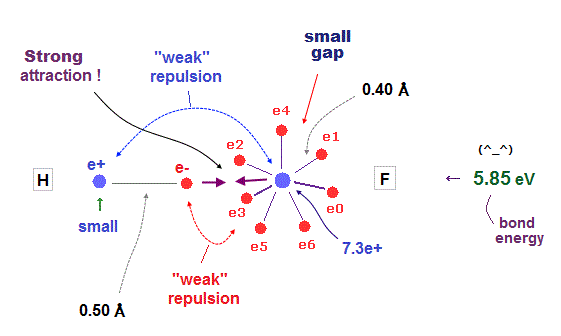
It is known that hydrogen tends to be attracted and bound to fluorine tightly and stably.
Fluorine has seven valence electrons and large effective central charge, so its radius is very short.
So there are only very small gaps among seven valence electrons in F.
To avoid electrons and pass through this small gap, another atom must have a small number of valence electrons.
This is the reason why hydrogen atom with only one electron tends to be bound to fluorine tightly.
(Fig.38) F-F bond is very unstable due to strong repulsion among electrons.
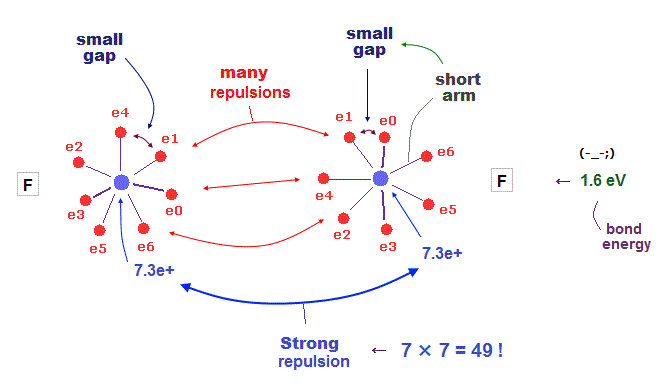
When two fluorines are bound to each other, this F-F bond tends to be unstable.
Because both these two fluorines have very small electrons' gaps.
To cancel strong internuclear (= 7e × 7e ) repulsions, both-side electrons have to approach another nucleus. But very small gaps among valence electrons in F prevent them.
This is the true mechanism of molecular bond length.
If you run this java program, you can know radius (= nuc ) and central charge (= Z ).
| Atom | electrons | de Broglie | Radius | charge Z |
|---|---|---|---|---|
| H | 1 | 1 | 0.45 Å | Z = 1.0 |
| Be | 2 | 2 | 1.05 Å | Z = 2.2 |
| C | 4 | 2 | 0.64 Å | Z = 4.2 |
| N | 5 | 2 | 0.53 Å | Z = 5.2 |
| O | 6 | 2 | 0.46 Å | Z = 6.3 |
| F | 7 | 2 | 0.40 Å | Z = 7.3 |
| Al | 3 | 3 | 1.39 Å | Z = 4.0 |
| Si | 4 | 3 | 1.15 Å | Z = 5.0 |
| P | 5 | 3 | 0.98 Å | Z = 6.1 |
| S | 6 | 3 | 0.86 Å | Z = 7.2 |
| Cl | 7 | 3 | 0.76 Å | Z = 8.2 |
| Atom | electrons | de Broglie | Radius | charge Z |
|---|---|---|---|---|
| Na | 1 | 3 | 2.59 Å | Z = 1.8 |
| Mg | 2 | 3 | 1.74 Å | Z = 2.9 |
| K | 1 | 4 | 3.74 Å | Z = 2.2 |
| Ca | 2 | 4 | 2.60 Å | Z = 3.5 |
| Ti | 4 | 4 | 1.63 Å | Z = 6.1 |
| Cr | 6 | 4 | 1.18 Å | Z = 8.8 |
| Mn | 7 | 4 | 1.04 Å | Z = 10.2 |
| Fe | 8 | 4 | 0.93 Å | Z = 11.5 |
| Co | 9 | 4 | 0.85 Å | Z = 12.8 |
| Ni | 10 | 4 | 0.77 Å | Z = 14.2 |
| Cu | 11 | 4 | 0.71 Å | Z = 15.5 |
| Zn | 12 | 4 | 0.66 Å | Z = 16.8 |
| Atom | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th | Total |
|---|---|---|---|---|---|---|---|---|
| H | 13.606 | - | - | - | - | - | - | 13.606 |
| Be | 9.323 | 18.211 | - | - | - | - | - | 27.534 |
| C | 11.260 | 24.383 | 47.888 | 64.494 | - | - | - | 148.025 |
| O | 13.618 | 35.121 | 54.936 | 77.414 | 113.899 | 138.120 | - | 433.108 |
| F | 17.423 | 34.971 | 62.708 | 87.140 | 114.243 | 157.165 | 185.186 | 658.836 |
| Si | 8.152 | 16.346 | 33.49 | 45.142 | - | - | - | 103.13 |
| P | 10.487 | 19.77 | 30.202 | 51.444 | 65.025 | - | - | 176.928 |
| S | 10.36 | 23.338 | 34.79 | 47.222 | 72.595 | 88.053 | - | 276.358 |
| Cl | 12.968 | 23.814 | 39.61 | 53.465 | 67.8 | 97.03 | 114.196 | 408.883 |

2015/6/7 updated. Feel free to link to this site.