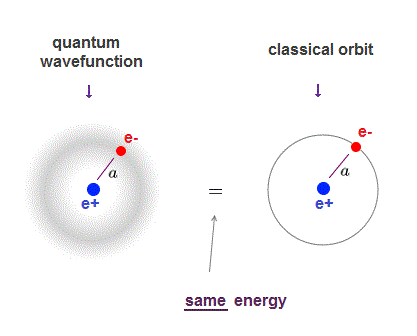
(Fig.1) ↓ Schrödinger's wavefunction = classical orbit

Schrödinger equation of quantum mechanics gives exactly the same energy levels and electron's orbital radius as classical orbit in hydrogen.
Quantum mechanics also uses de Broglie wavelength, which determines the average electron's orbital radius.
The average electron's orbital radius in ground state hydrogen agrees with Bohr radius (= a ) in both quantum mechanics and classical orbit.
So even the lowest-energy electron keeps some distance (= a ) from the nucleus, as far as the orbit is an integer times de Broglie wavelength (= boundary condition in quantum mechanics ).
(Fig.2) ↓ Unreal quantum wavefunction = an electron everywhere !?
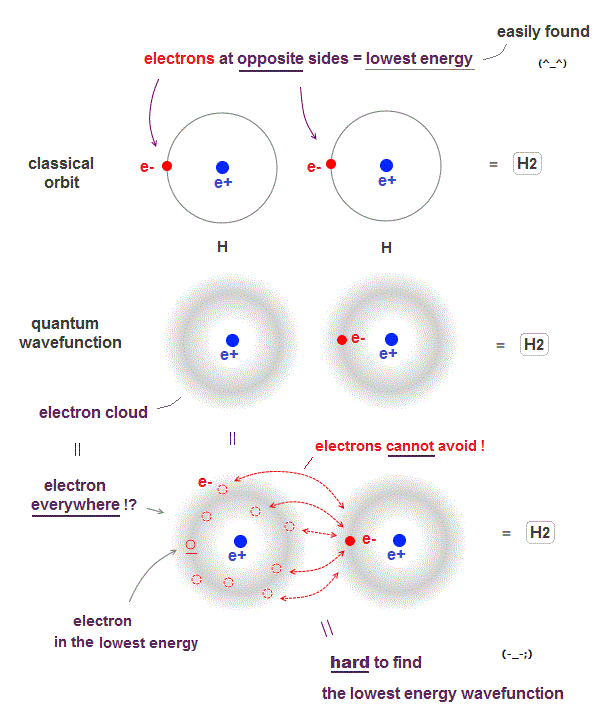
Due to de Broglie wavelenth, an electron keeps some distance from the nucleus in both quantum wavefunction and classical orbit even in the ground state.
When two hydrogen atoms form hydrogen molecule, the lowest energy state is when two electrons just avoid each other as shown in Fig.2 upper.
In classical orbit, we can easily find this lowest energy state in any molecules.
For example, In methane (= CH4 ), the tetrahedral distribution of carbon's four valence electrons is the lowest energy (= electrons avoid each other ), which can be easily found.
The problem is quantum mechanical wavefunction gives vague electron cloud spreading over all space, which means each electron is always everywhere.
If an electron is vague electron cloud, electrons cannot avoid each other in quantum mechanics !
When an electron of one atom approaches another nuclei and another electron moves away to the opposite side, it is the lowest energy state (= Fig.2 upper ).
But quantum wavefunction must always spreads over all space (= electron's probability is Not zero in any points ), which always includes higher-energy electron's positions.
It means classical orbits can easily find the lowest-energy electrons' positions (= useful !), while quantum mechanics must take infinite time to find the lowest-energy fake solution from infinite choices (= useless, impractical ).
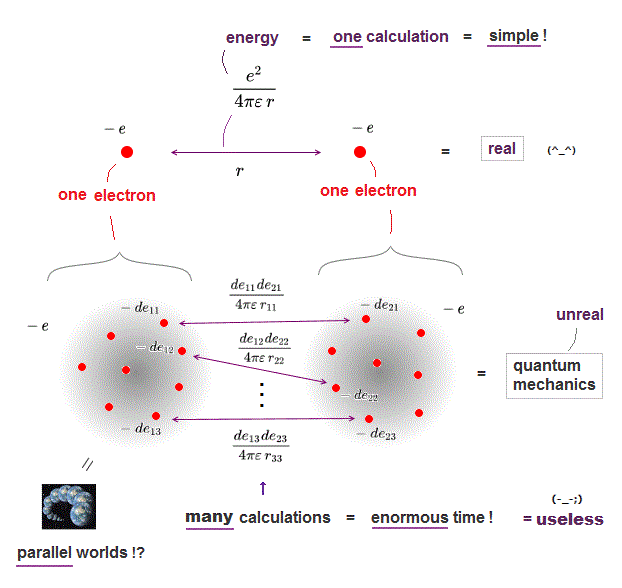
(Fig.2a) ↓ Calculating two charges is impossible in  ?
?
The current basic science is impractical, biologists and chemists ignore quantum mechanics due to useless Schrödinger equation ( this p.1 left ).
In classical physics, calculating force between two charges is very easy, but quantum mechanics can hardly calculate even this simple force !
Quantum mechanics treats each electron as vague cloud spreading over all space, which makes calculating electrons' force impractical in quantum mechanics.
If a single electron is spreading over space like quantum mechanics, electrons cannot avoid each other, which is unreal.
We have to calculate almost infinite patterns of Coulomb energies between small charges inside two electrons' clouds, and sum them up, which takes enormous time ( this p.4, this p.8 ).
On the other hand, in classical electron = point charge, we just do only one calculation of Coulomb force between two electrons, which is much easier, and takes almost no time.
Why must a quantum mechanical electron always spread in all space ? Because Schrödinger equation cannot distinguish between electron particle and de Broglie wave (= field ).
In quantum mechanics, de Broglie relation is expressed as derivative, which becomes infinity when an electron is a point charge = delta function.
But actual electrons are moving particles avoiding each other !
Effective nuclear charge which a helium electron feels is 1.69, bigger than 1, which means two electrons in helium are always avoiding each other ( this p.3, this last ).
And spreading electron clouds in quantum mechanics make it impossible to conserve total energy in multi-electron atoms, so wrong.
(Fig.2b) ↓ Electron's kinetic energy = derivative of wavefunction.
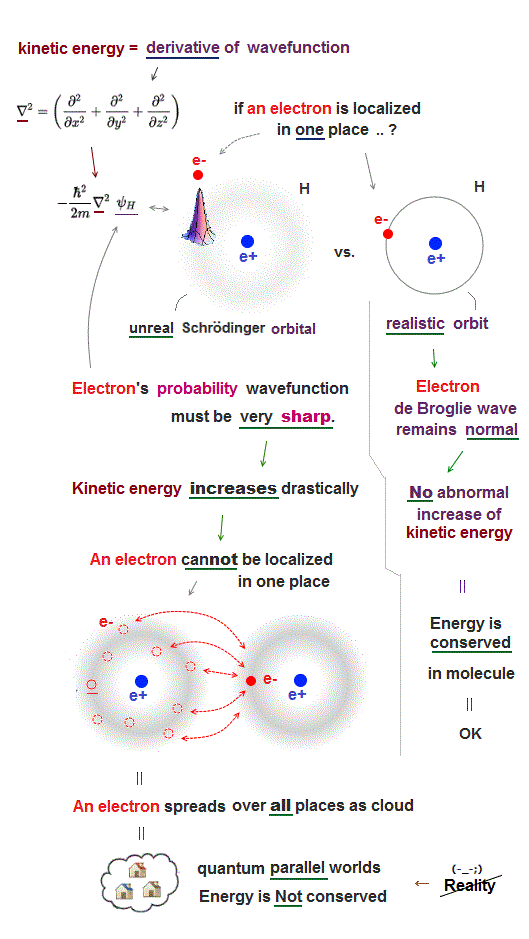
The most crucial difference between quantum mechanics and realistic Bohr model is the definition of a particle and wave.
Quantum mechanics dismissed real entities such as an electron particle and de Broglie wave, instead, it just mixes a partcle and wave as one nonphysical wave function.
Therefore, in quantum mechanics, even a single electron spreads out over all space as fuzzy electron cloud (= whether an electron is a particle or wave is uncertain ).
They claim this fuzzy cloud densities at different areas show "different probabilities" of finding an electron. ← This forced interpretation has No factual grounding.
If quantum mechanical picture is correct, a single particle has to pass through two slits at once like a ghost using fantasy parallel worlds to cause observed interference.
In Bohr's realistic picture, an electron just passes through one of two slits, and de Broglie wave around the electron can pass both slits, which model can naturally explain two-slit interference without relying on fictional quantum parallel worlds.
These quantum electron clouds cannot avoid other electrons, so to get molecular binding energy, quantum mechanics has to rely on "cheating" to lower total energy in unfair way which lowers only kinetic energy by violating energy conservation law and Virial theorem ( this p.3 ).
So quantum mechanical molecular bonds based on cheating have nothing to do with actual molecules, hence physically meaningless. ← Another proof that quantum mechanics is wrong.
Quantum mechanical wavefunctions interpreted as "electron's probability" cannot avoid each other, because the electron cloud wavefunction must be always symmetrically distributed around the nucleus (= hence, the electron's probability also must be evenly distributed around the nucleus ).
If we try to localize each electron to one side of a nucleus to avoid another electron, quantum "electron-probability" wavefunction needs to be sharper at the electron's point, therefore drastically increasing the electron's kinetic energy which is expressed as a derivative of wavefunction.
For example, if we try to express quantum electron as a localized point particle like classical atomic model, the electron's probability wavefunction needs to be sharp delta function at the electron's position where the electron's kinetic energy (= derivative of wavefunction or delta function ) increases to infinity, which cannot form stable molecular bond (= lowering total energy is impossible ).
So the only realistic molecular model obeying energy conservation law by electrons avoiding each other must be like Bohr model where each electron is an actually moving particle and its de Broglie wave is generated around the electron particle (= so separating a particle from its wave is necessary. )
In this realistic Bohr model where an electron particle is separated from de Broglie wave generated around an electron particle, de Broglie wave has nothing to do with the electron's probability wavefunction, hence, an electron particle can be localized in one particular place without sharpening electron's probability wavefunction (= sharper wavefunction means shorter de Broglie wavelength and increasing electron's kinetic energy in unphysical quantum mechanics ) or increasing kinetic energy.
Mixing a electron particle and wave as "one weird probability wavefunction" as seen in quantum mechanical Schrödinger equation is unable to describe actual stable molecules.
(Fig.2c) ↓ Only real moving electrons can get enough attraction.
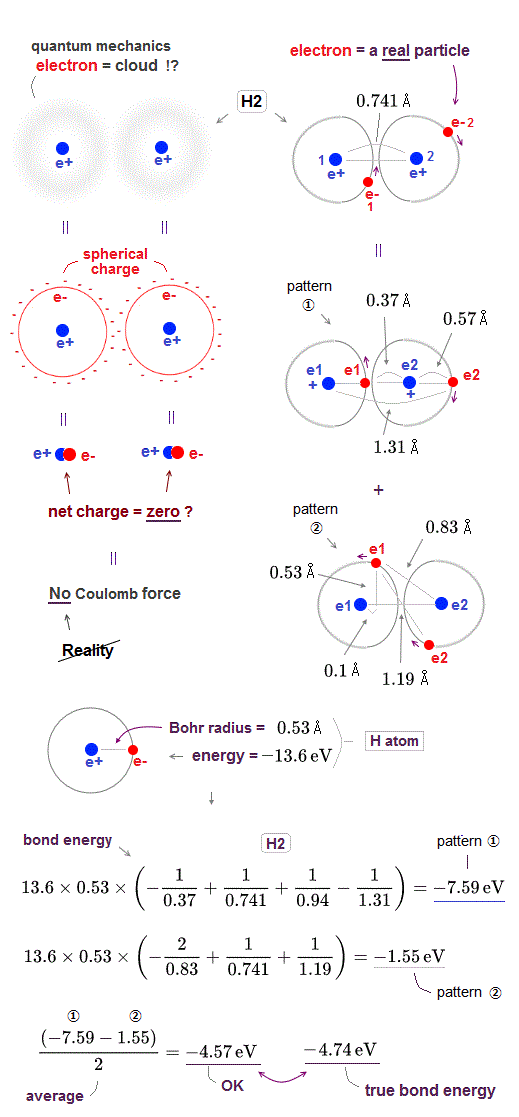
The hydrogen atomic wavefunction of quantum mechanics is expressed as unphysical "electron cloud" where even a single electron must always spread over all space symmetrically around each nucleus.
This unrealistic quantum mechanical electron cloud can neither approach the other positive nucleus nor avoid the other negative electron, so it cannot generate enough "Coulomb attraction" to form molecular bond.
This electron cloud mixing up an electron particle and wave picture as one nonphysical wavefunction is caused by the fact that unrealistic quantum mechanics cannot distinguish a real electron from de Broglie wave in the "medium".
Electron cloud distributed "symmetrically" and evenly around each nucleus is equal to " spherical charge" (= so the center of this quantum electron cloud is just at the same position as a nucleus, overlapping it ) around a nucleus. ← The net charge of electron cloud and nucleus (= overlapping at the same position ) is almost neutral = zero. ← No Coulomb force !
Therefore, quantum mechanical electron cloud cannot generate Coulomb energy enough to bind H2 molecule, and it has to rely on "cheating" where total energy is Not conserved and kinetic energy is lowered illegitimately (= instead of lowering Coulomb potential energy legitimately ) using unreal indistinguishable electrons and nonphysical "exchange energy".
In this quantum mechanical "indistinguishable" electrons, each electron must always exist in all different atoms unrealistically, so quantum mechanical molecule cannot be used as practical basic structual tool.
On the other hand, in the realistic atomic model, each electron is "actually moving" (= able to approach the other positive nucleus and avoid the other negative electron ) to generate Coulomb attractive force enough to form molecular bond.
Here, we roughly estimate how much hydrogen (= H2 ) molecular bond ( Coulomb ) energy is generated by this realistic moving electron model.
The total energy and average electron' orbital radius of hydrogen atom are -13.6 eV and 0.53 Å (= 1 Å = 10-10 m ), respectively. ← We use these values for calculation.
In hydrogen (= H2 ) molecule, the bond length between two hydrogen atoms is 0.741 Å and bond energy is -4.74 eV.
In pattern ①, the electron-1 approaches the nucleus-2 (= distance between the electron-1 and nucleus-2 is the shortest = 0.37 Å ), and the electron-2 avoids the electron-1 to the opposite side of the nucleus-2 (= distance between the electron-2 and nucleus-2 is elongated to 0.57 Å due to repulsive electron-1 ).
The Coulomb potential energy (= total bond energy including kinetic energy using Virial theory ) of this pattern ① between two H atoms 1 and 2 becomes -7.59 eV, which is the sum of Coulomb energy between electron-1 and nucleus-2 (= distance 0.37 Å), two nuclei (= distance 0.741 Å ), two electrons (= distance 0.94 Å ) and the electron-2 and nucleus-1 (= distance 1.31 Å ).
The Coulomb potential energy (= total bond energy ) of this pattern ② between two H atoms 1 and 2 becomes -1.55 eV, which is the sum of Coulomb energy between electron-1 and nucleus-2 (= distance 0.83 Å), two nuclei (= distance 0.741 Å ), two electrons (= distance 1.19 Å ) and the electron-2 and nucleus-1 (= distance 0.83 Å ).
So the average total bond energy of this realistic H2 molecule model becomes -4.57 eV which is good result close to experimental value -4.74 eV.
In H2 molecule, each electron' orbital radius shrinks more, because the number of the central positive nuclei increases to "two" from "one" of hydrogen atom, so considering shorter orbital radius can get this calculation value closer to true H2 molecular bond energy.
We need to consider other factors such as de Broglie wave interference where two orbits of H2 molecule have to be perpendicular to each other at their crossing point to avoid destructive interference which is realistic version of Pauli exclusion principle.
As shown in the pattern ① in the upper figure, the negative electron (= moving particle ) approaching the other positive nucleus and avoiding the other negative electron is the "main generator" of actual molecular bond energy.
So, the unrealistic quantum mechanical electron cloud which cannot approach the other nucleus or avoid the other electron cannot generate enough Coulomb attraction. ← It has to rely on illegitimate cheating. ← Quantum mechanics is false.
From the two basic conditions of Coulomb force (= of course, total energy must be cosnerved ) and electron's orbital length which must be an integer times de de Broglie wavelength to avoid destructive interference, we can know electron's "orbital radius" from which information, we can estimate Coulomb force between atoms and predict the direction in which chemical reaction will proceed.
But in unrealistic quantum mechanical molecule which has No such thing as real "forces", they can neither calculate real forces nor predict how each atomic chemical reaction is going, because they cannot distinguish different atoms or electrons. ← Unbelievable.
In pattern pattern ① of real H2 molecule in the upper figure, the distance between electron-1 (= e1 ) and nucleus-1 is also shorter (= 0.37 Å ) than the original Bohr radius (= 0.53 Å ) of independent hydrogen atom.
Because when the electron-1 approaches the other nucleus-2, the electron-1 is attracted to this nucleus-2 in the opposite direction of nucleus-1.
So the electron-1 needs to be closer to the original nucleus-1 to increase Coulomb attraction between electron-1 and nucleus-1 and overcome the attraction from the other nucleus-2, staying in the orbit around the original nucleus-1.
As a result, the distance between electron-1 and nucleuc-1 becomes shorter in H2 molecule than the original Bohr radius of independent hydrogen atom, and this "shrinking orbital radius" when each electron passes between two positive nuclei (= this electron is attracted in the opposite directions by two positve nuclei ) is one of the main generators of lowering Coulomb potential energy to form real molecular bond.
(Fig.3) ↓ Classical orbit vs. useless quantum molecule = No force.
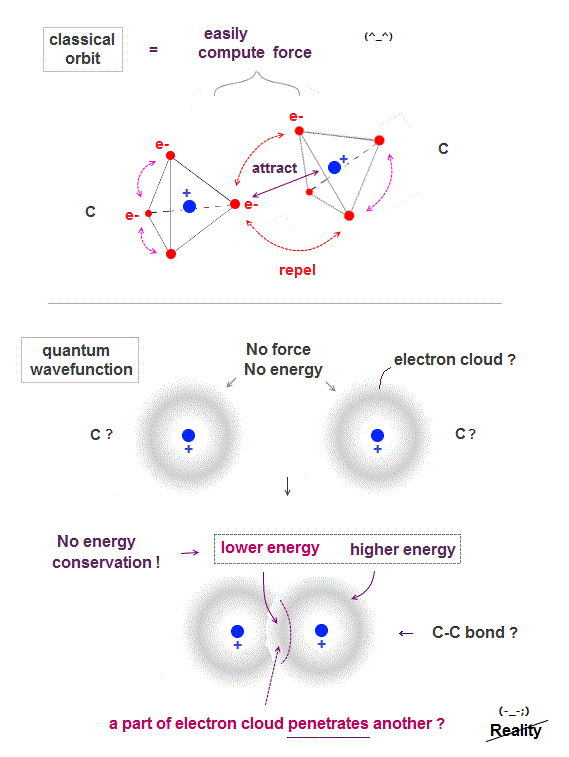
In classical orbit, electrons are point particles separated from each other, so it can easily find the most stable (= the lowest energy ) electrons' position.
The lowest-energy state is when electrons just avoid each other between and inside atoms.
After finding the lowest-energy state, we can easily calculate force between atoms, and predict which direction each atom will move in new chemical reaction.
Quantum mechanical wavefunction is vague electron cloud, which cannot avoid each other, so it's very hard (= impossible ! ) to find the lowest-energy molecular wavefunction.
If a single electron is Not a point particle but spreading over all space as cloud, two electrons don't feel repulsion from each other, when they are outside of each other, as seen in spherical charge.
Only when two wavefunctions penetrate each other (= inside spherical electron charge ), it feels more attraction from another nucleus, causing molecular bond ?
Quantum mechanics needs infinite time to find the lowest-energy wavefunction from infinite choices, artificially changing trial wavefunctions and the amount of electron penetration.
Quantum mechanics cannot calculate "force", which makes itself useless, because "energy" does not tell us "direction" in which atoms will move in chemical direction.
Estimating force is much easier, because we only consider a few electrons between atoms, while when computing energy, we have to consider the "whole orbital" (= all other many electrons involved ).
The worst point of quantum mechanics is its molecule cannot satisfy energy conservation ( an electron penetrating another electron is lower energy than outside ).
(Fig.4) ↓ Overlapped part is lower energy = No energy conservation !
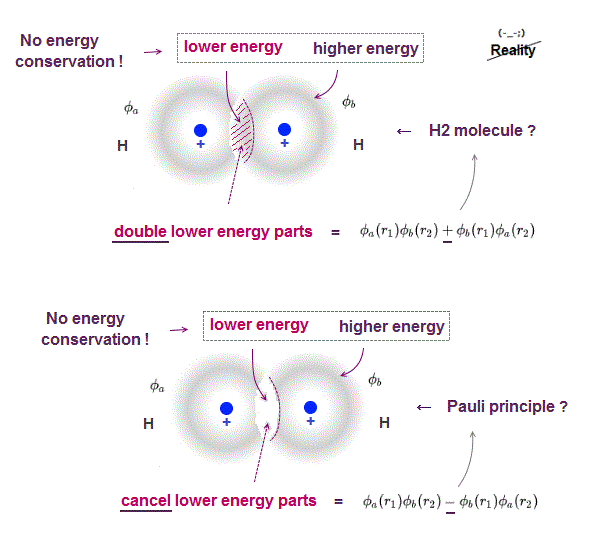
The problem is Schrödinger's atoms cannot satisfy energy conservation law, so unreal.
Even when two hydrogen atoms overlap, each hydrogen's electron energy is conserved only with respect to each nucleus, Not to another nucleus.
A part of electron cloud penetrating another electron cloud feels more attraction , this overlapped wavefunction part (= feels both nuclei ) is lower energy than outside of cloud (= feels only one nucleus ), so total energy is Not conserved in different positions.
When wavefunction is antisymemtric (= when exchanging r1 and r2, it becomes minus ), it causes Pauli exclusion principle, they insist.
In Fig.4 lower (= antisymemtric, Pauli ), overlapped part (= lower energy ) is cancelled, leaving only higher energy part, so the total is higher energy, which causes Pauli repulsion force ?
This Pauli principle by quantum mechanics depends on unreal condition (= energy is Not conserved between overlapped and non-overlapped parts ), so untrue.
See this page.
See this in detail.

2020/3/11 updated. Feel free to link to this site.