トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは存在しない。
近藤効果のページに戻る。
(Eq.1)
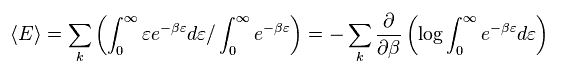
温度 T における 平均のエネルギーは それにボルツマン因子 ( β = 1/kT ) を かけて得られる。
Eq.1 では、 エネルギー (= ε ) は 連続した値としている。
実際の現象では エネルギーは ドブロイ波の整数倍の条件のため 量子化される。
エネルギー ε を 離散的にして、
(Eq.2)
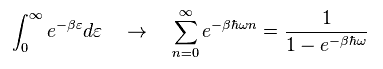
Eq.2 を Eq.1 に代入して、次を得る。
(Eq.3)
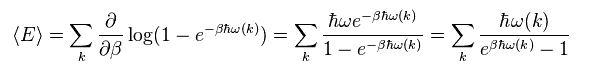
これを "ボーズ・アインシュタイン分布" という。
(Fig.1) パウリの排他原理の原因は "力" ? → "つまらんことは質問するな。"
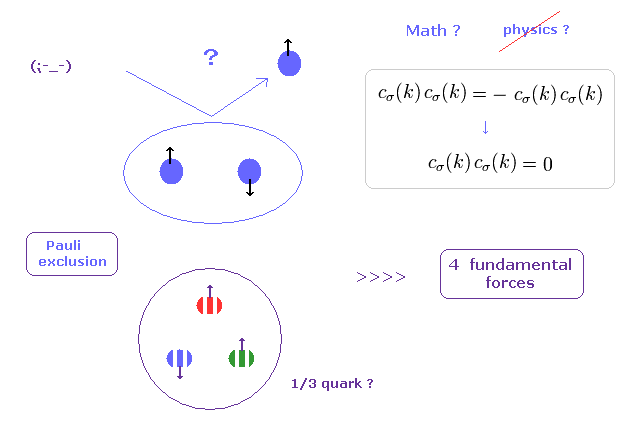
何かしらの物性物理学の教科書を見れば分かるが、一見して それらの本の中には 非現実的な "スピン" の語句で溢れかえっているのが分かる。
しかし 彼らは この スピン とは 何かを決して問おうとはしない。
"パウリの排他原理" は 絶対的な力を持ち、つまり 2つの同じ状態のフェルミ粒子は 同じ場所に どんな状況でも入れない。
( しかし この”同じ場所”という定義が 非常に曖昧である。物理的に 境界線を はっきり定めることもできないのに。)
(Eq.4)
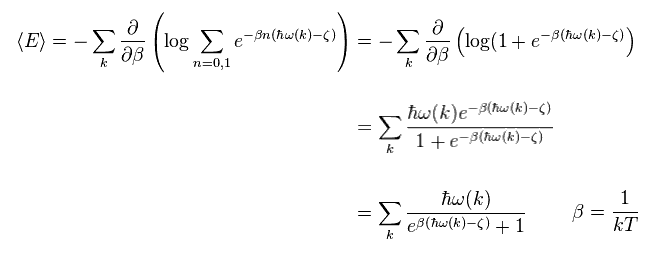
フェルミ・ディラック統計は パウリの排他原理に従う 粒子の分布を表すものである。
つまり これらの粒子数は n は "0" か "1" になる。
Eq.1- Eq.3 のように、Eq.4 では フェルミ・ディラック分布を得た。
このパウリの排他原理は
(Eq.5)
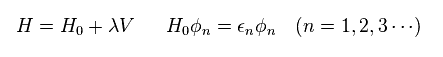
Eq.5 では、 H0 と ε は 自由粒子におけるハミルトニアンと そのエネルギーである。
"V" は 相互作用ハミルトニアンである。
この V は 通常複雑であるため、Eq.5 のような 近似的なハミルトニアン H を用いる。
(Eq.6)
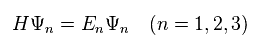
この H (= ハミルトニアン全体 ) の 固有値は "E" で 固有関数は Eq.6 に示すように "Ψ" である。
(Eq.7)
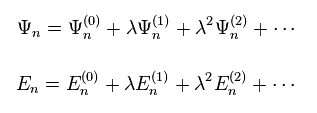
Eq.7 に示したように Ψ と E を λ に関して 展開した。
Ψ(0) と E(0) は 自由粒子の φ や ε と同じである。
Eq.5 と Eq.7 を Eq.6 に代入して、
(Eq.8)
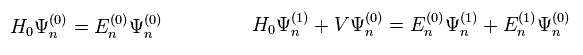
Eq.8 の左は λ がない (= ゼロ次 ) 項である。
Eq.8 右では λ の1次の項のみピックアップした。
(Eq.9)
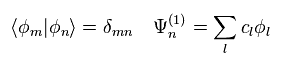
Eq.9 に示すように Ψ を Eq.5 の 固有関数 φ で構成されているとした。
また この φ は 規格直交系であるとする。
(Eq.10)
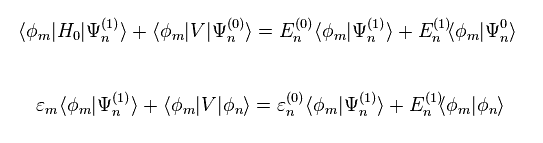
Eq.8 右の式で Eq.9 を用いて、左側から φm を掛けると Eq.10 を得る。
( Eq.5 も 用いる。 )
"m" が "n" に 等しくないとき、Eq.10 の最後の項は ゼロになる。
(Eq.11)
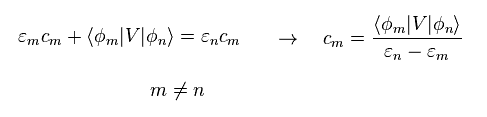
Eq.11 を Eq.9 に代入して、
(Eq.12)
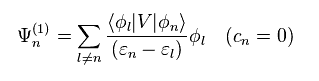
ここで Ψ(1) の "cn" を ゼロとする。
Eq.12 は 一次の摂動である。
(Eq.13)
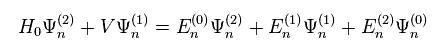
同じように Eq.6 と Eq.7 で 2次の λ までを含む項を ピックアップする。
(Eq.14)
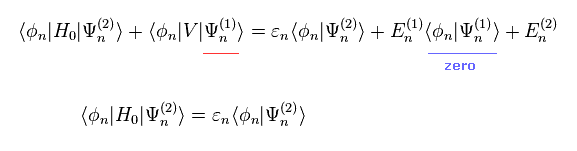
両辺の最初の項は 同じであるため 打ち消し合う。
Eq.12 を Eq.14 に代入して、
(Eq.15)
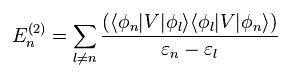
結果的に 次を得る。
(Eq.16)
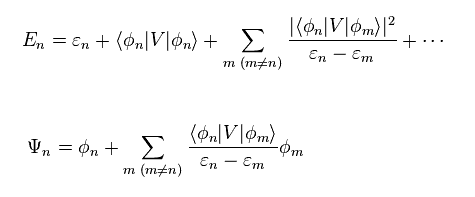
E の1次の摂動 (= 上記の式の右辺の2項目 ) は Eq.10 に φm の代わりに φn を掛けて得られる。
物性物理学の多体系では しばしば 近似的なエネルギーを用いる。
そのため Eq.16 は重要である。
( この公式は 単なる数学の域を超えず また 発散の問題を引き起こす。 )
フェルミの黄金律は 時間に依存するハミルトニアンや摂動をベースにした 遷移確率である。
(Eq.17)
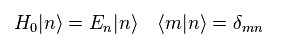
Eq.17 は 自由粒子における 時間に依存しないハミルトニアンとエネルギーである。
ハミルトニアンが 時間に依存する 相互作用部分 (= H'(t) ) を含むとき、シュレデインガー方程式は
(Eq.18)
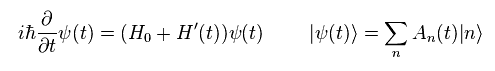
Eq.18 は 次に等しい。
(Eq.19)
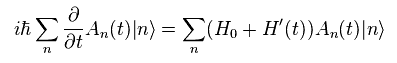
Eq.19 の 左側から 固有状態 "m" を掛けると、
(Eq.20)
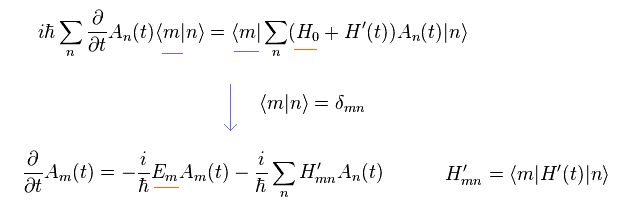
ここで 次を定義する。
(Eq.21)
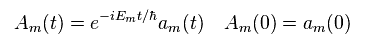
Eq.21 を Eq.20 に代入して、それに 左側から eiEt/h を掛けて、
(Eq.22)
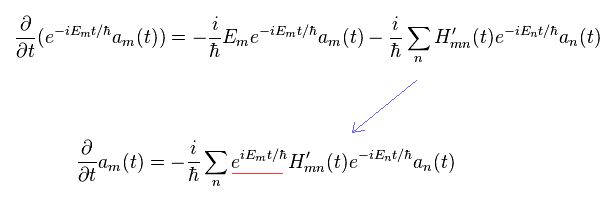
Eq.22 を t' で積分し、 それに e-iEt/h を掛けて、Eq.21 の関係式を用いると、
(Eq.23)
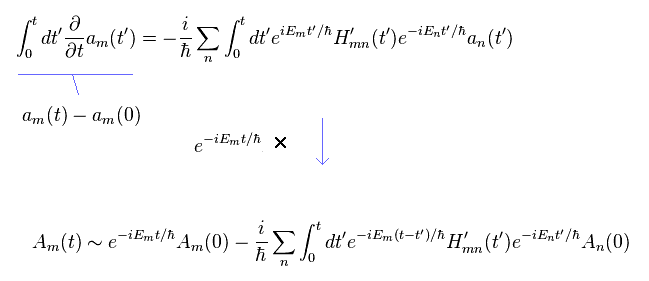
Eq.23 では、右辺で an(t') を近似的に An(0) に変える。
また 次の関係式を使う。
(Eq.24)
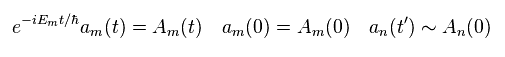
初期状態 ( t= 0 ) を 単純な形 (= δmn ) に定義して Eq.23 の右辺で 2項目 (= 相互作用 ) の部分のみをピックアップすると、
(Eq.25)
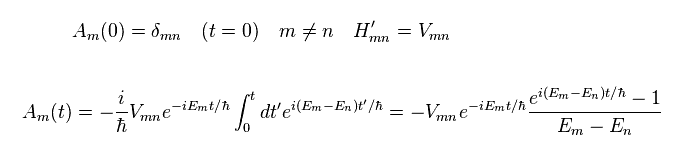
Eq.25 に その複素共役を掛けると 次を得る。
(Eq.26)
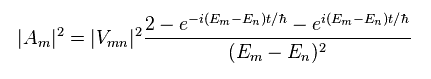
ここで 次の関係式を使うと、
(Eq.27)
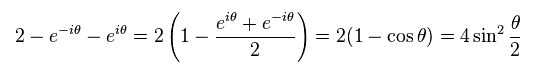
Eq.26 は、
(Eq.28)
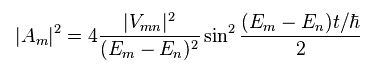
デルタ関数と その公式は
(Eq.29)
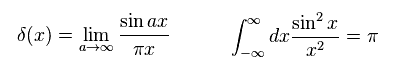
Emn を 次のように定義する。
(Eq.30)
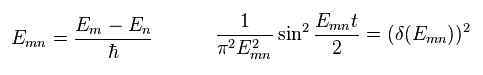
次のような 数学上のトリックを使う。
(Eq.31)
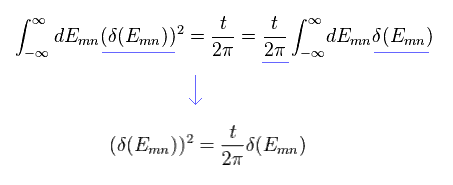
Eq.28 - Eq.31 から 次を得る。
(Eq.32)
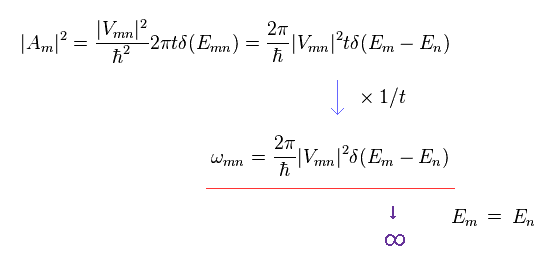
Eq.32 の最初の行で、 デルタ関数の公式を用いて、 デルタ関数内部で Emn の "ħ" 部分を消去できる。
Eq.32 を 時間 "t" で割り、遷移確率 (= フェルミの黄金律 ) を得る。
問題は この種の遷移確率は デルタ関数のため しばしば発散する ということである。
つまり 私達は これら 単なる"数学上"の世界を逃れて 様々な物理現象を
より "リアル"な物で 表すように 早急にすべきである。
( 同じことが 数学上のブラックホールにおける 非現実的な"特異点" などについても言える。)
(Fig.2) 単なる抽象的な 演算子では バライティーに富む 実際の現象を説明できない。
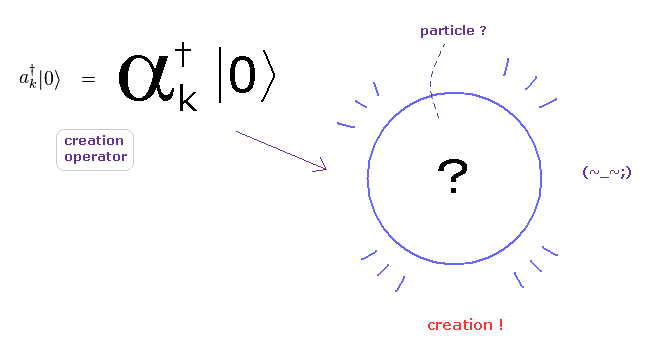
現在の物性物理学、標準模型、ひも理論などの量子論では 様々な物理現象を記述するのに 非常に抽象的な演算子なるものに 完全に頼っている。
このページに見られるように、これらの生成消滅演算子では 実世界の 様々なダイナミックに変化する現象を記述するには どう転んでも 限界がある。
なぜなら これらの生成 (消滅) 演算子では ただ漠然と 空間上に 粒子が生成 (消滅) したことのみを示せるだけで、具体的な変化に富む 時間、場所、位置関係を指定できないからである。
つまり、これらの非常に抽象的な演算子 (+ スピン ) こそが 現在の科学の発展を妨げる 最大の要因である。
(Fig.3) 現実の変化に富む世界は 単純な数学上の模型とは違いすぎる。
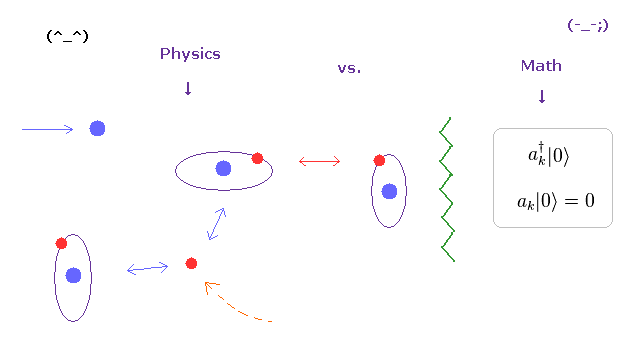
実世界の様々な物理現象、しいては 非常に複雑な 私達人間の高度な生体システムを見て分かるとおり、電子や陽子などの粒子は 実際には 複雑かつ ダイナミックに 動き回っている。
そして それらの粒子が相互作用するタイミングや その時の 微妙な位置関係の違いなどが バライティーに富む 様々な生体機能を決定していると言える。
残念ながら "a†" や "a" などの 単なる抽象的な数学の記号のみでは これらの複雑かつ変化に富む機能を説明することは 不可能である。
(Eq.33)
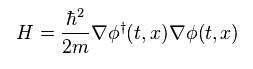
グリーン関数 (= 伝播関数 ) においても、これらの 抽象的な演算子が用いられている。
Eq.33 は 自由粒子のシュレディンガー方程式である。
(Eq.34)
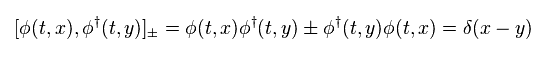
" ± " は 固有関数 (= 演算子 ) における 反交換 と 交換 関係を表す。
シュレディンガー方程式における 固有関数は
(Eq.35)
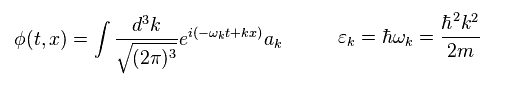
Eq.35 では、"k" は 波数で ħk は 粒子の運動量 p に等しい。
ε は 粒子の ( 運動 ) エネルギー である。
Eq.35 を Eq.34 に代入して、 "a" や "a†" が 次を満たすことが分かる。
(Eq.36)
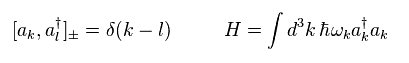
グリーン関数が 時間順序 (= T ) に従って 粒子が ( t', x' ) に生成されて ( t, x ) に消滅することを意味している。
(Eq.37)
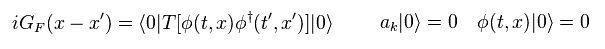
Eq.35 - Eq.37 から、このグリーン関数は 次のヘビサイドの階段関数を用いて
(Eq.38)
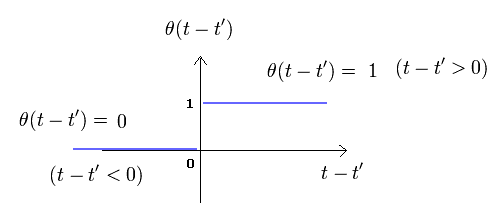
これは 時間順序に用いられる。
Eq.38 の 階段関数 (= θ ) では、 (t-t') が 正のとき、 θ は "1"、 また t-t' が 負のとき、 θ が ゼロになる。
(Eq.39)
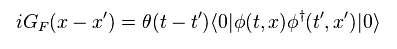
このページに示したように、複素積分を用いて、 階段関数は 次のように表される。
(Eq.40)
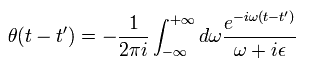
Eq.40 で ε は 無限小である ( ε → 0 )。
Eq.35, Eq.36, Eq.40 を用いて、Eq.39 のグリーン関数は
(Eq.41)
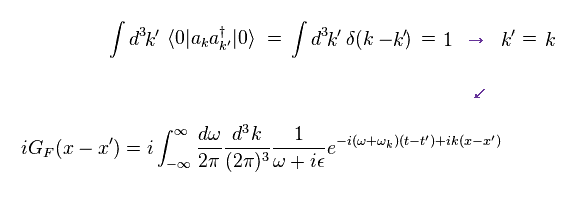
ここでは 次の置き換えをする。
(Eq.42)
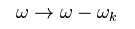
結果的に Eq.41 は、
(Eq.43)
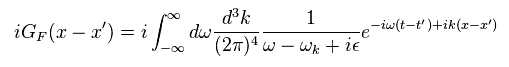
デルタ関数の定義より。
(Eq.44)
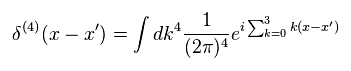
Eq.35、 Eq.43、Eq.44 より、次を得る。
(Eq.45)
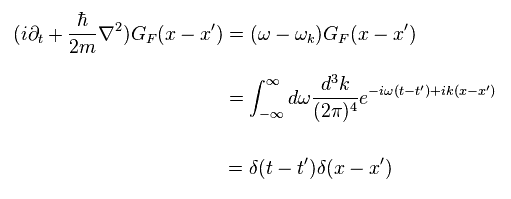
これが シュレディンガーバージョンの グリーン関数 (= 伝播関数 ) である。

2013/9/17 updated This site is link free.