
Top page (correct Bohr model including the two-electron atoms)
Strange "spin" is NOT a real thing
Why they intentionally make physics difficult ?
(Fig.1) Bohr's accelerating electron really radiates ? = " Brainwashing ".

You may often see the explanation such as " Bohr's classical orbit is wrong, because its accelerating electron radiates and loses energy. "
But unfortunately, this explanation is completely wrong.
It uses Poynting vector (= E × H ) as the energy flow.
This Poynting vector is equal to the change of the electric and magnetic energies in the vacuum.
This electric energy in the vacuum (= 1/2εE2 ) means the potential energies needed to gather minus (or plus) small charges to the sphere (= Fig.1 left-below ).
But a single electron is NOT made from smaller charges. ( A single electron is the smallest charge. )
It means the vacuum electric energy in a single electron is NOT energy, and Poynting vector itself is meaningless in this case. See also this page.
So this wrong explanation is a kind of brainwashing about Bohr model, I think.
(Fig.2) Schrodinger equation is one of Bohr-Sommerfeld model.
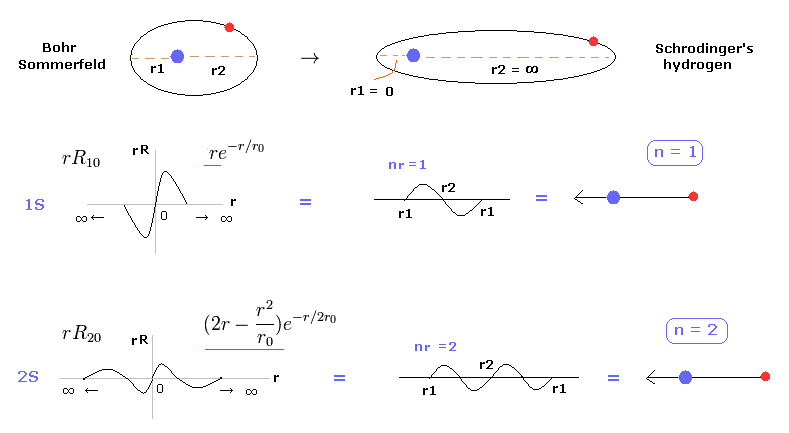
In most textbooks, we often see comments like " Bohr model hydrogen is accidentally consistent with Schrodinger equation and experimental results. "
But it is unnatural that the model, which has nothing to do with truth, can give the correct results.
Actually, we can prove Schrodinger's hydrogen also uses an integer times de Broglie wavelength like Bohr model. See also this page.
And molecular orbital (= MO ) methods often uses various combinations of hydrogen excited states to get correct energies.
As shown in this page, these excited states such as 2p, 3d can be utilized for changing orbital shapes, keeping integers times de Broglie wavelength.
So basically they uses the same principle as Bohr model.
Most important problem is that usual textbooks hide the facts that Bohr-Sommerfeld model gived the completely same fine structure as Dirac equation, as shown in this page
(Fig.3) Tetrahedral structure of carbon-like atoms.
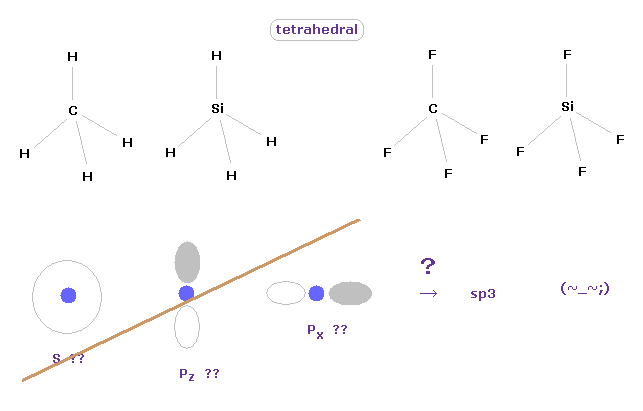
It is said " ab initio " methods in quantum chemistry can give correct values.
But in fact, we need to "artificially" adjust various coefficients for getting various molecular shape.
We can easily imagine that the methane has tetrahedral structure, from the viewpoint of classical mechanics.
If you try to express these tetrahedral ( or octahedral ) structures using quantum mechanics, you need to combine 2s, 2p-x and 2p-y to fit the correct values.
Basis sets used in ab initio methods are artificially determined in each different molecule in STO, GTO, 3-21G.
Choosing which basis sets is most important concepts in quantum chemistry.
(Fig.4) Choosing proper basis set for each atom is important.

It is said that "ab-initio" methods are not based on initial conditions (= function ).
But in the actual calculation, it is just the ideal.
In fact, they prepare different basis function for each atom in ab-initio methods.
For example, in 6-31G, they choose different sized pair of 1s, 2s, and 2p.
( Hydrogen -- 1s, 1s', and carbon -- 2s, 2s', 2p, 2p' ).
These sizes are determined artificially to manipulate scaling factor in advance to fit the results.
And if they cannot get good results, they added other-typed polarized and diffuse functions to them.
In this way, they just artificially choose some proper basis functions, which match the experimental results.
Of course, these basis functions are based on hydrogen energy levels, which completely agrees with Bohr-Sommerfeld hydrogen.
(Fig.5) An electron is spreading as sphere in QM ?

According to quantum mechanics, we cannot designate a single electron in hydrogen atom.
So a single elecctron of quantum mechanics is always spreading as wavefunction.
For example, when a single electron is spreading as sphere, we can consider that electron exists at the center of that sphere, from the viewpoint of potential energy.
If the electron is at the center, it just overlaps positive nucleus (= +e ), and H atom completely becomes neutral.
So that H atom cannot interact with other atoms at all.
So an electron in H atom needs to be localized at some place like Bohr model, when it can interact with other atoms.
(Fig.6) H-H bond = two electrons are avoiding each other.

In hydrogen molecules, two electrons tend to be attracted to other nuclei.
But if we try to express this state using wavefunction sphere, they are repelling each other, as shown in Fig.5 lower figure.
On the other hand, if we use classical orbits, we can express H molecule naturally.
In this natural model, two electrons are avoiding each other (= up and down ), attracted to other positive nuclei, which can form covalent bond.
And as shown in this page, we have succeeded in getting correct experimental values of hydrogen molecule using classical orbits in very easy and natural ways.
In conclusion, we need to use concrete localized ( not spreading ! ) electron in various molecules to express covalent bonds.
(Fig.7) "Mathematical" Schrodinger equation vs. "real" Bohr model.
"Ab-initio" (= first principle ) method is said to be non-emprical.
But in fact, we must choose some proper basis sets artificially in each different molecules.
After choosing basis sets and calculation of usual Hartree-Fock, they combine configuration interaction (= full CI ), MP, and coupled-cluster (= CC ) to them.
As I explain in Fig.5 and Fig.6, electrons must avoid each other to lower energy.
In MO and CI methods, they introduces very complicated determinants to express these repulsive interactions.
Because, in determinants, two electrons cannot be in the same states.
But as shown in Fig.7, due to these very complicated determinants, we cannot apply these useless quantum chemistry to various macro biological interactions.
(Fig.8) Is this useful ?
Even in full CI methods, we cannot get correct binding energy.
They combine MP and CC methods to them.
But these ab initio methods such as MP and CC can give wrong ground state energy, which is lower than experimental results.
So "ab initio" is just to utilize basic hydrogen atom's energy states.
( Of course, these are just equal to Bohr model. Most important difference is they are many-worlds, and Bohr model is not. )
They exaggerate it (= "ab initio" ) too much, I think.
All data of bond length and angles (= experimental values ) in various molecules are gotten from CRC textbook.
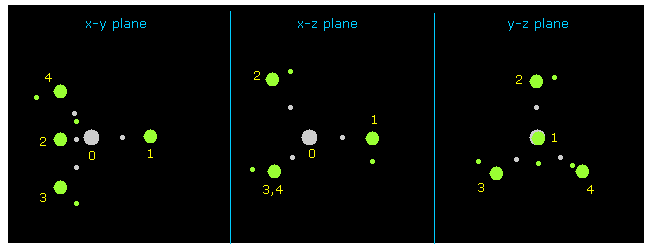
(Fig.9) Methane ( CH4 ).
We use this sample program to compute various molecular interaction.
( Save this text as "orbit.java", and compile it. )
About the detailed manipulation, see this page, first.
C-H bond length is 1.8700 Å (= 18700 MM ), and H-C-H bond angle is 109.45 degree (= tetrahedron ).
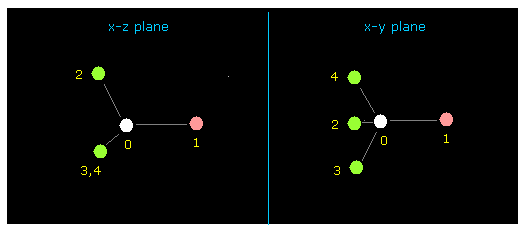
After running program , click "nucleus" button, which displays CH4 picture ( center is atom 0, carbon ) on x-y, x-z and y-z planes.
Hydrogen atoms are expressed as green circle, and central carbon is gray circle.
(Fig.10) Hydrogen atom of CH4

Then input the value of "1" on the designated textbox, and click "electron" button.
If so, electron of atom 1 (= hydrogen in this case ) is displayed on the screen.
You can change the coordinate of this electron by inputting some values ( MM ) into textboxes ( +X, +Y or +Z ) and pressing enter key.
Initial distance (= nuc ) between electron and H nucleus is supposed to 4500 MM (= 0.4500 Å ), which is a little shorter than the Bohr radius (= about 0.5200 Å ).
Because hydrogen electron is attracted to carbon nucleus and its radius is shrunk.
If you input "-5200" (= Bohr radius ) into "+Z (MM)" and press enter key, total potential energy becomes tV = -438.16 eV, which is almost same as the experimental value of -439.35 eV of CH4. See also this page.
(Fig.11) Changing hydrogen electron coordinate.
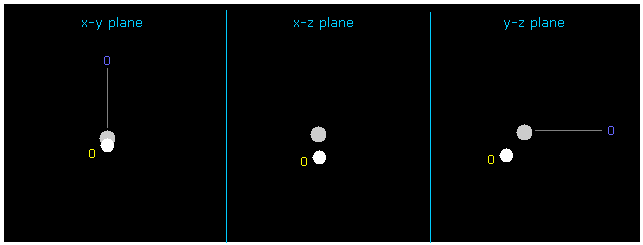
If you input +Y = -1217 and +Z = -3362.0 into textboxes and press enter key, this H electron's position is changed.
In this case, force acting on hydrogen nucleus is just zero ( now 1; FX=3, FY=0, FZ=0 ), and its de Broglie wave is just ave = 1.0000.
But in this case total potential energy is lower (= -480.46 eV ) than the actual value.
Because as I said in this page, we need to consider average distribution of carbon's valence electron, not only in this special state.
Carbon's 4 valence electrons are widely distributed (= 0.6415 Å radius ).
( In this special case, 4 valence electrons of carbon is closest to H nucleus. )
(Fig.12) Four valence electrons of carbon in CH4.
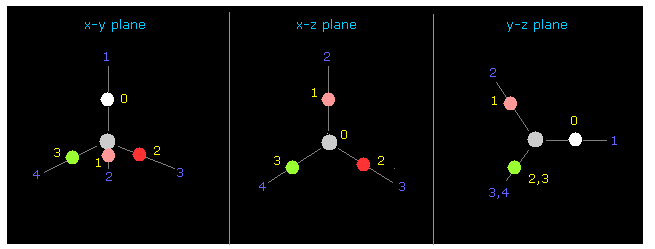
Again we input the value of "-4500" between those values into +Z textbox.
Then input "0" into the designated textbox and click "electron".
If so, four valence electrons of carbon are shown on the screen.
(Fig.13) Force (CF) acting on C electron.
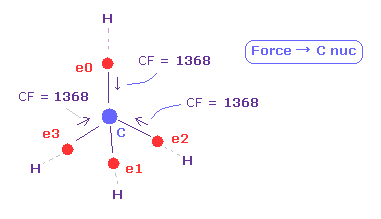
As you see in CF (= force component acting on each electron toward C nucleus ), CF=1368 is proper value.
This CF becomes "1278", when H electron is Bohr radius, and "1455", when H electron's de Broglie waves is just 1.0000.
(Fig.14) Force = 1000.
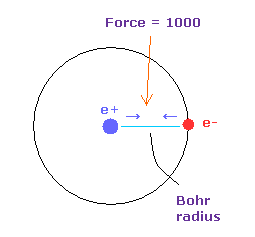
Force unit is shown in Fig.14.
The force between electron and nucleus in H atom ground state is supposed to be "1000".
So when the distance between electron and +e nucleus is Bohr radius, its force becomes 1000.
For example the force of 1468 is 1.468 times that in H atom ground state.
| C-H bond length | CF ( Z = -0.4500 Å ) | CF ( Bohr radi ) | CF ( wave = 1.0 ) | CF ( other ele 1-3 ) |
|---|---|---|---|---|
| 0.9000 Å | -1383 | -1519 | -- | +1382 |
| 0.9500 Å | -121 | -250 | -- | +1377 |
| 1.0000 Å | +636 | +520 | +816 | +1374 |
| 1.0870 Å | +1368 | +1278 | +1455 | +1368 |
| 1.1500 Å | +1660 | +1587 | +1704 | +1367 |
Table 1 shows how force (= CF ) acting on carbon valence electron 0 changes depending on C-H bond length.
C-H bond length can be changed freely when the screen is Fig.9 (= atomic picture ).
Input some value into "+X (MM)" textbox of atom 1, and press enter key.
When C-H bond length is 1.0870 Å (= experimental value ), force CF is about 1400, which is good.
CF left, center, right mean forces when ele 0's relative coordinate is Z=-0.4500 Å, Z=-0.5200 Å (= Bohr radius ), and when de Broglie waves is 1.000, respectively.
(Fig.15) Carbon electron (= e0 ) is attracted to H, instead of C !?
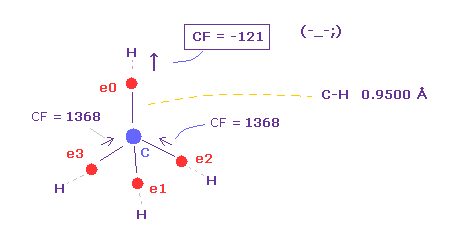
As you see in Table 1, when C-H bond length is shorter (= 0.9500 Å ), force toward C nucleus becomes negative ( CF = -121 ).
This means carbon valence electron e0 is attracted to hydrogen nucleus instead of C nucleus !
So in this case, electrons and H nucleus become unstable !
When C-H length is short like 0.9500 Å, de Broglie wave cannot be 1.000 to stop H nucleus.
Also in C-H = 1.0000 Å, CF = 636 is too small.
( As I said in Fig.14, even the force in simple hydrogen atom is as much as "1000". )
In conclusion, this stability of valence electrons and nuclei determines C-H bond length of methane, as I said in this page.
(Fig.16) Fluoromethane (= F-CH3 ) molecule.
After running the program, input "0" to choose methane-like molecule, and then input "1" to choose F-CH3.
About the detailed methods, see also this page.
(Fig.17) Fluoromethane (= F-CH3 ).
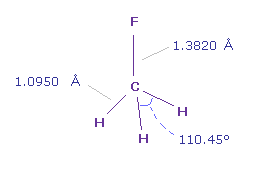
In fluoromethane, C-F bond length is 1.3820 Å and C-H bond length is 1.0950 Å.
On the screen, fluorine (= F ) atom is on x axis, and "nuc" in the textboxes means lengths between each atom and 0 (= C ) atom.
Actual H-F-H angle is 110.45 degree, but it's almost 109.45 degree of tetrahedron.
So here we think about usual 109.45 degree.
( Of course, you can change these coordinates, if you change each atomic coordinate. )
(Fig.18) Rotate fluorine by 90 degree on x-y plane to avoid repulsive force.
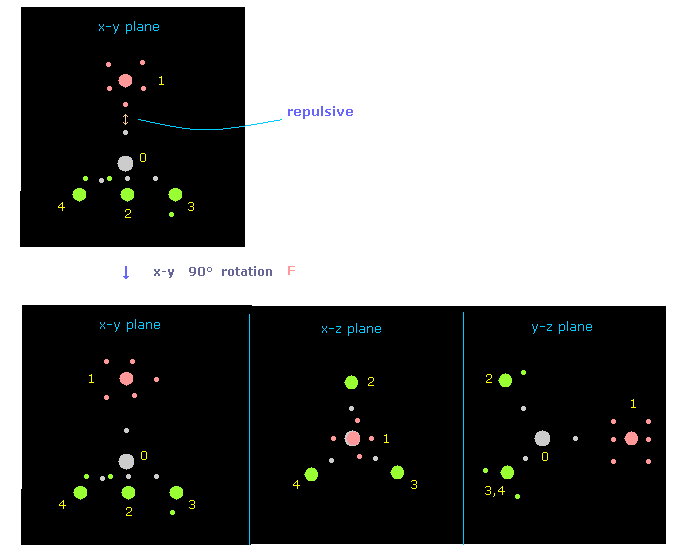
Just after running program, the pointed fluorine valence electron and carbon's electron are very close to each other.
So to avoid strong repulsive force between them, rotate fluorine by 90 degree on x-y plane, as I explain in this page.
In Fig.18, atom 1 (= F ) is turned from x-axis to y-axis, by clicking "direction" button ( "1" is inputted next to it ).
(Fig.19) Force acting on C nucleus is "balanced".
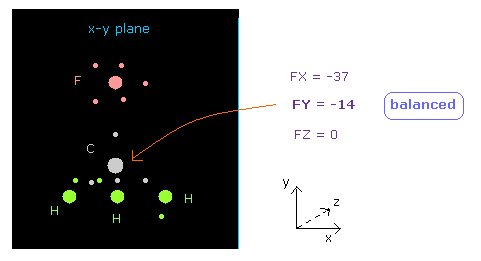
See "now 0" line below in nucleus picture, which means forces acting on atom 0 (= carbon ).
( "now" means the present chosen atom. )
You can see FY = -14, which is almost zero.
So force acting on central carbon nucleus is just balanced among one F and 3× H atoms, in this case.
If you input "12000" on the textbox of "+Y (MM)" in "atom 1" line, and press enter key, the bond length F-C changes to 12000 MM (= 1.2000 Å ).
In this case, force acting on carbon becomes ( FY = -125 ), due to stronger repulsive force by F nucleus.
So the bond length of 13820 MM (= 1.3820 Å ) is determined for their equilbrium.
(Fig.20) Force acting on four valence electrons are "balanced".

Again input "13820" on the textbox of "+Y (MM)" in "atom 1" line, and press enter key.
Next input "0" next to "electron" button, anc click "electron" button.
Then four valence electrons ( 0-3 ) of carbon atom is displayed.
( Blue number around them represents surrounding atomic number. )
See force "CF" of each electron, which means force component toward C nucleus acting on each valence electron.
( We can use this CF for judging force balance of 4 surrounding atoms. )
As shown in Fig.20, when F-C and H-C length is 1.3820 Å and 1.0950 Å, these forces are almost equal to each other.
CF = 1764 at F side, and CF = 1417 at H side.
(Fig.21) Force balance is broken.

Again click "nucleus" button, move to atomic picture, and change +Y coordinate to "12000" from "13820".
This means F-C bond length is shorter ( 1.3820 Å → 1.2000 Å ).
Then click "electron" button ( neighboring text is "0" ), and see force CF of carbon valence electrons again.
As you see in Fig.21, when F-C length is shorter (= 1.2000 Å ), carbon valence electron "0" is too attracted to fluorine nucleus.
So CF = 356 is too weak, comparing other CF = 1425.
( Of course, fluorine nucleus is also attracted to this electron 0 too much in this case. )
This means these particles become unstable in the same mechanism as CH4 above.
| F-C bond length | Force on e0 | Force on e1 | Force on e2 | Force on e3 | FY on C nucleus |
|---|---|---|---|---|---|
| 1.1500 Å | -644 | +1425 | +1428 | +1428 | -173 |
| 1.2000 Å | +356 | +1423 | +1425 | +1427 | -125 |
| 1.2500 Å | +985 | +1423 | +1425 | +1427 | -125 |
| 1.3820 Å | +1764 | +1417 | +1417 | +1422 | -14 |
| 1.4500 Å | +1935 | +1415 | +1415 | +1420 | +12 |
As you see in Table 2, when the F-C bond length becomes shoter than the experimental value (= 1.3820 Å ), carbon's valence electron tends to be too much attracted to fluorine, and becomes unstable.
When F-C is 1.3820 Å. all four forces in e0-e3 are almost equal to each other.
This phenomenon is just the same as methane, and its factor determines the bond length.
And the force acting on C nucleus is balanced ( FY on C is alomost zero ), when F-C length is 1.3820 Å.
Total ionization energies are carbon 1-4th (= 148.024 eV ), hydrogen (= 13.606 eV ), fluorine 1-7th (= 658.83 eV ).
See also this page.
And considering C-H bond energy ( 411 kJ/mol = 4.26 eV ) and C-F bond energy ( 485 kJ/mol = 5.02 eV ), the experimental value of total energy becomes -865.457 eV.
Using Virial theorem, total potential energy is 2 × -865.457 = -1730.91 eV.
This experimental value is almost same as computed value (= -1731.91 eV ) using the program above.
(Fig.21') Force acting on fluorine.
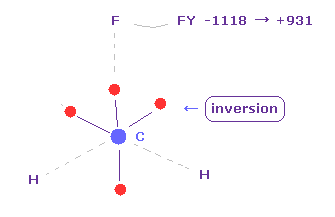
When C electron is closest to fluorine, force acting on flurine becomes FY = -1118.
This value looks big, but considering F big positive nucleus and short distance between F electron and its nucleus, this force can be easily canceled out by moving some of F valence electrons a little.
( Actually, some of F valence electrons are repelled by C electron. Try it. )
C electrons are moving periodically around C nucleus.
Click "electron" button ( "0" is inputted ), and display C electrons.
And then click "inversion" button.
( All four C electrons move to the opposite positions of nucleus. )
If so, F nucleus are repelled by C nucleus after C electron goes away.
Sum of them (= -1118 + 931 ) is almost zero and balanced.
(Fig.22) Force acting on C electrons.
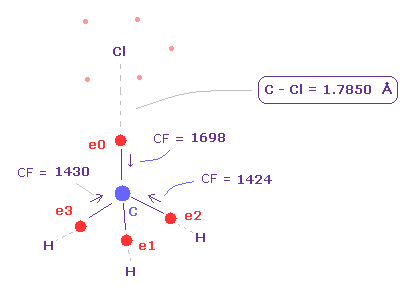
After runngin the program, choose "methane-like = 0" and "Cl-CH3 = 2".
In the same way as F-CH3 above, we rotate Cl atom 90 degree.
As shown in Fig.22, when the C-Cl length is the experimental value of 1.7850 Å, force acting on carbon valence electrons are well-balanced.
( e0, e1, e2, e3 = 1698, 1426, 1424, 1430 ).
| Cl-C bond length | Force on e0 | Force on e1 | Force on e2 | Force on e3 |
|---|---|---|---|---|
| 1.5500 Å | +895 | +1449 | +1447 | +1451 |
| 1.6000 Å | +1145 | +1443 | +1441 | +1446 |
| 1.6500 Å | +1343 | +1438 | +1436 | +1441 |
| 1.7850 Å | +1698 | +1426 | +1424 | +1430 |
| 1.8500 Å | +1806 | +1421 | +1419 | +1426 |
As shown in Table 3, when Cl-C bond length is experimental value (= 1.7850 Å ), forces acting on carbon valence electrons are well-balanced.
Like other methane-like molecule, when Cl-C length is shorter, C valence electron e0 tends to be too much attracted to Cl nucleus, and becomes unstable.
--------------------------------------------------
Here we investigate the influences on carbon's electron "ele 0" in various carbon bonds, and some common mechanism is working.
After running this program of this page, choose "C" (= carbon ) as "A atom".
And choose various atoms as "B atom".
(Fig.C-1) Comparison of forces acting on C electron.
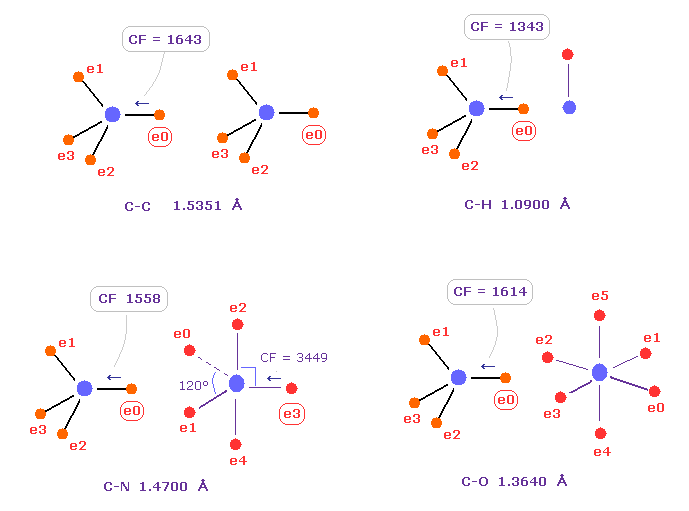
Fig.C-1 shows forces acting on carbon electron "e0" in C-C, C-H, C-N and C-O single bonds.
Considering carbon can keep tetrahedral structure in various bonds, it is natural forces acting on C electron are almost equal to each other.
Actually, these forces (= CF ) are 1643, 1343, 1558, 1614 in different C-C, C-H, C-N, C-O bonds, respectively.
( These bond lengths are average experimental values. C-O single bond is from acetic acid. )
| molecular bond | bond length | Force on e0 |
|---|---|---|
| C - H | 1.0900 Å | CF = 1343 |
| C - C | 1.5351 Å | CF = 1643 |
| C - N | 1.4700 Å | CF = 1558 |
| C - O | 1.3640 Å | CF = 1614 |
| C - F | 1.3500 Å | CF = 1605 |
| C - Si | 1.8500 Å | CF = 1602 |
| C - P | 1.8400 Å | CF = 1584 |
| C - S | 1.8200 Å | CF = 1708 |
| C - Cl | 1.7700 Å | CF = 1626 |
Table C shows forces (= CF ) acting on carbon electron "ele 0" in various bonds.
Surprisingly, in different bonds, these forces (= CF ) become almost same !
This means common mechanism is working, and carbon's tetrahedral structure is kept in various bonds.
-------------------------------------------------
Total ionization energies are carbon 1-4th (= 148.024 eV ), hydrogen (= 13.606 eV ), chlorine 1-7th (= 408.88 eV ).
See also this page.
And considering C-H bond energy ( 411 kJ/mol = 4.26 eV ) and C-Cl bond energy ( 327 kJ/mol = 3.39 eV ), the experimental value of total energy becomes -613.89 eV.
Using Virial theorem, total potential energy is 2 × -613.89 = -1227.78 eV.
This experimental value is almost same as computed value (= -1230.46 eV ) using the program above.
(Fig.23) Force acting on carbon nucleus.
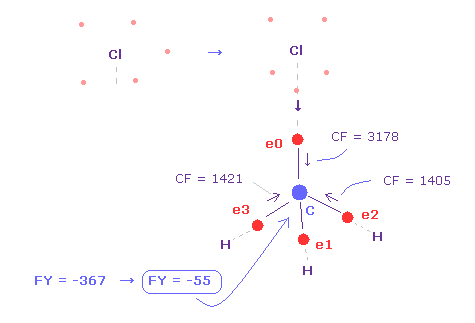
The problem is valence electrons of chlorine is widely distributed due to "3" de Broglie wavelength.
So as it is, repulsive force by Cl nucleus is too strong, because it is exposed.
Actually, force acting on C nucleus is FY = -367, which is bigger than that of F ( FY = -14 in Fig.19 ).
Due to widely spreading electrons, these electrons are not so strongly bound to Cl nucleus.
( CF=2900 in chlorine and CF = 9000 in fluorine. )
So even when C valence electron comes close to Cl, Cl electron tends to point toward C nucleus ( Fig.23 ).
In this case, force acting on C nucleus becomes FY = -55, which is almost balanced.
( Of course, even in this case, these electrons are avoiding each other as possible. )
| Cl-C bond length | Force on e0 | FY on C nuc-1 | FY on C nuc-2 |
|---|---|---|---|
| 1.5500 Å | +13778 | -662 | +113 |
| 1.6000 Å | +8018 | -581 | +49 |
| 1.6500 Å | +5508 | -512 | +5 |
| 1.7850 Å | +3178 | -367 | -55 |
| 1.8500 Å | +2793 | +-313 | -66 |
As shown in Fig.23, when Cl-C bond length is experimental value of 1.7850 Å, force acting on carbon nucleus is almost balanced ( FY = -55 ), when one of Cl valence electron points toward C nucleus. (= FY on C nuc-2. )
In this case, due to the repulsive force between close electrons, CF of e0 becomes bigger (= 3178 ).
When C electrons are opposite, this CF becomes about 2700.
Comparing with 2700, the value of 3178 is acceptable one.
But when Cl-C length is shorter, repulsive forces between C and Cl becomes unrealistically stronger.
( As a result, CF on e0 becomes much bigger +5508, +8018, +13778... ).
So Cl electron cannot point toward C nucleus, when C electron is close to Cl, in these bond lengths.
As a result, Cl tends to be always like Fig.22, and force FY acting on C nucleus is bigger ( see FY on C nuc-1 ), and becomes unstable, when Cl-C length is shorter than experimental value.
(Fig.24) Fluoroform (= HCF3 ) and chloroform (= HCCl3 ) .
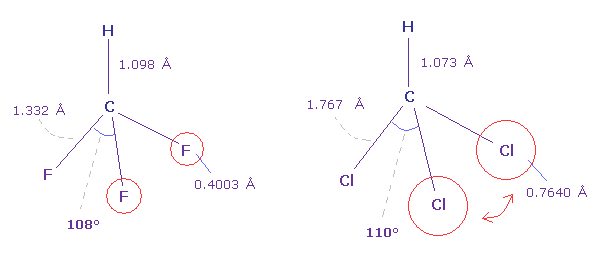
As shown in Fig.24, F-C-F angle (= 108.5 degree ) of fluoroform is a little smaller than basic tetrahedron (= 109.5 degree ).
Because the valence electrons around C nucleus tend to be attracted toward F, and electron density of F sides becomes lower .
But Cl-C-Cl angle of chloroform is a little bigger (= 110.4 degree ), though Cl has stronger electronegativity than carbon.
Because seven valence electrons of chlorine spread over larger area (= 0.7640 angstrom ) than fluorine (= 0.4003 angstrom ).
Due to electron's wide distribution, positive chlorine nucleus is exposed, and exerts stronger repulstive force.
Compare forces FY against C nucleus in Table 4 (= Cl ) and Table 2 (= F ).
(Fig.25) Water ( H2O ) structure.
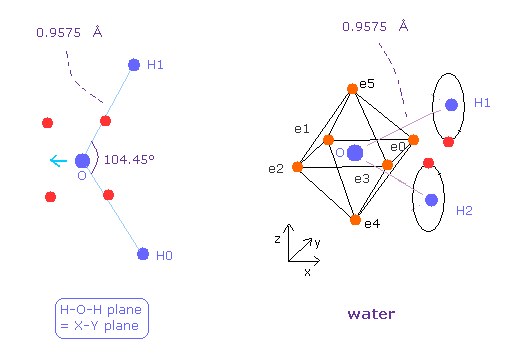
Next we think about water (= H2O ).
After running the program, choose H2O-like (= 1 ), and then H2O (= 0 ).
The oxygen of H2O is asymmetric unlike carbon of methane.
Due to positive nuclei of two hydrogen, oxygen's electrons bend toward H nuclei.
( Bond length and angles in Fig.25 are experimental values. )
(Fig.26) How much do oxygen's electrons bend ?

As shown in this page, for upper and lower electrons (= e4, e5 ) to bend toward H nuclei, e1 an e2 electrons need to be attracted outward.
( e4 and e5 electrons can strongly pull O nucleus toward H nuclei by a little movement. )
So H-O-H angle needs to be a little wider than 90 degree (= angle of octahedron ).
( In this page, electron number of Fig.25 is used. )
(Fig.27) Adjusting O position.
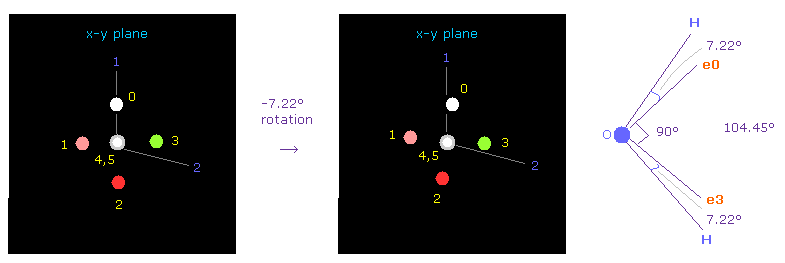
In this program, electron 0 of oxygen is automatically turned toward atom 1 at initialization.
We want to turn these electrons to the symmetrical positions with respect to both atoms 1 and 2.
So click "electron" button ( input "0" next to it ) to display oxygen's electrons.
And then rotate them by -7.22 degree on x-y plane to make it symmetrical with respect to two hydrogen.
( Input "-7.22" on the designated textbox, and click "x-y ang" button )
(Fig.28) Repulsive force between O-H.
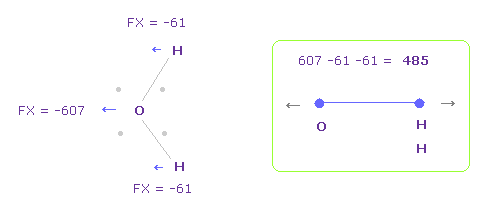
To know how much oxygen valence electrons bend, we investigate total amount of repulsive FX.
In Fig.28, O is repelled ( FX = -607 ) to the left, and two H are attracted to oxygen ( 61 × 2 = 122 ).
So total repulsive force becomes 485.
The average single O-H bond energy of the water is 9.6066 eV (=926.9 kJ/mol) / 2 = 4.8033 eV.
So the total energy of H2O is -433.103 (O) - 2 × 13.606 (H) - 9.6066 (bond energy) = -469.92 eV.
Here 433.103 eV is total ionization energy of oxygen 6 valence electrons.
According to Virial theorem, experimental value of total V is -939.84 eV (= 2 × E ).
In Fig.28, total V becomes -935.14 eV, which is almost same.
(Fig.29) Repulsive force betwee O-H, part II.
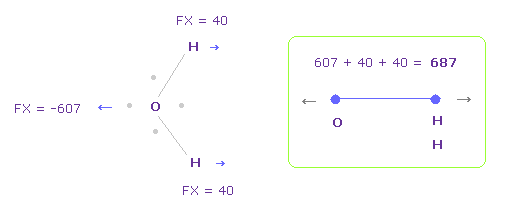
In Fig.28, oxygen valence electrons are closest to H nuclei.
Considering oxygen electrons are orbiting, we think about Fig.29 case, too.
And we take their average.
To get Fig.29, rotate oxygen electron by -45 degree on x-y plane from Fig.28
In this case, total repulsive force between O-H becomes 687.
(Fig.30) Average force.
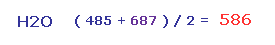
So the average repulsive force of Fig.28 and Fig.29 is ( 485 + 687 ) / 2 = 586.
This value needs to be cancelled out mainly by bending of oxygen.
(Fig.31) Adjusting Oxygen position in OF2.
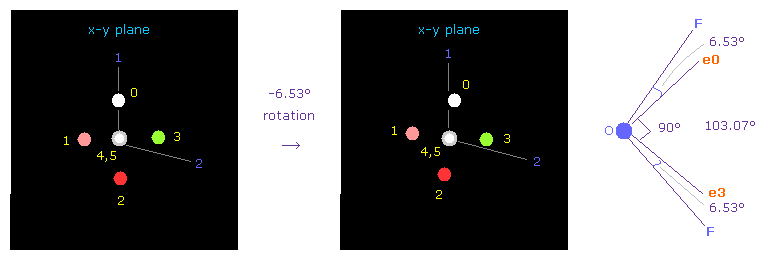
Next we choose OF2 molecule (= oxygen + two fluorines ).
After running the program, input "1" (= H2O like ), and then input "1" (= OF2 ).
F-O-F bond angle is 103.07 degree, so in oxygen electron's screen, rotate it by -6.53 degree on x-y plane to get symmetric position.
(Fig.32) Rotating fluorine by 90 degree.
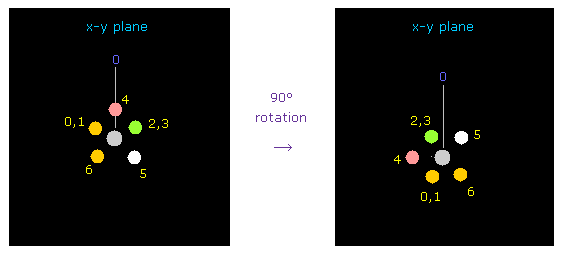
Considering repulsive force between carbon and fluorine electrons, we rotate two fluorines by 90 degree on x-y plane.
Click "electron" button ( after input "1" or "2" on the textbox ), and input "90", and click "x-y ang" button.
As a result, we can get Fig.33 state.
Click "nucleus" button ( after input "0" ), and confirm it.
(Fig.33) Repulsive force between O-F in OF2.
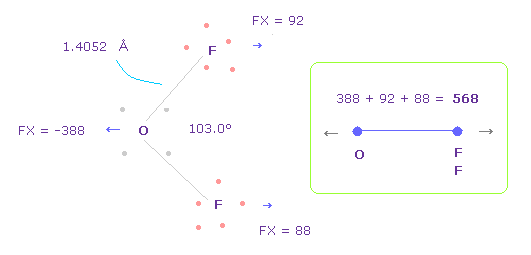
The bond length and angles in Fig.33 are experimental values.
As I said in H2O, to know how much oxygen valence electrons bend, we investigate total amount of repulsive FX in OF2, too
In Fig.33, O is repelled ( FX = -388 ) to the left, and two F are also repelled by oxygen ( 92 + 88 = 180 ).
So total repulsive force becomes 568.
Single O-F bond energy is 1.969 eV (=190 kJ/mol ), which is small.
So the total energy of OF2 is -433.103 (O) - 2 × 658.83 (F) - 1.969 × 2 = -1754.70 eV.
Here 658.83 eV is total ionization energy of fluorine 7 valence electrons.
According to Virial theorem, experimental value of total V is -3509.4 eV (= 2 × E ).
In Fig.28, total V becomes -3500.63 eV, which is a little higher.
( We need to adjust their electron's positions a little. )
Actually O-F and F-F bond is very unstable due to their repulsive force.
So fluorine cannot be alone in nature, and O-F bond length (= 1.4025 Å ) is longer than C-F bond (= 1.3820 Å )
(Fig.34) Repulsive force between O-F, part II.
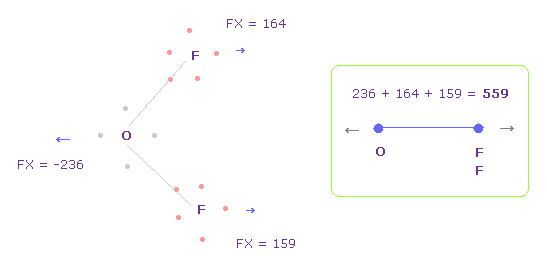
In Fig.33, oxygen valence electrons are closest to F nuclei.
Considering oxygen electrons are orbiting, we think about Fig.34 case, too.
To get Fig.34, rotate oxygen electron by -45 degree on x-y plane from Fig.33.
And then click "electron" button ( after input "1" or "2" ), and rotate two F by -90 degree on x-y plane to return their original states.
In this case, total repulsive force between O-F becomes 559.
(Fig.35) Average force.
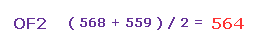
So the average repulsive force of Fig.33 and Fig.34 is ( 568 + 559 ) / 2 = 563.
This value needs to be cancelled out mainly by bending of oxygen.
And "oxygen bending" is almost same in O-H (= 586 in Fig.30 ) and O-F (= 563 in Fig.35 ).
Basically, 1/2 of each total repulsive force is oxygen bending.
( 1/4 of it is H or F bending, respectively. )
This indicates that some common mechanism is working both in H2O and OF2.
(Fig.36) Adjusting Oxygen position in OCl2.
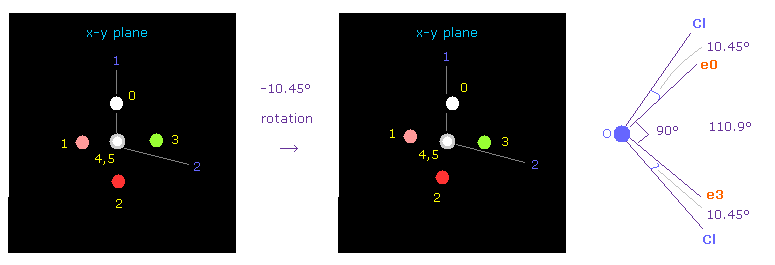
Next we choose OCl2 molecule (= oxygen + two chlorines ).
After running the program, input "1" (= H2O like ), and then input "2" (= OCl2 ).
Cl-O-Cl bond angle is 110.9 degree, so in oxygen electron's screen, rotate it by -10.45 degree on x-y plane to get symmetric position.
As I said in Fig.23, chlorine's valence electrons are widely distributed, so Cl nucleus is exposed.
Considering their weak binging and long O-Cl bond length, we suppose that one of Cl electrons almost always tends to point to O nucleus.
(Fig.37) Repulsive force between O-Cl in OCl2.
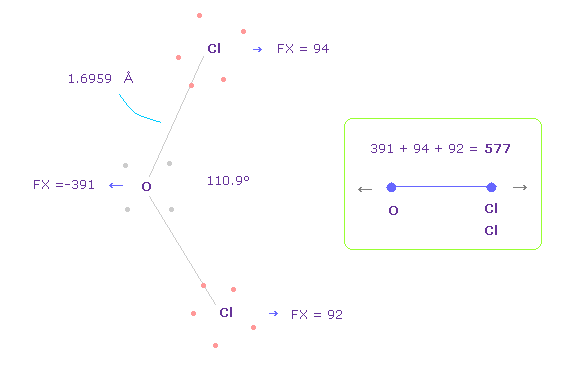
The bond length and angles in Fig.37 are experimental values.
As I said in H2O, to know how much oxygen valence electrons bend, we investigate total amount of repulsive FX in OCl2, too
In Fig.37, O is repelled ( FX = -391 ) to the left, and two Cl are also repelled by oxygen ( 94 + 92 = 186 ).
So total repulsive force becomes 577.
(Fig.38) Repulsive force between O-Cl, part II.
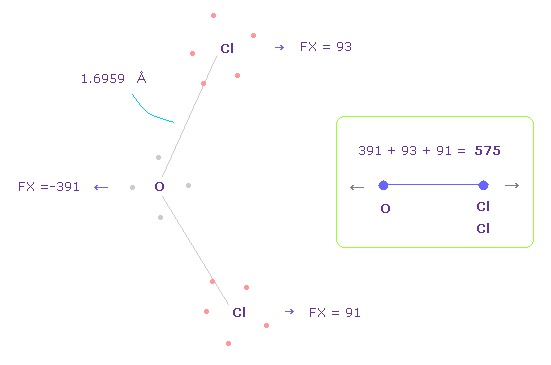
In Fig.37, oxygen valence electrons are closest to Cl nuclei.
Considering oxygen electrons are orbiting, we think about Fig.38 case, too.
To get Fig.38, rotate oxygen electron by -45 degree on x-y plane from Fig.37.
In this case, total repulsive force between O-Cl becomes 575.
(Fig.39) Average force.
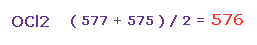
So the average repulsive force of Fig.37 and Fig.38 is ( 577 + 575 ) / 2 = 576.
This value needs to be cancelled out mainly by bending of oxygen.
And "oxygen bending" is almost same as O-H (= 586 in Fig.30 ) and O-F (= 563 in Fig.35 ).
So we can find the common principle in H2O, OF2, and OCl2 from the viewpoint of oxygen bending.
( 586, 563, 576, in H2O, OF2, OCl2, respectively. )
Repulsive force between two chlorines are strongest. ( Compare FY on each Cl and F ).
So Cl-O-Cl bond angle is biggest in them.
| O-H bond length | Repulsive-1 | Repulsive-2 | Average force |
|---|---|---|---|
| 0.8500 Å | 598 | 1024 | 811 |
| 0.9000 Å | 541 | 845 | 693 |
| 0.9575 Å | 485 | 687 | 586 |
| 1.0000 Å | 441 | 593 | 517 |
We investigate the relation between O-H bond length and repulsive force.
To change O-H bond length, use "direction" button, and turn 1 or 2 atom toward y axis, and change their Y coordinate to some value, which becomes bond length.
As shown in Table 5, when O-H bond length of water is experimental value of 0.9757 Å, repulsive force of 586 is almost same as 563 and 576 in OF2 and OCl2.
This means the common mechanism is working in oxygen bending in various molecules.
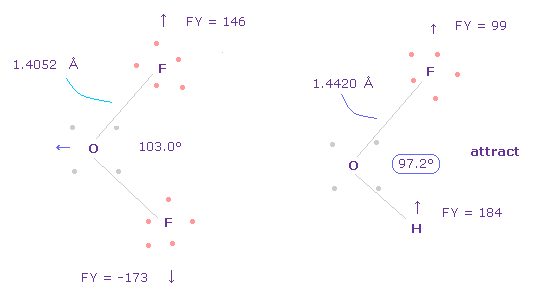
(Fig.40) Adjusting Oxygen position in OFH.
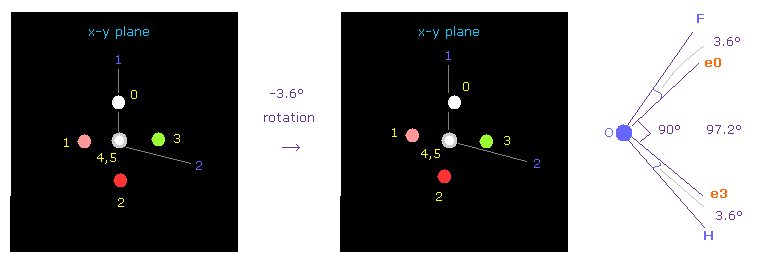
Next we choose OFH molecule (= oxygen + fluorine + hydrogen ).
After running the program, input "1" (= H2O like ), and then input "3" (= OF2 ).
F-O-H bond angle is 97.2 degree, so in oxygen electron's screen, rotate it by -3.6 degree on x-y plane to get symmetric position.
(Fig.41) Rotating fluorine by -90 degree.
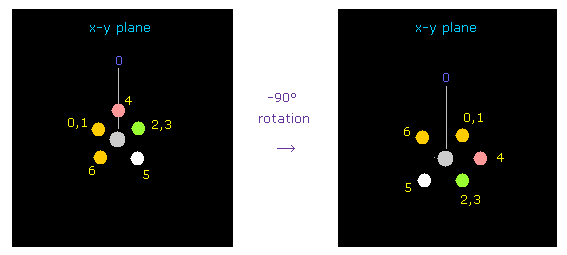
Considering repulsive force between carbon and fluorine electrons, we rotate fluorines by -90 degree on x-y plane.
Click "electron" button ( after input "1" on the textbox ), and input "-90", and click "x-y ang" button.
( Here -90 degree rotation makes oxygen nucleus more stable than 90 degree. )
As a result, we can get Fig.42 state.
Click "nucleus" button ( after input "0" ), and confirm it.
(Fig.42) Repulsive force between O-F,H in OFH.
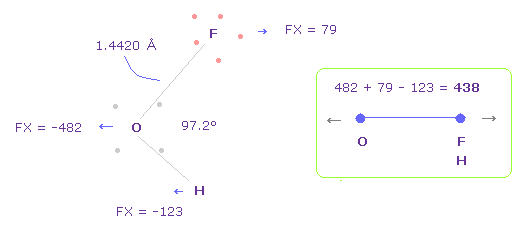
The bond length and angles in Fig.42 are experimental values.
As I said in H2O, to know how much oxygen valence electrons bend, we investigate total amount of repulsive FX in OFH, too
In Fig.42, O is repelled ( FX = -482 ) to the left, and F are also repelled by oxygen ( FX = 79 ).
H are attracted to oxygen ( FX = -123 )
So total repulsive force becomes 482 + 79 - 123 = 438.
Single O-F and O-H bond energies are 1.969 eV (=190 kJ/mol ) and 4.75 eV (= 459 kj/mol) .
So the total energy of OFH is -433.103 (O) - 658.83 (F) - 1.969 - 4.75 = -1098.65 eV.
Here 658.83 eV is total ionization energy of fluorine 7 valence electrons.
According to Virial theorem, experimental value of total V is -2197.30 eV (= 2 × E ).
In Fig.42, total V becomes -2217.88 eV, which is a little lower.
(Fig.43) F and H are attracting each other.
Because hydrogen and fluorine tend to attract each other.
So this F-H bond energy also needs to be considered.
And two fluorines repel each other.
Actually, F-O-F angle is wider than F-O-H angle, and if you see forces FY, you can understand this fact.
(Fig.44) Repulsive force between O-F,H, part II.
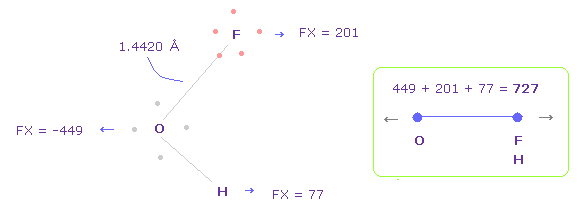
In Fig.42, oxygen valence electrons are closest to F nuclei.
Considering oxygen electrons are orbiting, we think about Fig.44 case, too.
To get Fig.44, rotate oxygen electron by -45 degree on x-y plane from Fig.42.
And then click "electron" button ( after input "1" ), and rotate two F by 90 degree on x-y plane to return its original state.
In this case, total repulsive force between O-F,H becomes 727.
(Fig.45) Average force.
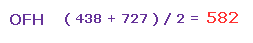
So the average repulsive force of Fig.42 and Fig.44 is ( 438 + 727 ) / 2 = 582.
This value needs to be cancelled out mainly by bending of oxygen.
And this value is reasonable, because it's between H2O (= 586 in Fig.30 ) and OF2 (= 563 in Fig.35 ).
| Molecule : | H2O | OF2 | OCl2 | OFH |
|---|---|---|---|---|
| Repulsive force: | 586 | 564 | 576 | 582 |
As a result, we can know the common mechanism is working in various H2O-like molecules such as H2O, OF2, OCl2, and OFH, with respect to total repulsive force (= oxygen bending ), from Table 6.
Try OClH case, too.
The point is exposed Cl nucleus has strong repulsive force, and one of Cl electron always tends to point to oxygen nucleus due to long O-Cl length.
(Fig.46) Formaldehyde ( O=CH2 ).
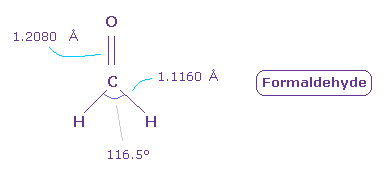
Next we think about formaldehyde ( O=CH2 ).
The double bond length of C=O is 1.2080 Å, and H-C bond is 1.1160 Å
H-C-H angle is 116.5 degree.
After running the program, input "2" (= formaldehyde like ), and then input "0" ( O=CH2 ), and press enter key.
(Fig.47) Rotation of C by -54.73 degree on y-z plane.
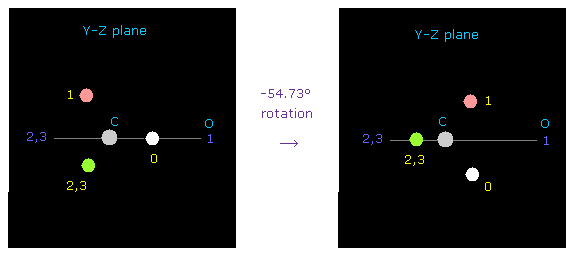
At initialization, carbon valence electron "e0" points toward atom 1 (= oxygen ).
To express double bonds, rotate carbon electrons by -54.73 degree on y-z plane.
( Input "0", click "electron" button, input -54.73, and click "y-z ang" button. )
(Fig.48) Rotation of O by -45 degree on x-y plane.

Also at oxygen side, rotate oxygen by -45 degree on x-y plane to express double bonds.
( Input "1", click "electron" button, input -45, and click "x-y ang" button. )
(Fig.49) Forces on C nucleus.
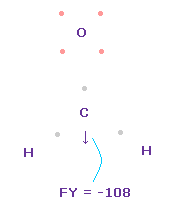
In this state, total forces acting on carbon nucleus ( atom 0 ) becomes FY = -108, which is almost zero.
In Fig.49, H-O-H angle is the experimental value of 116.5 degree, but corresponding carbon electron's e2-C-e3 angle remains to be original 109.45 degree.
(Fig.50) Widening carbon electron's angle from 109.45 to 116.5 degree.
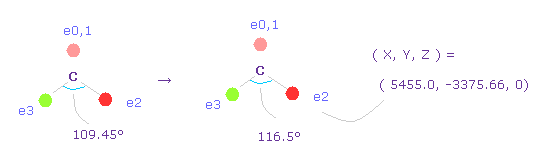
Considering attractive force of two hydrogen nuclei, we widen the angle of carbon's valence electrons from 109.45 to 116.5 degree.
Input "0", click "electron" button, and input the coordinate of ( 5455.0, -3375.66, 0 ) into ele 2 textbox.
And input ( -5455.0, -3375.66, 0 ) into ele 3, and press enter key.
(Fig.51) Forces on C nucleus.
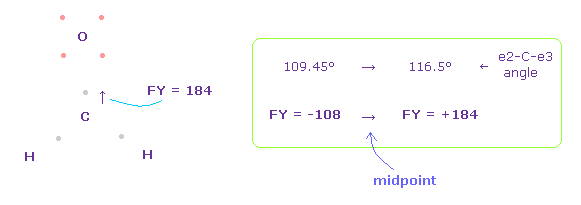
In this case, force acting on C nucleus becomes FY = +184.
As a result, two electrons of carbon are a little attracted to two H nuclei, and the angle of e2-C-e3 becomes between original 109.45 and 116.5 degree to make C nucleus stable.
So these classical orbits can explain nuclear stability also in formaldehyde.
(Fig.52) Forces on oxygen nucleus.
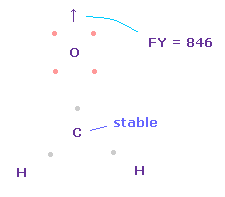
Total forces acting on carbon can be almost zero, when its electron's angle becomes a little wider, attracted to two H nuclei.
The problem is that the repulsive force of carbon nucleus against oxygen is too strong as it is ( FY = 846 ).
(Fig.53) Carbon's electron rotation.
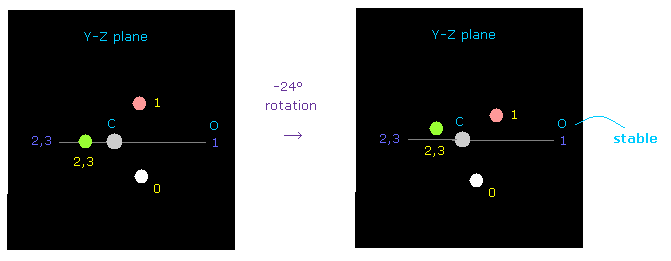
But when you rotate carbon's valence electrons a little by -24 degree on y-z plane, repulsive force against oxygen nucleus can be easily cancelled out.
Oxygen's electronegativity is stronger than carbon, and their electron's rotating periods are different.
Considering these facts, one of carbon electrons often comes close to oxygen even in C=O double bond.
( Probably, the actual rotation angle is between 0 to -24 degree, considering oxygen bending. )
(Fig.54) O=CF2 molecule.
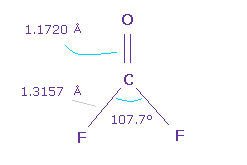
Next we think about O=CF2 molecule.
The double bond length of C=O is 1.1720 Å, and F-C bond is 1.3157 Å
H-C-H angle is 107.7 degree, which is smaler.
Because due to strong electronegativity of F, carbon's electrons are attracted to F, and electron density at F side is decreased.
After running the program, input "2" (= formaldehyde like ), and then input "1" ( O=CF2 ), and press enter key.
(Fig.55) Rotation of C by -54.73 degree on y-z plane.

Like formaldehyde case, to express double bonds, rotate carbon electrons by -54.73 degree on y-z plane.
( Input "0", click "electron" button, input -54.73, and click "y-z ang" button. )
(Fig.56) Rotation of O by -45 degree on x-y plane.

Also at oxygen side, totate oxygen by -45 degree on x-y plane to express double bonds.
( Input "1", click "electron" button, input -45, and click "x-y" button. )
(Fig.57) Rotating fluorine by 90 degree.

Considering repulsive force between carbon and fluorine electrons, we rotate two fluorines by 90 degree on x-y plane.
Click "electron" button ( after input "2" or "3" on the textbox ), and input "90", and click "x-y ang" button.
(Fig.58) Forces on C nucleus.
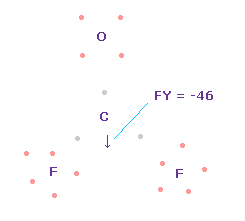
In this state, total forces acting on carbon nucleus ( atom 0 ) becomes FY = -46, which is almost zero.
In Fig.58, H-O-H angle is the experimental value of 107.7 degree, but corresponding carbon electron's e2-C-e3 angle remains to be original 109.45 degree.
(Fig.59) Narrowing carbon electron's angle from 109.45 to 107.7 degree.
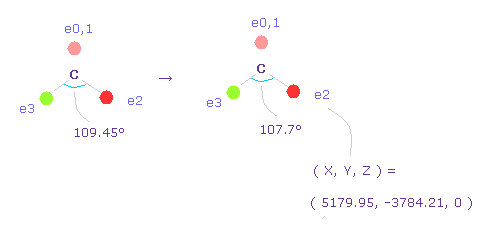
Considering attractive force of two fluorine nuclei, we narrow the angles of carbon's valence electrons from 109.45 to 107.7 degree.
Input "0", click "electron" button, and input the coordinate of ( 5179.95, -3784.21, 0 ) into ele 2 textbox.
And input ( -5179.95, -3784.21, 0 ) into ele 3, and press enter key.
(Fig.60) Forces acting on C nucleus.
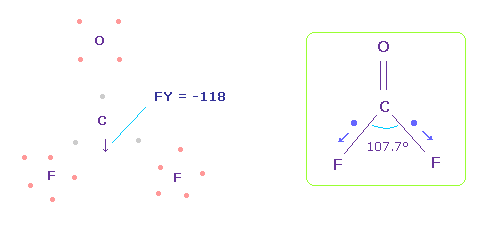
In this case, force acting on C nucleus becomes FY = -118.
This is almost zero, but is more attracted to fluorine, comparing with Fig.58.
This discrepancy is caused by neglecting strong electronegativity of fluorine.
Basically, carbon's electrons are strongly attracted to F and tend to go away from carbon.
As a result, electron density at F side is decreased, and bond angle is narrower.
So this FY = -118 is cancelled out by going-away electrons, and C nucleus becomes stable.
(Fig.61) O=CCl2 molecule.
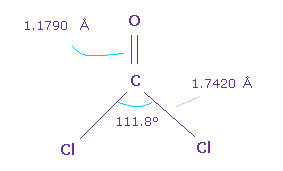
Next we think about O=CCl2 molecule.
The double bond length of C=O is 1.1790 Å, and Cl-C bond is 1.7420 Å
Cl-C-Cl angle is 111.8 degree, which is wider than F-C-F angle.
Because repulsive force between Cl-Cl positive nuclei is stronger than F-F.
In the same mechanism as in Fig.44, H tends to be attracted to oxygen, but Cl and F is repelled by oxygen.
So H-C-H angle (= 116.5 degree ) is wider than Cl-C-Cl angle (= 111.8 degree ).
After running the program, input "2" (= formaldehyde like ), and then input "2" ( O=CCl2 ), and press enter key.
(Fig.62) Forces acting on C nucleus.
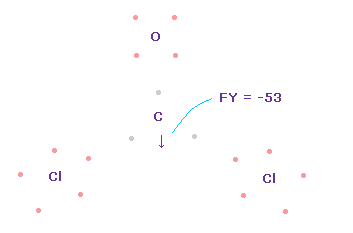
Like Fig.55 and Fig.56, we rotate O and C electrons to form double bonds.
And as I explain in Cl-CH3 and OCl2 molecule, we can suppose one of Cl electrons always points to C nucleus due to the long Cl-C bond length.
In this state, total forces acting on carbon nucleus ( atom 0 ) becomes FY = -53, which is almost zero and a good result.
In Fig.62, Cl-O-Cl angle is the experimental value of 111.8 degree, but corresponding carbon electron's e2-C-e3 angle remains to be original 109.45 degree.
(Fig.63) Widening carbon electron's angle from 109.45 to 111.8 degree.
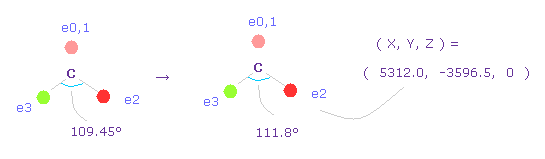
Considering attractive force of two chlorine nuclei, we widen the angles of carbon's valence electrons from 109.45 to 111.8 degree.
Input "0", click "electron" button, and input the coordinate of ( 5312.0, -3596.5, 0 ) into ele 2 textbox.
And input ( -5312.0, -3596.5, 0 ) into ele 3, and press enter key.
(Fig.64) Forces on C nucleus.
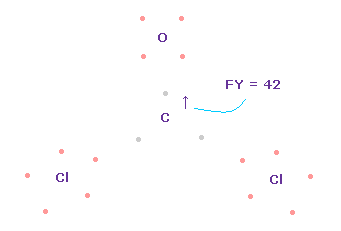
In this case, force acting on C nucleus becomes FY = +42.
This is good and almost zero, too.
Like formaldehyde case, also in O=CCl2 molecule, when e2-C-e3 angle is between 109.45 and 111.8 degree, total force acting on C nucleus becomes zero and stable.
This program can deal with various larger molecules.
About the detailed methods, see this page.

2013/5/10 updated. Feel free to link to this site.