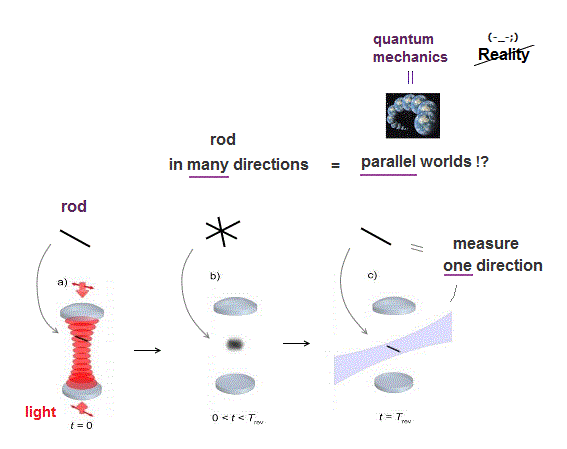
(Fig.1) Practical control of fragile neutral atomic qubits unstably trapped in laser light is impossible. ← Practical quantum computer is impossible.
Contrary to an incredible amount of hypes, neutral atomic qubits (= each atom's two energy levels are used as one qubit's 0 or 1 states ) unstably trapped in laser light lattice (= optical tweezers ) at cold temperature is useless for quantum computers.
It is impossible to control the positions and numbers of atoms (= atomic qubits ) trapped in laser light, which is too unreliable to use for practical quantum computers.
Atoms easily get lost and dissapper from the laser light, so physicists need to constantly load new atoms onto laser light randomly with the loading probability of just 50% ( this p.1-right, this p.1-left-2nd-paragraph ).
This 7th-paragraph says
"loading the atoms into the tweezers is a stochastic process—which means that the probability of each trap being occupied is 50%" ← error rate of 50% !
This 13th-paragraph says
"The time that the atoms stay in the optical tweezer is not that long. It is typically only a few milliseconds, and it is limited by the rate at which additional atoms are loaded into the trap." ← very unstable atomic qubits
This p.4-right-1st-paragraph says
"The result indicates that the probability of losing
a single atom across the entire array remains under 50%
during 100 ms" ← The error rate of 50% (= due to loss of atoms ) per 100 ms was too high !
Even by repeatedly loading new atoms onto optical lattice, the total number and positions of the loaded atoms are uncertain and fluctuating ( this p.5-Fig.4 ), which cannot be used for making reliable precise quantum computers.
Controlling and reading atomic qubits are impractical, taking much more time than other types of qubits such as superconducting qubits.
This 16~17th paragraphs say
"One reason the neutral-atom qubit isn't the front-runner in the quantum computer race is speed.... more than 1,000 times slower than a superconducting-qubit system..... they are finicky to operate.... researchers have yet to work out how to efficiently and rapidly operate more than a handful of neutral-atom qubits"
Just reading each atomic qubit 0 or 1 state by illuminating it with light is impractically slow and taking much more time (= ~ 80ms, this p.3-right-last-paragraph ).
So this neutral atomic qubit (= using excited Rydberg atomic state ) is about 10000 times slower than superconducting qubits (or classical computers ) used by IBM, Google.
↑ This Platform table shows superconducting qubit's speed 1.4 MHz is 10000 times faster than neutral atomic qubit (= Rydberg arrays )'s 170 Hz (= too slow to be practical ).
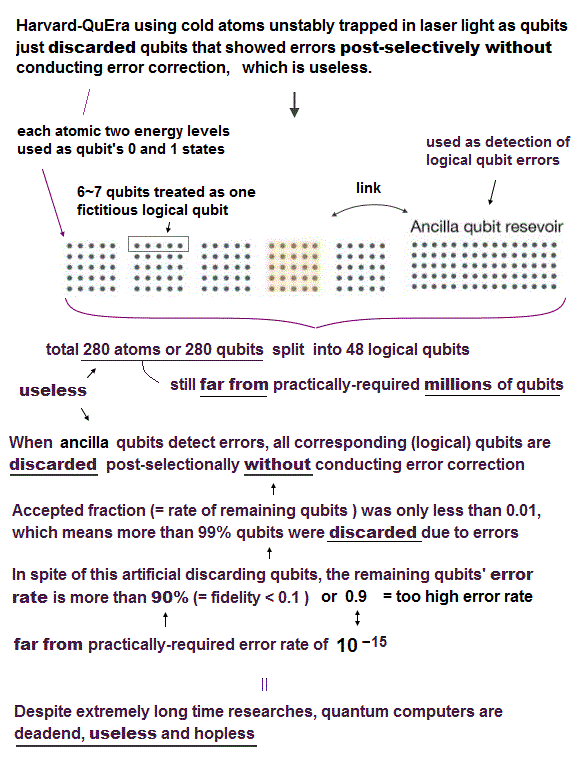
(Fig.2) Harvard-QuEra used only 280 unstable atoms divided into 4 or 48 (logical) qubits (= just 4 or 48 bitstring ) with extremely high error rates (= more than 90% error ) and No ability to correct errors. ← practical quantum computer is hopeless
Contrary to the overhyped news like "Key step toward reliable, game-changing quantum computing", Harvard-QuEra recent research published in Nature can never be a practical quantum computer.
They used only less than 280 cold atoms unstably trapped in laser light ( this 5th-paragraph ) as quantum bits or qubits: each atomic two energy levels were used as a (qu)bit's state 0 or 1 whose bit states could be changed by laser light ( this-middle neutral atom ).
But today's quantum computers are useless, too error-prone to give right answers.
They cannot use their 280 atoms as 280 qubits (= each qubit takes 0 or 1 states ), instead, they had to split 280 atomic (physical) qubits into just 4 or 48 (fictitious) logical qubits.
↑ So this Harvard-QuEra used only 4 or 48 bitstring (= each logical qubit can take only 0 or 1 state ), which is still Not a computer.
↑ Far from millions of qubits needed for a practical quantum computer ( this p.1-left-1st-paragraph ).
The point is today's quantum computers are too error-prone to correct their errors, because the operation of error correction itself increases the original errors instead of decreasing errors.
So physicists have No choice but to rely on illegitimate cheating called "post-selection" which just discards erroneous results or qubits without error correction.
↑ This Harvard's illegitimate post-selection approach cannot scale up quantum computers, because today's error-prone qubits so easily cause errors that almost all qubits must be discarded due to showing errors, which discarded qubits cannot be used for final calculated results.
This 5~6th-paragraphs say
"280 of these atoms were converted into qubits and entangled with the help of additional lasers, which resulted in the creation of 48 logical qubits."
"Instead of fixing mistakes that occur during computations (= instead of correcting errors ), the processor used by the Harvard team incorporates a post-processing error-detection phase. During this phase, erroneous outputs are discovered and discarded (= without error correction )"
The 4th-last paragraph of this site says
"What the Harvard team’s processor does, rather than correct errors during calculations, is add a post-processing error-detection phase wherein erroneous results are identified and rejected." ← illegitimately post-selection without error correction.
This 17-18th, 21th paragraphs say
"This isn't full error correction. What is happening in the paper is that the errors are corrected only after the calculation is done (= post-selection of results luckily avoiding errors )"
"But as the researchers got more stringent about rejecting measurements with indications of errors, the results got progressively cleaner. One measurement of accuracy rose from 0.16 to 0.62 (= still 84~38% error rates, even after discarding or rejecting erroneous results post-selectively.)"
"this isn't full error correction done while calculations are in progress, and QuEra is working on that. In addition, the algorithms used in these tests aren't useful in the sense that no commercial customer would pay to run them" ← useless and unable to correct errors.
This 33th, 35th paragraphs say
"they can preferentially reject measurement outcomes with errors, and therefore identify a subset of outcomes with lower errors. This approach is called post-selection, and while it can play a role in quantum error correction, it doesn't by itself solve the problem."
"Though there's still more to be done (← still useless )"
(Fig.3) Harvard-QuEra atomic qubits are too error-prone, useless, unable to correct errors.
↑ This research paper ↓
p.2-left-2nd~3rd-paragraphs say
"This architecture is implemented using
arrays of individual 87Rb atoms trapped in optical tweezers,"
"We use systems of up to
280 atomic qubits" ← up to 280 Rb atoms trapped in laser light were used as 280 qubits.
p.4-Fig.3 shows each logical qubit consists of 7 physical qubit (= Fig.3a ), and they tried to prepare 4 logical qubit's GHZ state = 4 qubits are all in the 0000 or 1111 states (= Fig.3e ).
↑ GHZ fidelity without postselecting on flags (= nFT = raw results ) was very bad = only 0.55 (= Fig.3c, nFT ), which means 45% error rates just for making 4 qubits the simple 0000 or 1111 bitstring (= GHZ ) states .
p.4-left-last-paragraph says "in which syndrome events (= ancilla qubits detecting errors ) most likely to have caused algorithmic failure are discarded (= discarding all results where ancilla qubits showed errors ).."
".. for example, discarding just 50% of the data improves GHZ fidelity to approximately 90%" ← Discarding 50% qubits or results (= accepted fraction was 0.5 ) due to showing errors without error correction improved GHZ fidelity to 0.9, as shown in Fig.3d or this Fig.
p.5-right-4th-paragraph says "To characterize the distribution overlap, we
use the cross-entropy benchmark (XEB)...
XEB = 1 corresponds to perfectly
reproducing the ideal distribution (= XEB = 1 is errorless or fidelity = 1 ) and XEB = 0 corresponds to the
uniform distribution, which occurs when circuits are overwhelmed by
noise (= XEB = 0 means 100% error rate or 0% fidelity )."
↑ XEB is equal to fidelity, so XEB = 0.35 means error rate of 65% ( this 10th-paragraph ).
p.5-right-5th-paragraph says "We obtain an XEB of approximately 0.1 for 48 logical qubits" ← 48 logical qubits showed 90% error rate (= XEB or fidelity was 0.1 ).
p.6-Fig.5e shows 48 logical qubits managed to get 0.1 XEB fidelity (= 90% error rate ) when the accepted fraction was less than 0.001 (= 90% error rate even after 99.9 % of the results or qubits were discarded due to showing errors ).
↑ These atomic qubits were useless, too error-prone (= actual error rate was more than 99.9% ), unable to correct errors (= instead, they just discarded or ignored erroneous results ).
↑ So even after 99.9% qubits or results were discarded postselectively without error correction, the remaining qubits showed 90% error rates, which is completely useless.
The 13-14th of this blog says
"With their IQP demonstration, they needed to postselect on the event that no errors occurred (!!), which happened about 0.1% of the time with their largest circuits (= which means 48 logical qubits showed 99.9% error rate, which must be discarded post-selectively )"
"They don't claim to have demonstrated quantum supremacy with their logical qubits—i.e., nothing that’s too hard to simulate using a classical computer." ← Quantum supremacy was fake.
Today's quantum error correction manipulating qubits is useless just increasing and worsening errors.
So all they can do is virtual error correction using classical computer's software without directly correcting erroneous qubits, as shown in this p.3-right-1st-paragraph says
"we can detect the presence of physical qubit
errors, decode (infer what error occurred) and correct the error simply
by applying a software ZL/XL correction24"
↑ This reference 24 paper's p.17-right-IX says
"The logical operators XˆL and ZˆL
that we have spent so much time discussing are Not actually implemented in the surface code hardware (= Not qubit hardware error correction )! These
operations are handled entirely by the classical control
software" ← No quantum error correction after all.
Feel free to link to this site.
